lqg

线性二次高斯 (LQG) 设计

语法

reg = lqg(sys,QXU,QWV) reg = lqg(sys,QXU,QWV,QI) reg = lqg(sys,QXU,QWV,QI,'1dof') reg = lqg(sys,QXU,QWV,QI,'2dof') reg = lqg(___,'current') [reg,info] = lqg(___)

说明

reg = lqg(sys,QXU,QWV) 根据被控对象的状态空间模型 sys 以及加权矩阵 QXU 和 QWV，计算最优线性二次高斯 (LQG) 调节器 reg。动态调节器 reg 使用测量值 y 生成控制信号 u，调节 y 使其在零值附近。使用正反馈将此调节器连接到被控对象输出 y。

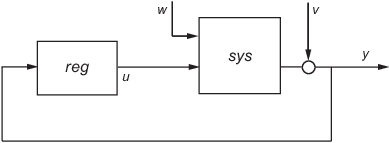
LQG 调节器最小化以下代价函数

$J = E {\lim_{τ \to \infty} \frac{1}{τ} \int_{0}^{τ} [x^{T}, u^{T}] Q_{x u} [\begin{matrix} x \\ u \end{matrix}] d t}$

但受限于以下被控对象方程

$\begin{matrix} d x / d t = A x + B u + w \\ y = C x + D u + v \end{matrix}$

其中过程噪声 w 和测量噪声 v 是具有协方差的高斯白噪声：

$E ([\begin{matrix} w \\ v \end{matrix}] \cdot [\begin{matrix} w' & v' \end{matrix}]) = Q W V$

reg = lqg(sys,QXU,QWV,QI) 使用设定点命令 r 和测量值 y 生成控制信号 u。reg 具有积分作用，以确保 y 跟踪命令 r。

LQG 伺服控制器最小化以下代价函数

$J = E {\lim_{τ \to \infty} \frac{1}{τ} \int_{0}^{τ} ([x^{T}, u^{T}] Q_{x u} [\begin{matrix} x \\ u \end{matrix}] + x_{i}^{T} Q_{i} x_{i}) d t}$

其中 x_i 是跟踪误差 r - y 的积分。对于 MIMO 系统，r、y 和 x_i 必须具有相同的长度。

reg = lqg(sys,QXU,QWV,QI,'1dof') 计算单自由度伺服控制器，其接受 e = r - y 而非 [r ; y] 作为输入。

reg = lqg(sys,QXU,QWV,QI,'2dof') 等效于 LQG(sys,QXU,QWV,QI)，并生成前面所示的二自由度伺服控制器。

reg = lqg(___,'current') 使用 "current" 卡尔曼估计器，在为离散时间系统计算 LQG 调节器时，该估计器使用 x[n|n] 作为状态估计值。

[reg,info] = lqg(___) 为以上任何语法在结构体 info 中返回控制器和估计器增益矩阵。例如，您可以使用控制器和估计器增益实现 Observer 形式的控制器。有关详细信息，请参阅算法。

示例

线性二次高斯 (LQG) 调节器和伺服控制器设计

此示例说明如何为以下系统设计线性二次高斯 (LQG) 调节器、单自由度 LQG 伺服控制器和二自由度 LQG 伺服控制器。

被控对象有三个状态 (x)、两个控制输入 (u)、三个随机输入 (w)、一个输出 (y)、输出的测量噪声 (v)，以及以下状态方程和测量方程：

$\begin{array}{l} \frac{d x}{d t} = A x + B u + w \\ y = C x + D u + v \end{array}$

其中

$\begin{array}{l} A = [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{matrix}] B = [\begin{matrix} 0.3 & 1 \\ 0 & 1 \\ - 0.3 & 0.9 \end{matrix}] \\ C = [\begin{matrix} 1.9 & 1.3 & 1 \end{matrix}] D = [\begin{matrix} 0.53 & - 0.61 \end{matrix}] \end{array}$

此系统具有以下噪声协方差数据：

$\begin{array}{l} Q_{n} = E (w w^{T}) = [\begin{matrix} 4 & 2 & 0 \\ 2 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] \\ R_{n} = E (v v^{T}) = 0.7 \end{array}$

对于调节器，使用以下代价函数来定义调节性能和控制力度之间的权衡：

$J (u) = \int_{0}^{\infty} (0.1 x^{T} x + u^{T} [\begin{matrix} 1 & 0 \\ 0 & 2 \end{matrix}] u) d t$

对于伺服控制器，使用以下代价函数来定义跟踪器性能和控制力度之间的权衡：

$J (u) = \int_{0}^{\infty} (0.1 x^{T} x + x_{i}^{2} + u^{T} [\begin{matrix} 1 & 0 \\ 0 & 2 \end{matrix}] u) d t$

要为此系统设计 LQG 控制器，请执行以下操作：

通过在 MATLAB 命令行窗口中键入以下命令创建状态空间系统：

A = [0 1 0;0 0 1;1 0 0];    
B = [0.3 1;0 1;-0.3 0.9];
C = [1.9 1.3 1];  
D = [0.53 -0.61];
sys = ss(A,B,C,D);

通过键入以下命令定义噪声协方差数据和加权矩阵：

nx = 3;    %Number of states
ny = 1;    %Number of outputs
Qn = [4 2 0; 2 1 0; 0 0 1];
Rn = 0.7;
R = [1 0;0 2]
QXU = blkdiag(0.1*eye(nx),R);
QWV = blkdiag(Qn,Rn);
QI = eye(ny);

通过键入以下命令构建 LQG 调节器：

KLQG = lqg(sys,QXU,QWV)

此命令返回以下 LQG 调节器：

A = 
           x1_e    x2_e    x3_e
   x1_e  -6.212  -3.814  -4.136
   x2_e  -4.038  -3.196  -1.791
   x3_e  -1.418  -1.973  -1.766
 
B = 
             y1
   x1_e   2.365
   x2_e   1.432
   x3_e  0.7684
 
C = 
            x1_e       x2_e       x3_e
   u1   -0.02904  0.0008272     0.0303
   u2    -0.7147    -0.7115    -0.7132
 
D = 
       y1
   u1   0
   u2   0
 
Input groups:              
       Name        Channels
    Measurement       1    
                           
Output groups:             
      Name      Channels   
    Controls      1,2      
                           
Continuous-time model.

通过键入以下命令构建单自由度 LQG 伺服控制器：

KLQG1 = lqg(sys,QXU,QWV,QI,'1dof')

此命令返回以下 LQG 伺服控制器：

A = 
           x1_e    x2_e    x3_e     xi1
   x1_e  -7.626  -5.068  -4.891  0.9018
   x2_e  -5.108  -4.146  -2.362  0.6762
   x3_e  -2.121  -2.604  -2.141  0.4088
   xi1        0       0       0       0
 
B = 
              e1
   x1_e   -2.365
   x2_e   -1.432
   x3_e  -0.7684
   xi1         1
 
C = 
          x1_e     x2_e     x3_e      xi1
   u1  -0.5388  -0.4173  -0.2481   0.5578
   u2   -1.492   -1.388   -1.131   0.5869
 
D = 
       e1
   u1   0
   u2   0
 
Input groups:           
    Name     Channels   
    Error       1       
                        
Output groups:          
      Name      Channels
    Controls      1,2   
                        
Continuous-time model.

通过键入以下命令构建二自由度 LQG 伺服控制器：

KLQG2 = lqg(sys,QXU,QWV,QI,'2dof')

此命令返回以下 LQG 伺服控制器：

A = 
           x1_e    x2_e    x3_e     xi1
   x1_e  -7.626  -5.068  -4.891  0.9018
   x2_e  -5.108  -4.146  -2.362  0.6762
   x3_e  -2.121  -2.604  -2.141  0.4088
   xi1        0       0       0       0
 
B = 
             r1      y1
   x1_e       0   2.365
   x2_e       0   1.432
   x3_e       0  0.7684
   xi1        1      -1
 
C = 
          x1_e     x2_e     x3_e      xi1
   u1  -0.5388  -0.4173  -0.2481   0.5578
   u2   -1.492   -1.388   -1.131   0.5869
 
D = 
       r1  y1
   u1   0   0
   u2   0   0
 
Input groups:              
       Name        Channels
     Setpoint         1    
    Measurement       2    
                           
Output groups:             
      Name      Channels   
    Controls      1,2      
                           
Continuous-time model.

提示

lqg 可用于连续时间被控对象，也可用于离散时间被控对象。在离散时间中，lqg 默认使用 x[n|n-1] 作为其状态估计值。要使用 x[n|n] 作为状态估计值并计算最优 LQG 控制器，请使用 'current' 输入参量。有关状态估计器的详细信息，请参阅 kalman。
为了计算 LQG 调节器，lqg 使用命令 lqr 和 kalman。为了计算伺服控制器，lqg 使用命令 lqi 和 kalman。
如果您希望更灵活地设计调节器，可以使用 lqr、kalman 和 lqgreg 命令。如果您希望更灵活地设计伺服控制器，可以使用 lqi、kalman 和 lqgtrack 命令。有关使用这些命令以及如何确定何时使用它们的详细信息，请参阅用于调节的线性二次高斯 (LQG) 设计和具有积分作用的伺服控制器的线性二次高斯 (LQG) 设计。

算法

控制器方程为：

对于连续时间：
$\begin{matrix} d x_{e} = A x_{e} + B u + L (y - C x_{e} - D u) \\ u = - K_{x} x_{e} - K_{i} x_{i} \end{matrix}$
对于离散时间：
$x [n + 1 | n] = A x [n | n - 1] + B u [n] + L (y [n] - C x [n | n - 1] - D u [n])$
- 延迟估计器：
  $u [n] = - K_{x} x [n | n - 1] - K_{i} x_{i} [n]$
- 当前估计器：
  $\begin{matrix} u [n] = - K_{x} x [n | n] - K_{i} x_{i} [n] - K_{w} w [n | n] \\ = - K_{x} x [n | n - 1] - K_{i} x_{i} [n] - (K_{x} M_{x} + K_{w} M_{w}) y_{i n n} [n] \end{matrix}$
  $y_{i n n} [n] = y [n] - C x [n | n - 1] - D u [n]$

其中，

A、B、C 和 D 是 LQG 调节器 reg 的状态空间矩阵。
x_i 是跟踪误差 r - y 的积分。
K_x、K_w、K_i、L、M_x 和 M_w 是在 info 中返回的控制器和估计器增益矩阵。

版本历史记录

在 R2006a 之前推出

另请参阅

lqr | lqi | kalman | lqry | ss | care | dare