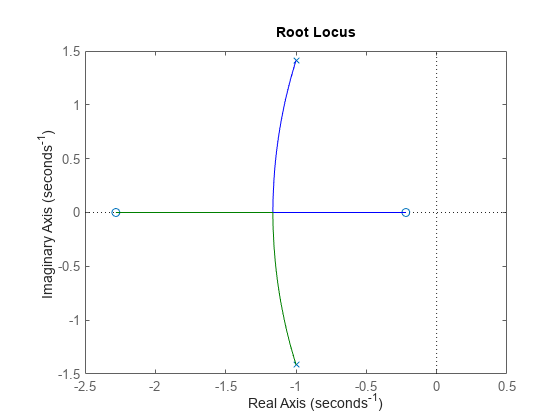
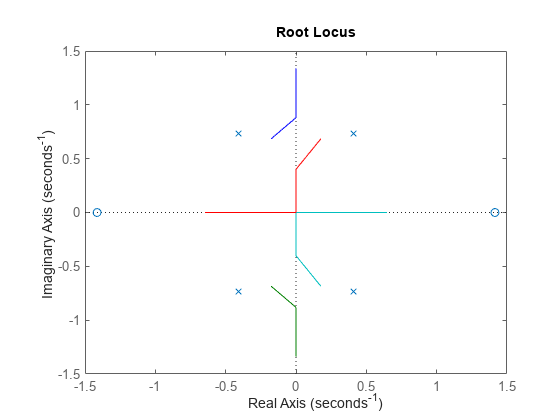
rlocus
动态系统的根轨迹
说明
rlocus(___) 使用所有先前输入参量组合的默认绘图选项绘制 SISO 模型 sys 的根轨迹。如需更多绘图自定义选项,请使用 rlocusplot。
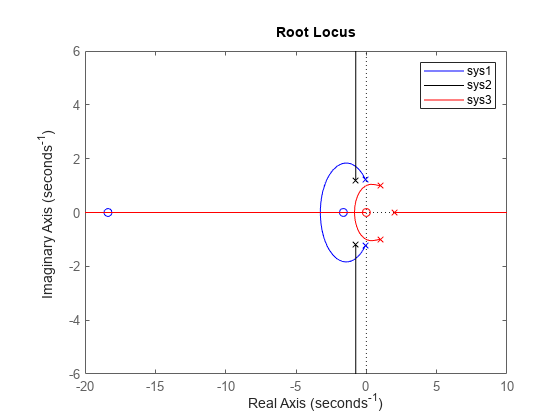
要在同一图上绘制多个动态系统的根轨迹,您可以将
sys指定为以逗号分隔的模型列表。例如,rlocus(sys1,sys2,sys3)在同一图上绘制三个模型的根轨迹。要为图中的每个系统分别指定一种颜色、线型和标记,请为每个系统指定
LineSpec值。例如,rlocus(sys1,LineSpec1,sys2,LineSpec2)绘制两个模型并指定它们的绘图样式。有关指定LineSpec值的详细信息,请参阅rlocusplot。
示例
输入参数
输出参量
提示
有关根轨迹绘制的交互式方法,请参阅控制系统设计器。
对于用于自定义根轨迹图外观的其他选项,请使用
rlocusplot。使用
rlocus创建的绘图不支持以字符串数组或字符向量元胞数组形式指定的多行标题或标签。要指定多行标题和标签,请使用包含newline字符的单个字符串。rlocus(sys) title("first line" + newline + "second line");
算法
动态系统的根轨迹包含作为反馈增益 k 的函数的闭环极点轨迹(假设负反馈)。根轨迹用于研究不同反馈增益对闭环极点位置的影响。反过来,这些位置提供有关时间和频率响应的间接信息。
您可以使用 rlocus 通过设置 sys 计算以下任何负反馈环的根轨迹图,如下图所示。
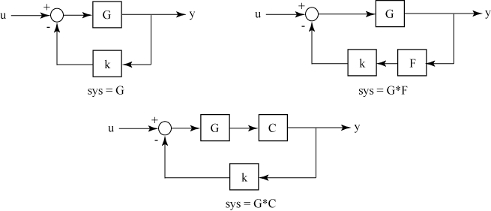
例如,如果 sys 是由下式表示的传递函数:
则闭环极点是下式的根:
根轨迹图描绘随着反馈增益 k 从 0 变化到无穷大时闭环极点的轨迹。