margin
增益裕度、相位裕度和穿越频率
语法
说明
裕度图
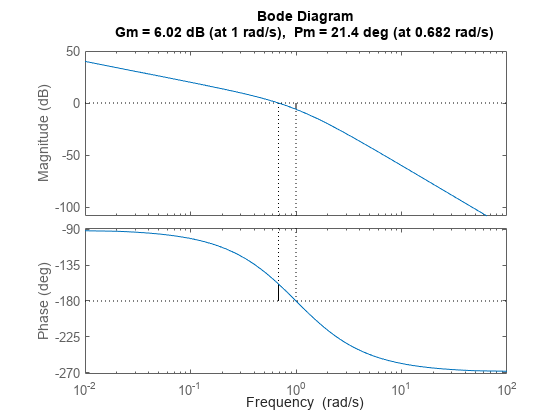
margin( 在屏幕上绘制 sys)sys 的波特响应图，并在图上指示增益裕度和相位裕度。增益裕度在图上以 dB 为单位表示。
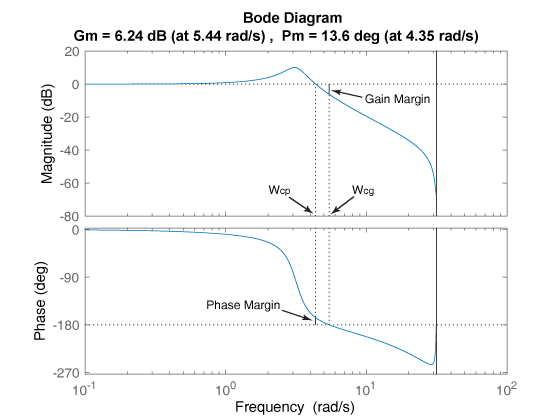
垂直实线标记增益裕度和相位裕度。垂直虚线指示 Wcp（测量相位裕度的频率）和 Wcg（测量增益裕度的频率）的位置。图标题中包括增益裕度和相位裕度的幅值和位置。
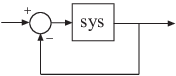
系统的 Gm 和 Pm 指示对 sys 应用单位负反馈所形成的闭环系统的相对稳定性，如下图所示。
Gm 是使环路增益在相位角为 –180°（以 360° 为模）的频率 Wcg 下达到单位 1 所需的增益变化量。换句话说，如果 g 是 –180° 相位频率下的增益，则增益裕度为 1/g。同样，相位裕度是当环路增益为 1.0 时，响应相位与 –180° 之间的差值。幅值为 1.0 的频率 Wcp 称为单位增益频率或增益穿越频率。当 sys 有多个穿越时，margin 指示增益裕度最接近 0 dB 且相位裕度最接近 0° 时的频率。
通常，3 或更大的增益裕度与介于 30° 和 60° 之间的相位裕度相结合，可以在带宽和稳定性之间实现合理的权衡。然而，在一些多变量系统中，如果有更小的增益和相位变化，在不同的频率下可能会失去稳定性。对于此类系统，磁盘裕度的概念提供了对真实增益裕度和相位裕度的更可靠估计。有关磁盘裕度的详细信息，请参阅 diskmargin (Robust Control Toolbox)。
裕度值
示例
对于此示例，请创建一个连续传递函数。
sys = tf(1,[1 2 1 0])
sys =
1
---------------
s^3 + 2 s^2 + s
Continuous-time transfer function.
Model Properties
以图形方式显示增益裕度和相位裕度。
margin(sys)
标题中显示的增益裕度 (6.02 dB) 和相位裕度（21.4 度）用垂直实线标记。垂直虚线指示 Wcg（测量增益裕度的频率）和 Wcp（测量相位裕度的频率）的位置。
对于此示例，请创建一个离散时间传递函数。
sys = tf([0.04798 0.0464],[1 -1.81 0.9048],0.1)
sys = 0.04798 z + 0.0464 --------------------- z^2 - 1.81 z + 0.9048 Sample time: 0.1 seconds Discrete-time transfer function. Model Properties
计算增益裕度、相位裕度和频率。
[Gm,Pm,Wcg,Wcp] = margin(sys)
Gm = 2.0519
Pm = 13.5711
Wcg = 5.4376
Wcp = 4.3544
结果表明，在 5.43 弧度/秒的相位穿越频率下，增益变化超过 2.05 (6.24 dB) 将导致系统不稳定。同样，在 4.35 弧度/秒的增益穿越频率下，相位变化超过 13.57 度将导致系统失去稳定性。
自 R2024a 起
在某些应用中，您可能希望计算特定频率范围内的稳定裕度，而忽略该范围外的动态特性。例如，以如下系统为例，该系统同时具有相对低频和相对高频下的动态特性。
sys = tf(5,[1 1 10]) + tf(5e3,[1 20 1e4]); damp(sys)
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
-5.00e-01 + 3.12e+00i 1.58e-01 3.16e+00 2.00e+00
-5.00e-01 - 3.12e+00i 1.58e-01 3.16e+00 2.00e+00
-1.00e+01 + 9.95e+01i 1.00e-01 1.00e+02 1.00e-01
-1.00e+01 - 9.95e+01i 1.00e-01 1.00e+02 1.00e-01
闭环系统 CL = feedback(sys,1) 在低频下对扰动的稳定性与高频下的稳定性不同。要查看差异，请使用 Focus 选项。首先，检查低于 10 弧度/秒的裕度。
[GmL,PmL,WcgL,WcpL] = margin(sys,Focus=[0 10])
GmL = Inf
PmL = 80.9920
WcgL = NaN
WcpL = 3.5137
检查大约 10 弧度/秒的裕度。
[GmH,PmH,WcgH,WcpH] = margin(sys,Focus=[10 Inf])
GmH = Inf
PmH = 28.6437
WcgH = Inf
WcpH = 119.9618
对于此示例，请加载开环系统的频率响应数据，包括在 w 中的频率下测得的幅值 (m) 和相位值 (p)。
load('openLoopFRD.mat','p','m','w');
计算增益裕度和相位裕度。
[Gm,Pm,Wcg,Wcp] = margin(m,p,w)
Gm = 0.6249
Pm = 48.9853
Wcg = 1.2732
Wcp = 1.5197
对于此示例，请加载 invertedPendulumArray.mat，其包含一个由倒立摆模型组成的 3×3 数组。摆的质量随着您沿 sys 的单个列在模型间移动而变化，摆的长度随着您沿单个行移动而变化。所用的质量值分别为 100g、200g 和 300g，所用的摆长度分别为 3m、2m 和 1m。
load('invertedPendulumArray.mat','sys'); size(sys)
3x3 array of transfer functions. Each model has 1 outputs and 1 inputs.
求数组中所有模型的增益裕度和相位裕度。
[Gm,Pm] = margin(sys)
Gm = 3×3
0.9800 0.9800 0.9800
0.9800 0.9800 0.9800
0.9800 0.9800 0.9800
Pm = 3×3
-11.3798 -11.4118 -11.4433
-11.4059 -11.4296 -11.4532
-11.4228 -11.4410 -11.4592
margin 返回两个数组 Gm 和 Pm，其中每个条目是 sys 中对应条目的增益裕度值和相位裕度值。例如，摆重量为 100g、长度为 2m 的模型的增益裕度和相位裕度分别为 Gm(1,2) 和 Pm(1,2)。
输入参数
输出参量
提示
当您使用
margin(mag,phase,w)时，margin依赖于插值来逼近裕度，这通常会产生不太准确的结果。例如，如果w范围内没有穿越 0 dB 的频率点，则margin返回Inf的相位裕度。因此，如果您有一个分析模型sys，则使用[Gm,Pm,Wcg,Wcp] = margin(sys)是获得裕度的更可靠方法。如果您有 Robust Control Toolbox™ 软件，则可以使用
diskmargin(Robust Control Toolbox) 来计算基于磁盘的裕度，这些裕度定义了反馈环保持稳定的“安全”增益和相位变化范围。
