评估增益裕度和相位裕度

反馈环的稳定性

稳定性通常意味着所有内部信号都保持有界。稳定性是控制系统的一项标准要求，它可以避免失控和设备损坏。对于线性反馈系统，可以通过查看闭环传递函数的极点来评估稳定性。例如，假设有以下 SISO 反馈环：

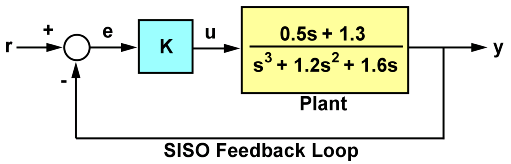
图 1：SISO 反馈环。

对于单位环路增益 k，您可以使用以下公式计算闭环传递函数 T：

G = tf([.5 1.3],[1 1.2  1.6 0]);
T = feedback(G,1);

要获得 T 的极点，请输入：

pole(T)

ans =

  -0.2305 + 1.3062i
  -0.2305 - 1.3062i
  -0.7389 + 0.0000i

k=1 时的反馈环是稳定的，因为所有极点都具有负实部。

怎样才算稳定？

通过检查闭环极点，我们可以对稳定性进行二元评估。实际上，了解稳健性有多强（或多弱）更有用。稳健性的一个标志是在失去稳定性之前环路增益会变化多少。您可以使用根轨迹图来估计环路处于稳定状态时的 k 值的范围：

rlocus(G)

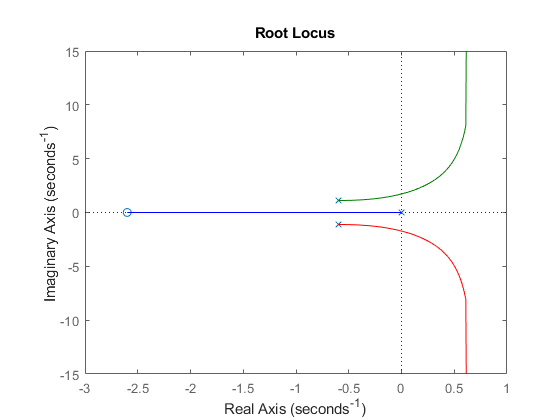
点击根轨迹与 y 轴相交的点可以发现，在以下增益值范围内，此反馈环是稳定的：

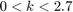
这个范围表明，k=1 时，此反馈环在环路增益增加 270% 之前都是稳定的。

增益裕度和相位裕度

环路增益的变化只是稳健性的一个方面。一般情况下，如果被控对象建模不完善，则意味着增益和相位都无法精确得知。由于建模误差在增益穿越频率（开环增益为 0dB 的频率）附近造成的影响最为严重，因此在此频率下可以容忍多大的相位变化也很重要。

相位裕度衡量在增益穿越频率下环路失去稳定性所需要的相位变化量。类似地，增益裕度衡量在相位穿越频率下环路失去稳定性所需要的相对增益变化量。这两个数值共同给出闭环稳定性的安全裕度估计值。稳定裕度越小，稳定性就越脆弱。

您可以在波特图上显示增益和相位裕度，如下所示。首先创建波特图：

bode(G), grid

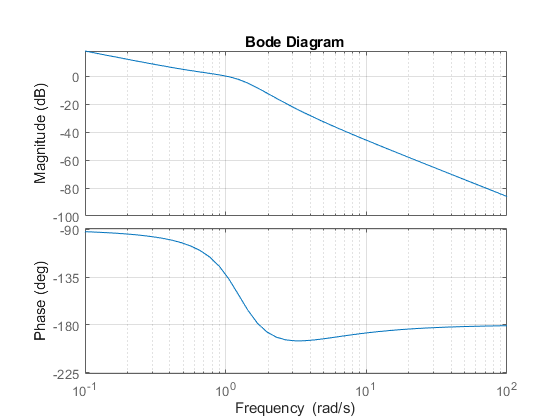
然后，右键点击该图并选择特征 -> 最小稳定裕度子菜单。最后，点击蓝色圆点标记。得到的绘图如下所示：

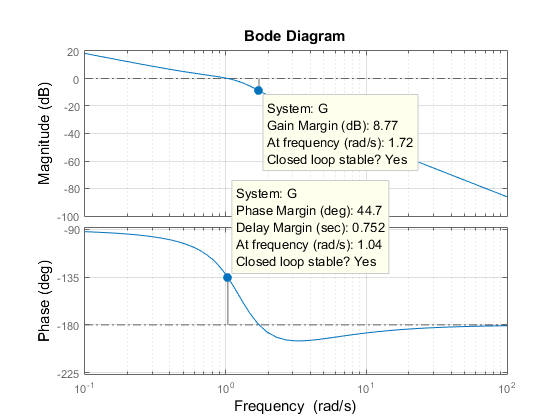
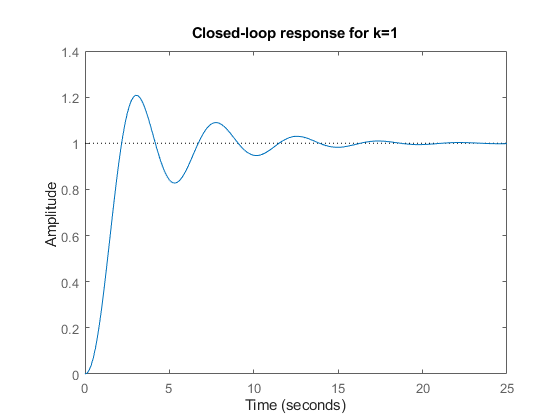
这表明增益裕度约为 9 dB，相位裕度约为 45 度。相应的闭环阶跃响应表现出约 20% 的过冲和一些振荡。

step(T), title('Closed-loop response for k=1')

如果我们将增益增加到 k=2，稳定裕度将降低到

[Gm,Pm] = margin(2*G);
GmdB = 20*log10(Gm)   % gain margin in dB
Pm  % phase margin in degrees

GmdB =

    2.7435


Pm =

    8.6328

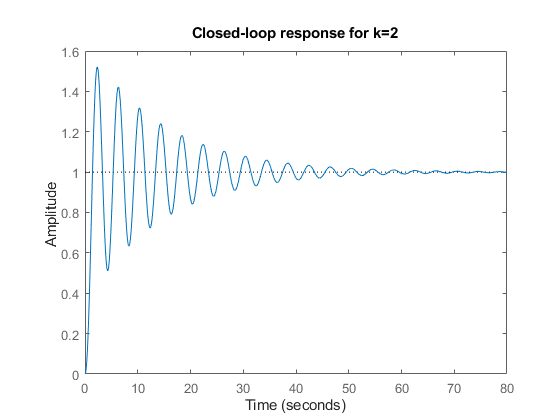
并且闭环响应具有低阻尼振荡，这是接近不稳定的迹象。

step(feedback(2*G,1)), title('Closed-loop response for k=2')

具有多个增益或相位穿越频率的系统

一些系统具有多个增益穿越或相位穿越频率，这会导致多个增益或相位裕度值。例如，假设有以下反馈环：

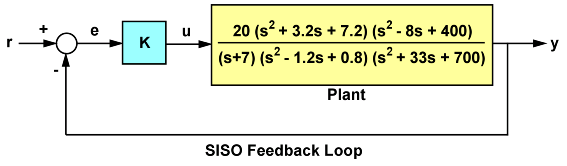
图 2：具有多个相位穿越频率的反馈环

k=1 时的闭环响应是稳定的：

G = tf(20,[1 7]) * tf([1 3.2 7.2],[1 -1.2 0.8]) * tf([1 -8 400],[1 33 700]);
T = feedback(G,1);
step(T), title('Closed-loop response for k=1')

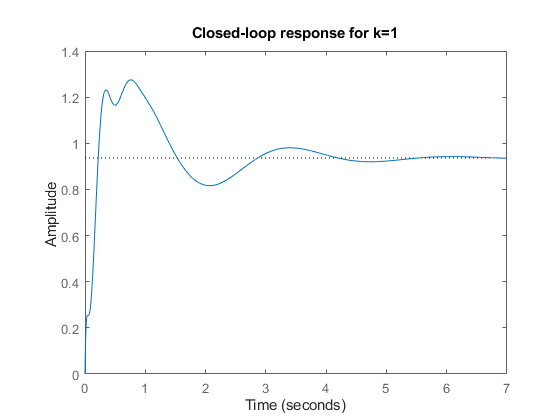
为了评估此环路的稳定鲁棒性，请绘制其波特响应图：

bode(G), grid

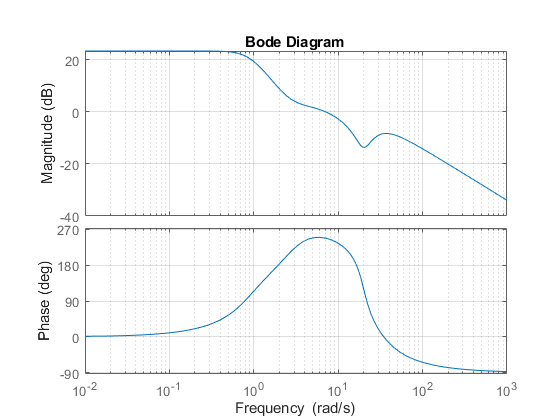
然后，右键点击该图并选择特征 -> 所有稳定裕度子菜单，以显示所有穿越频率和相关的稳定裕度。得到的绘图如下所示。

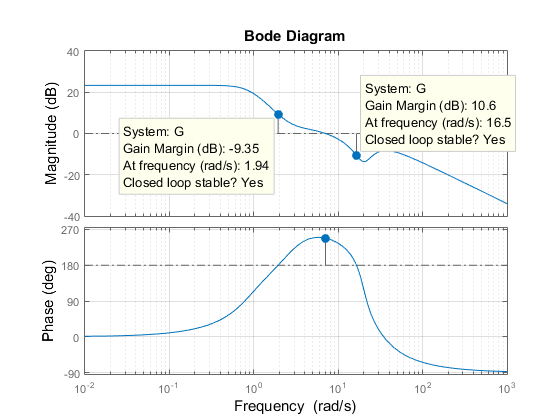
请注意，存在两个 180 度相位穿越频率，对应的增益裕度分别为 -9.35 dB 和 +10.6 dB。负增益裕度表示降低增益会失去稳定性，而正增益裕度表示增加增益会失去稳定性。通过绘制围绕 k=1 进行正负 6 dB 增益变化的闭环阶跃响应可以证实这一点：

k1 = 2;     T1 = feedback(G*k1,1);
k2 = 1/2;   T2 = feedback(G*k2,1);
step(T,'b',T1,'r',T2,'g',12),
legend('k = 1','k = 2','k = 0.5')

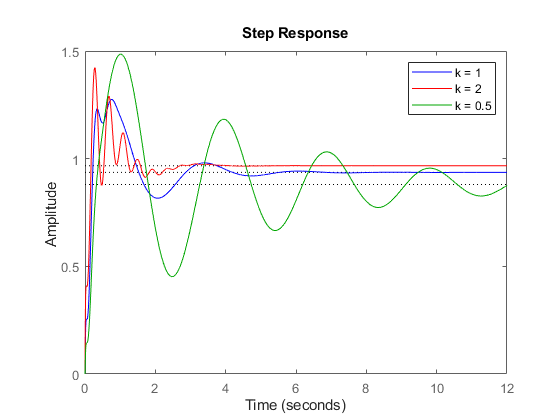
该图显示，对于较小和较大的增益值，振荡都有所增加。

您可以使用 allmargin 命令来计算所有稳定裕度。请注意，增益裕度以增益比表示，而不是以 dB 表示。使用 mag2db 将值转换为 dB。

m = allmargin(G)

GainMargins_dB = mag2db(m.GainMargin)

m = 

  struct with fields:

     GainMargin: [0.3408 3.3920]
    GMFrequency: [1.9421 16.4807]
    PhaseMargin: 68.1140
    PMFrequency: 7.0776
    DelayMargin: 0.1680
    DMFrequency: 7.0776
         Stable: 1


GainMargins_dB =

   -9.3510   10.6091