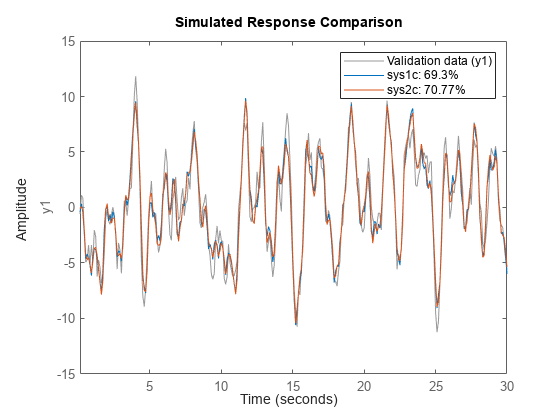
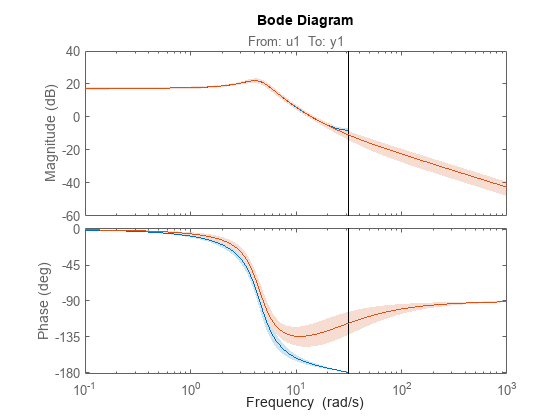
d2c
将模型从离散时间转换为连续时间
说明
示例
输入参数
输出参量
参考
[1] Franklin, G.F., Powell,D.J., and Workman, M.L., Digital Control of Dynamic Systems (3rd Edition), Prentice Hall, 1997.
[2] Kollár, I., G.F. Franklin, and R. Pintelon, "On the Equivalence of z-domain and s-domain Models in System Identification," Proceedings of the IEEE® Instrumentation and Measurement Technology Conference, Brussels, Belgium, June, 1996, Vol. 1, pp. 14-19.
版本历史记录
在 R2006a 之前推出
另请参阅
d2cOptions | c2d | translatecov (System Identification Toolbox) | logm | 转换模型速率