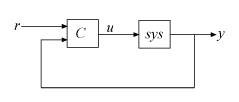
pidtune
线性被控对象模型的 PID 调节算法
语法
说明
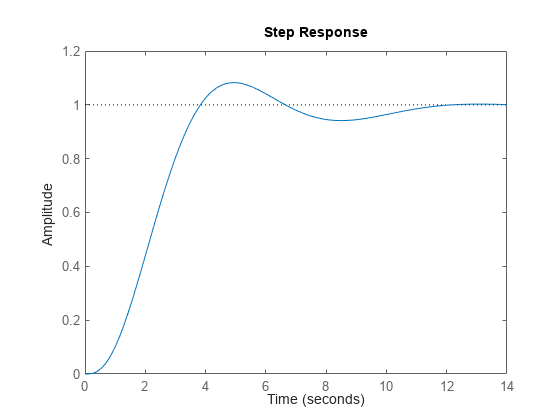
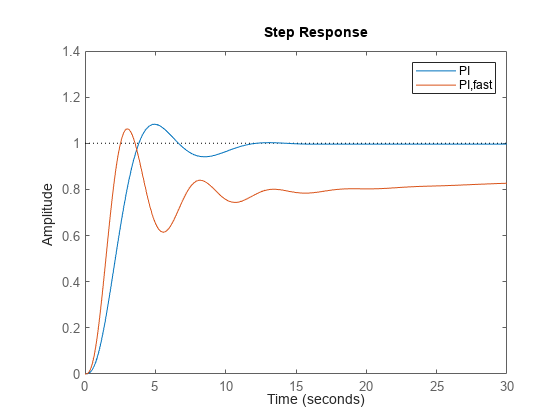
示例
此示例说明如何为由下式给出的被控对象设计 PID 控制器：
首先，创建一个被控对象模型，并为其设计简单的 PI 控制器。
sys = zpk([],[-1 -1 -1],1);
[C_pi,info] = pidtune(sys,'PI')C_pi =
1
Kp + Ki * ---
s
with Kp = 1.14, Ki = 0.454
Continuous-time PI controller in parallel form.
Model Properties
info = struct with fields:
Stable: 1
CrossoverFrequency: 0.5205
PhaseMargin: 60.0000
C_pi 是表示 PI 控制器的 pid 控制器对象。info 的字段显示，调节算法选择约 0.52 弧度/秒的开环穿越频率。
检查受控系统的闭环阶跃响应（参考跟踪）。
T_pi = feedback(C_pi*sys, 1); step(T_pi)
为了改进响应时间，您可以设置比 pidtune 自动选择的结果（即 0.52）更高的目标穿越频率。将穿越频率提高到 1.0。
[C_pi_fast,info] = pidtune(sys,'PI',1.0)C_pi_fast =
1
Kp + Ki * ---
s
with Kp = 2.83, Ki = 0.0495
Continuous-time PI controller in parallel form.
Model Properties
info = struct with fields:
Stable: 1
CrossoverFrequency: 1
PhaseMargin: 43.9973
新控制器可实现更高的穿越频率，但代价是相位裕度降低。
比较两个控制器的闭环阶跃响应。
T_pi_fast = feedback(C_pi_fast*sys,1); step(T_pi,T_pi_fast)
axis([0 30 0 1.4])
legend('PI','PI,fast')
性能下降的原因是 PI 控制器没有足够的自由度在 1.0 弧度/秒的穿越频率下实现良好的相位裕度。增加导数作用可以改进响应。
为 Gc 设计 PIDF 控制器，目标穿越频率为 1.0 弧度/秒。
[C_pidf_fast,info] = pidtune(sys,'PIDF',1.0)信息字段显示，控制器中的导数作用允许调节算法设计一个更激进的控制器，以实现具有良好相位裕度的目标穿越频率。
比较快速 PI 和 PIDF 控制器的闭环阶跃响应和抗扰。
T_pidf_fast = feedback(C_pidf_fast*sys,1); step(T_pi_fast, T_pidf_fast); axis([0 30 0 1.4]); legend('PI,fast','PIDF,fast');
您可以将受控系统的输入（负载）抗扰与快速 PI 和 PIDF 控制器进行比较。为此，绘制从被控对象输入到被控对象输出的闭环传递函数的响应。
S_pi_fast = feedback(sys,C_pi_fast); S_pidf_fast = feedback(sys,C_pidf_fast); step(S_pi_fast,S_pidf_fast); axis([0 50 0 0.4]); legend('PI,fast','PIDF,fast');
上图表明，PIDF 控制器还展示了更快的抗扰能力。
为以下被控对象设计标准型 PID 控制器。
要设计标准型控制器，需将标准型控制器作为 pidtune 的 C0 参量传入。
sys = zpk([],[-1 -1 -1],1); C0 = pidstd(1,1,1); C = pidtune(sys,C0)
C =
1 1
Kp * (1 + ---- * --- + Td * s)
Ti s
with Kp = 2.18, Ti = 2.57, Td = 0.642
Continuous-time PID controller in standard form
Model Properties
使用指定方法离散化积分器，进而设计离散时间 PI 控制器。
如果被控对象为离散时间模型，pidtune 会自动返回采用默认前向欧拉积分法的离散时间控制器。要指定其他积分方法，可使用 pid 或 pidstd 创建具有所需积分方法的离散时间控制器。
sys = c2d(tf([1 1],[1 5 6]),0.1); C0 = pid(1,1,'Ts',0.1,'IFormula','BackwardEuler'); C = pidtune(sys,C0)
C =
Ts*z
Kp + Ki * ------
z-1
with Kp = -0.0658, Ki = 1.32, Ts = 0.1
Sample time: 0.1 seconds
Discrete-time PI controller in parallel form.
Model Properties
将 C0 作为输入时，pidtune 设计的控制器 C 会与 C0 具有相同的形式、类型和离散化方法。显示结果表明，C 的积分项采用后向欧拉积分法。
指定梯形积分器，并对所得控制器进行比较。
C0_tr = pid(1,1,'Ts',0.1,'IFormula','Trapezoidal'); Ctr = pidtune(sys,C0_tr)
Ctr =
Ts*(z+1)
Ki * --------
2*(z-1)
with Ki = 1.32, Ts = 0.1
Sample time: 0.1 seconds
Discrete-time I-only controller.
Model Properties
为以下传递函数表示的被控对象设计二自由度 PID 控制器：
使用目标带宽 1.5 弧度/秒。
wc = 1.5;
G = tf(1,[1 0.5 0.1]);
C2 = pidtune(G,'PID2',wc)C2 =
1
u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
s
with Kp = 1.26, Ki = 0.255, Kd = 1.38, b = 0.665, c = 0
Continuous-time 2-DOF PID controller in parallel form.
Model Properties
使用类型 'PID2' 会导致 pidtune 生成一个二自由度控制器，表示为 pid2 对象。显示画面确认了此结果。显示画面还说明 pidtune 可调节所有控制器系数，包括设定值权重 b 和 c，以平衡性能和稳健性。
输入参数
输出参量
提示
默认情况下，带有
type输入的pidtune会返回并联型pid控制器。要设计标准型控制器，请使用pidstd控制器作为输入参量C0。有关并联型和标准型控制器的详细信息，请参阅pid和pidstd参考页。有关实时编辑器中的交互式 PID 调节，请参阅调节 PID 控制器实时编辑器任务。此任务可以交互方式设计 PID 控制器，并为实时脚本自动生成 MATLAB® 代码。
算法
有关 MathWorks® PID 调节算法的信息，请参阅 PID 调节算法。
替代功能
有关实时编辑器中的交互式 PID 调节，请参阅调节 PID 控制器实时编辑器任务。此任务可以交互方式设计 PID 控制器，并为实时脚本自动生成 MATLAB 代码。有关示例，请参阅PID Controller Design in the Live Editor
对于独立 App 中的交互式 PID 调节，请使用 PID 调节器。有关使用该 App 设计控制器的示例，请参阅用于快速参考跟踪的 PID 控制器设计。
参考
[1] Åström, Karl J., and Tore Hägglund. Advanced PID Control. Research Triangle Park, NC: ISA-The Instrumentation, Systems, and Automation Society, 2006.
版本历史记录
在 R2010b 中推出
