pidstd2

2-DOF PID controller in standard form

Description

Use pidstd2 to create standard-form, two-degree-of-freedom (2-DOF) proportional-integral-derivative (PID) controller model objects, or to convert dynamic system models to standard 2-DOF PID controller form.

2-DOF PID controllers include setpoint weighting on the proportional and derivative terms. A 2-DOF PID controller can achieve fast disturbance rejection without significant increase of overshoot in setpoint tracking. 2-DOF PID controllers are also useful to mitigate the influence of changes in the reference signal on the control signal. The following illustration shows a typical control architecture using a 2-DOF PID controller.

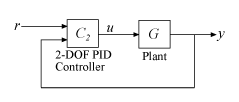
The pidstd2 controller model object can represent standard-form PID controllers in continuous time or discrete time.

Continuous time — $u = K_{p} [(b r - y) + \frac{1}{T_{i} s} (r - y) + \frac{T_{d} s}{\frac{T_{d}}{N} s + 1} (c r - y)]$
Discrete time — $u = K_{p} [(b r - y) + \frac{1}{T_{i}} I F (z) (r - y) + \frac{T_{d}}{\frac{T_{d}}{N} + D F (z)} (c r - y)]$

Here:

b is the setpoint weighting on the proportional term.
c is the setpoint weighting on the derivative term.
K_p is the proportional gain.
T_i is the integral time.
T_d is the derivative time.
N is the first-order derivative filter divisor.
IF(z) is the integrator method for computing the integral in the discrete-time controller.
DF(z) is the integrator method for computing the derivative filter in the discrete-time controller.

You can then combine this object with other components of a control architecture, such as the plant, actuators, and sensors to represent your control system. For more information, see Control System Modeling with Model Objects.

You can create a PID controller model object by either specifying the controller parameters directly, or by converting a model of another type (such as a transfer function model tf) to PID controller form.

You can also use pidstd2 to create generalized state-space (genss) models or uncertain state-space (uss (Robust Control Toolbox)) models.

Creation

You can obtain pidstd2 controller models in one of the following ways.

Create a model using the pidstd2 function.
Use the pidtune function to tune PID controllers for a plant model. Specify a baseline standard-form 2-DOF PID controller type using the C0 argument of the pidtune function. For example:
```
sys = zpk([],[-1 -1 -1],1);
C0 = pidstd2(1,1,1);
C2 = pidtune(sys,C0)
```
Interactively tune the PID controller for a plant model using:
- The Tune PID Controller Live Editor task.
- The PID Tuner app.

Syntax

C2 = pidstd2(Kp,Ti,Td,N,b,c)

C2 = pidstd2(Kp,Ti,Td,N,b,c,Ts)

C2 = pidstd2(___,Name,Value)

C2 = pidstd2

C2 = pidstd2(sys)

Description

C2 = pidstd2(Kp,Ti,Td,N,b,c) creates a continuous-time 2-DOF standard-form PID controller model and sets the properties Kp, Ti, Td, and N. The remaining properties have default values.

example

C2 = pidstd2(Kp,Ti,Td,N,b,c,Ts) creates a discrete-time 2-DOF PID controller model with sample time Ts.

example

C2 = pidstd2(___,Name,Value) sets properties of the pidstd2 controller object specified using one or more Name,Value arguments for any of the previous input-argument combinations.

example

C2 = pidstd2 creates a controller object with default property values. To modify the property of the controller model, use dot notation.

example

C2 = pidstd2(sys) converts the dynamic system model sys to a standard-form pidstd2 controller object.

example

Input Arguments

expand all

`Kp` — Proportional gain
`1` (default) | scalar | vector | matrix | `realp` object | `genmat` object | `tunableSurface` object

Proportional gain, specified as a real and finite value or a tunable object.

To create a pidstd2 controller object, use a real and finite scalar value.
To create an array of pidstd2 controller objects, use an array of real and finite values.
To create a tunable controller model, use a tunable parameter (realp) or generalized matrix (genmat).
To create a tunable gain-scheduled controller model, use a tunable surface created using tunableSurface.

`Ti` — Integral time
`Inf` (default) | scalar | vector | matrix | `realp` object | `genmat` object | `tunableSurface` object

Integral time, specified as a real and positive value or a tunable object.

To create a pidstd2 controller object, use a real and positive scalar value.
To create an array of pidstd2 controller objects, use an array of real and positive values.
To create a tunable controller model, use a tunable parameter (realp) or generalized matrix (genmat).
To create a tunable gain-scheduled controller model, use a tunable surface created using tunableSurface.

`Td` — Derivative time
`0` (default) | scalar | vector | matrix | `realp` object | `genmat` object | `tunableSurface` object

Derivative time, specified as a real, finite, and nonnegative value or a tunable object.

To create a pidstd2 controller object, use a real, finite, and nonnegative scalar value.
To create an array of pidstd2 controller objects, use an array of real, finite, and nonnegative values.
To create a tunable controller model, use a tunable parameter (realp) or generalized matrix (genmat).
To create a tunable gain-scheduled controller model, use a tunable surface created using tunableSurface.

`N` — Derivative filter divisor
`Inf` (default) | scalar | vector | matrix | `realp` object | `genmat` object | `tunableSurface` object

First-order derivative filter divisor, specified as a real and positive value or a tunable object.

To create a pidstd2 controller object, use a real and positive scalar value.
To create an array of pidstd2 controller objects, use an array of real and positive values.
To create a tunable controller model, use a tunable parameter (realp) or generalized matrix (genmat).
To create a tunable gain-scheduled controller model, use a tunable surface created using tunableSurface.

When N = Inf, the controller has no filter on the derivative action.

`b` — Setpoint weighting on proportional term
`1` (default) | scalar | vector | matrix | `realp` object | `genmat` object | `tunableSurface` object

Setpoint weighting on the proportional term, specified as a real and finite value or a tunable object.

To create a pidstd2 controller object, use a real and finite scalar value.
To create an array of pidstd2 controller objects, use an array of real and finite values.
To create a tunable controller model, use a tunable parameter (realp) or generalized matrix (genmat).
To create a tunable gain-scheduled controller model, use a tunable surface created using tunableSurface.

When b = 0, changes in setpoint do not feed directly into the proportional term.

`c` — Setpoint weighting on derivative term
`1` (default) | scalar | vector | matrix | `realp` object | `genmat` object | `tunableSurface` object

Setpoint weighting on the derivative term, specified as a real and finite value or a tunable object.

To create a pidstd2 controller object, use a real and finite scalar value.
To create an array of pidstd2 controller objects, use an array of real and finite values.
To create a tunable controller model, use a tunable parameter (realp) or generalized matrix (genmat).
To create a tunable gain-scheduled controller model, use a tunable surface created using tunableSurface.

When c = 0, changes in setpoint do not feed directly into the derivative term.

`Ts` — Sample time
`0` (default) | positive scalar

Sample time, specified as:

0 for continuous-time systems.
A positive scalar representing the sampling period of a discrete-time system. Specify Ts in the time unit specified by the TimeUnit property.

In an array of pidstd2 controllers, the same Ts applies to all controllers.

PID controller models do not support unspecified sample time (Ts = -1).

Note

Changing Ts does not discretize or resample the model. To convert between continuous-time and discrete-time representations, use c2d and d2c. To change the sample time of a discrete-time system, use d2d.

The discrete integrator formulas of the discretized controller depend upon the c2d discretization method you use, as shown in this table.

`c2d` Discretization Method	`IFormula`	`DFormula`
`'zoh'`	`ForwardEuler`	`ForwardEuler`
`'foh'`	`Trapezoidal`	`Trapezoidal`
`'tustin'`	`Trapezoidal`	`Trapezoidal`
`'impulse'`	`ForwardEuler`	`ForwardEuler`
`'matched'`	`ForwardEuler`	`ForwardEuler`

For more information about c2d discretization methods, see c2d.

If you require different discrete integrator formulas, you can discretize the controller by directly setting Ts, IFormula, and DFormula to the desired values. However, this method does not compute new gain and filter-constant values for the discretized controller. Therefore, this method might yield a poorer match between the continuous-time and discrete-time PID controllers than using c2d.

`sys` — Dynamic system
dynamic system model | model array

Dynamic system, specified as a SISO dynamic system model or array of SISO dynamic system models. Dynamic systems that you can use include:

Continuous-time or discrete-time numeric LTI models, such as tf, zpk, ss, or pidstd models.
Generalized or uncertain LTI models such as genss or uss (Robust Control Toolbox) models.
The resulting PID controller assumes:
- Current values of the tunable components for tunable control design blocks.
- Nominal model values for uncertain control design blocks.
Identified LTI models, such as idtf (System Identification Toolbox), idss (System Identification Toolbox), idproc (System Identification Toolbox), idpoly (System Identification Toolbox), and idgrey (System Identification Toolbox) models.

Output Arguments

expand all

`C2` — 2-DOF standard-form PID controller model
`pidstd2` model object | `genss` model object

2-DOF PID controller, returned as:

A 2-DOF standard-form PID controller (pidstd2) model object, when all the gains have numeric values.
If one or more coefficients is a numeric array, C2 is an array of pidstd2 controller objects. The controller type (such as PI, PID, or PDF) depends upon the values of the gains. For example, when Td = 0, but Kp and Ti are nonzero and finite, C2 is a PI controller.
If one or more coefficients is a tunable parameter (realp), generalized matrix (genmat), or tunable gain surface (tunableSurface), then C2 is a generalized state-space model (genss).

Properties

expand all

`Kp, Ti, Td, N, b, c` — PID controller coefficients
scalars

PID controller coefficients, specified as scalars. When creating a pidstd2 controller object or array of objects, specify these coefficients in the Kp, Ti, Td, N, b, and c input arguments.

`IFormula` — Method for computing integral in discrete-time controller
`'ForwardEuler'` | `'BackwardEuler'` | `'Trapezoidal'`

Discrete integrator formula IF(z) for the integrator of the discrete-time pidstd2 controller:

$u = K_{p} [(b r - y) + \frac{1}{T_{i}} I F (z) (r - y) + \frac{T_{d}}{\frac{T_{d}}{N} + D F (z)} (c r - y)]$

Specify IFormula as one of the following:

'ForwardEuler' — IF(z) = $\frac{T_{s}}{z - 1} .$
This formula is best for small sample time, where the Nyquist limit is large compared to the bandwidth of the controller. For larger sample time, the ForwardEuler formula can result in instability, even when discretizing a system that is stable in continuous time.
'BackwardEuler' — IF(z) = $\frac{T_{s} z}{z - 1} .$
An advantage of the BackwardEuler formula is that discretizing a stable continuous-time system using this formula always yields a stable discrete-time result.
'Trapezoidal' — IF(z) = $\frac{T_{s}}{2} \frac{z + 1}{z - 1} .$
An advantage of the Trapezoidal formula is that discretizing a stable continuous-time system using this formula always yields a stable discrete-time result. Of all available integration formulas, the Trapezoidal formula yields the closest match between frequency-domain properties of the discretized system and the corresponding continuous-time system.

When C2 is a continuous-time controller, IFormula is ''.

`DFormula` — Method for computing derivative in discrete-time controller
`'ForwardEuler'` (default) | `'BackwardEuler'` | `'Trapezoidal'`

Discrete integrator formula DF(z) for the derivative filter of the discrete-time pidstd2 controller:

$u = K_{p} [(b r - y) + \frac{1}{T_{i}} I F (z) (r - y) + \frac{T_{d}}{\frac{T_{d}}{N} + D F (z)} (c r - y)]$

Specify DFormula as one of the following:

'ForwardEuler' — DF(z) = $\frac{T_{s}}{z - 1} .$
This formula is best for small sample time, where the Nyquist limit is large compared to the bandwidth of the controller. For larger sample time, the ForwardEuler formula can result in instability, even when discretizing a system that is stable in continuous time.
'BackwardEuler' — DF(z) = $\frac{T_{s} z}{z - 1} .$
An advantage of the BackwardEuler formula is that discretizing a stable continuous-time system using this formula always yields a stable discrete-time result.
'Trapezoidal' — DF(z) = $\frac{T_{s}}{2} \frac{z + 1}{z - 1} .$
An advantage of the Trapezoidal formula is that discretizing a stable continuous-time system using this formula always yields a stable discrete-time result. Of all available integration formulas, the Trapezoidal formula yields the closest match between frequency-domain properties of the discretized system and the corresponding continuous-time system.

The Trapezoidal value for DFormula is not available for a pidstd2 controller with no derivative filter (N = Inf).

When C2 is a continuous-time controller, DFormula is ''.

`InputDelay` — Input delay
0 (default)

This property is read-only.

Time delay on the system input. InputDelay is always 0 for a pidstd2 controller object.

`OutputDelay` — Output delay
0 (default)

This property is read-only.

Time delay on the system output. OutputDelay is always 0 for a pidstd2 controller object.

`Ts` — Sample time
`0` (default) | positive scalar

Sample time, specified as:

0 for continuous-time systems.
A positive scalar representing the sampling period of a discrete-time system. Ts in specified in the time unit specified by the TimeUnit property.

If pidstd2 is an array of PID controllers, the same Ts applies to all controllers.

`TimeUnit` — Time variable units
`'seconds'` (default) | `'nanoseconds'` | `'microseconds'` | `'milliseconds'` | `'minutes'` | `'hours'` | `'days'` | `'weeks'` | `'months'` | `'years'` | ...

Time variable units, specified as one of the following:

'nanoseconds'
'microseconds'
'milliseconds'
'seconds'
'minutes'
'hours'
'days'
'weeks'
'months'
'years'

Changing TimeUnit has no effect on other properties, but changes the overall system behavior. Use chgTimeUnit to convert between time units without modifying system behavior.

`InputName` — Input channel name
character vector | cell array of character vectors

Input channel name, specified as a character vector or a 2-by-1 cell array of character vectors. Use this property to name the input channels of the controller model. For example, assign the names setpoint and measurement to the inputs of a 2-DOF PID controller model C as follows.

C.InputName = {'setpoint';'measurement'};

Alternatively, use automatic vector expansion to assign both input names. For example:

C.InputName = 'C-input';

The input names automatically expand to {'C-input(1)';'C-input(2)'}.

You can use the shorthand notation u to refer to the InputName property. For example, C.u is equivalent to C.InputName.

Input channel names have several uses, including:

Identifying channels on model display and plots
Specifying connection points when interconnecting models

`InputUnit` — Input channel units
cell array of character vectors

Input channel units, specified as a 2-by-1 cell array of character vectors. Use this property to track input signal units. For example, assign the units Volts to the reference input and the concentration units mol/m^3 to the measurement input of a 2-DOF PID controller model C as follows.

C.InputUnit = {'Volts';'mol/m^3'};

InputUnit has no effect on system behavior.

`InputGroup` — Input channel groups
structure

Input channel groups. This property is not needed for PID controller models.

By default, InputGroup is a structure with no fields.

`OutputName` — Output channel names
`''` (default) | character vector

Output channel name, specified as one of the following:

A character vector.
'', no name specified.

For example, assign the name 'control' to the output of a controller model C as follows.

C.OutputName = 'control';

You can also use the shorthand notation y to refer to the OutputName property. For example, C.y is equivalent to C.OutputName.

Use OutputName to:

Identify channels on model display and plots.
Specify connection points when interconnecting models.

`OutputUnit` — Output channel units
`''` (default) | character vector

Output channel units, specified as one of the following:

A character vector.
'', no units specified.

Use OutputUnit to specify output signal units. OutputUnit has no effect on system behavior.

For example, assign the unit 'volts' to the output of a controller model C as follows.

C.OutputUnit = 'volts';

`OutputGroup` — Output channel groups
structure

Output channel groups. This property is not needed for PID controller models.

By default, OutputGroup is a structure with no fields.

`Notes` — User-specified text
`{}` (default) | character vector | cell array of character vectors

User-specified text that you want to associate with the system, specified as a character vector or cell array of character vectors. For example, 'System is MIMO'.

`UserData` — User-specified data
`[]` (default) | any MATLAB^® data type

User-specified data that you want to associate with the system, specified as any MATLAB data type.

`Name` — System name
`''` (default) | character vector

System name, specified as a character vector. For example, 'system_1'.

`SamplingGrid` — Sampling grid for model arrays
structure array

Sampling grid for model arrays, specified as a structure array.

Use SamplingGrid to track the variable values associated with each model in a model array, including identified linear time-invariant (IDLTI) model arrays.

Set the field names of the structure to the names of the sampling variables. Set the field values to the sampled variable values associated with each model in the array. All sampling variables must be numeric scalars, and all arrays of sampled values must match the dimensions of the model array.

For example, you can create an 11-by-1 array of linear models, sysarr, by taking snapshots of a linear time-varying system at times t = 0:10. The following code stores the time samples with the linear models.

 sysarr.SamplingGrid = struct('time',0:10)

Similarly, you can create a 6-by-9 model array, M, by independently sampling two variables, zeta and w. The following code maps the (zeta,w) values to M.

[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>)
M.SamplingGrid = struct('zeta',zeta,'w',w)

When you display M, each entry in the array includes the corresponding zeta and w values.

M(:,:,1,1) [zeta=0.3, w=5] =
 
        25
  --------------
  s^2 + 3 s + 25
 

M(:,:,2,1) [zeta=0.35, w=5] =
 
         25
  ----------------
  s^2 + 3.5 s + 25
 
...

For model arrays generated by linearizing a Simulink^® model at multiple parameter values or operating points, the software populates SamplingGrid automatically with the variable values that correspond to each entry in the array. For instance, the Simulink Control Design™ commands linearize (Simulink Control Design) and slLinearizer (Simulink Control Design) populate SamplingGrid automatically.

By default, SamplingGrid is a structure with no fields.

Object Functions

The following lists contain a representative subset of the functions you can use with pidstd2 models. In general, any function applicable to Dynamic System Models is applicable to a pidstd2 object.

expand all

Linear Analysis

`step`	Step response of dynamic system
`impulse`	Impulse response plot of dynamic system; impulse response data
`lsim`	Compute time response simulation data of dynamic system to arbitrary inputs
`bode`	Bode frequency response of dynamic system
`nyquist`	Nyquist response of dynamic system
`nichols`	Nichols response of dynamic system
`bandwidth`	Frequency response bandwidth

Stability Analysis

`pole`	Poles of dynamic system
`zero`	Zeros and gain of SISO dynamic system
`pzplot`	Plot pole-zero map of dynamic system
`margin`	Gain margin, phase margin, and crossover frequencies

Model Transformation

`zpk`	Zero-pole-gain model
`ss`	State-space model
`c2d`	Convert model from continuous to discrete time
`d2c`	Convert model from discrete to continuous time
`d2d`	Resample discrete-time model

Model Interconnection

`feedback`	Feedback connection of multiple models
`connect`	Block diagram interconnections of dynamic systems
`series`	Series connection of two models
`parallel`	Parallel connection of two models

Controller Design

`pidtune`	PID tuning algorithm for linear plant model
`rlocus`	Root locus of dynamic system
`piddata`	Access coefficients of parallel-form PID controller
`make2DOF`	Convert 1-DOF PID controller to 2-DOF controller
`pidTuner`	Open PID Tuner for PID tuning
`tunablePID`	Tunable PID controller

Examples

collapse all

2-DOF PDF Controller

Open Live Script

Create a continuous-time 2-DOF PDF controller in standard form. To do so, set the integral time constant to Inf. Set the other gains and the filter divisor to the desired values.

Kp = 1;
Ti = Inf;    % No integrator
Td = 3;      
N = 6;
b = 0.5;    % setpoint weight on proportional term
c = 0.5;    % setpoint weight on derivative term
C2 = pidstd2(Kp,Ti,Td,N,b,c)

C2 =
 
                              s      
  u = Kp * [(b*r-y) + Td * ------------ * (c*r-y)]
                          (Td/N)*s+1 

  with Kp = 1, Td = 3, N = 6, b = 0.5, c = 0.5
 
Continuous-time 2-DOF PDF controller in standard form

The display shows the controller type, formula, and parameter values, and verifies that the controller has no integrator term.

Discrete-Time 2-DOF PI Controller in Standard Form

Open Live Script

Create a discrete-time 2-DOF PI controller in standard form, using the trapezoidal discretization formula. Specify the formula using Name,Value syntax.

Kp = 1;
Ti = 2.4;
Td = 0;    
N = Inf; 
b = 0.5;   
c = 0;      
Ts = 0.1;
C2 = pidstd2(Kp,Ti,Td,N,b,c,Ts,'IFormula','Trapezoidal')

C2 =
 
                       1     Ts*(z+1)
  u = Kp * [(b*r-y) + ---- * -------- * (r-y)]
                       Ti    2*(z-1) 

  with Kp = 1, Ti = 2.4, b = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PI controller in standard form

Setting Td = 0 specifies a PI controller with no derivative term. As the display shows, the values of N and c are not used in this controller. The display also shows that the trapezoidal formula is used for the integrator.

2-DOF PID Controller with Named Inputs and Output

Open Live Script

Create a 2-DOF PID controller in standard form, and set the dynamic system properties InputName and OutputName. Naming the inputs and the output is useful, for example, when you interconnect the PID controller with other dynamic system models using the connect command.

C2 = pidstd2(1,2,3,10,1,1,'InputName',{'r','y'},'OutputName','u')

C2 =
 
                       1      1                      s      
  u = Kp * [(b*r-y) + ---- * --- * (r-y) + Td * ------------ * (c*r-y)]
                       Ti     s                  (Td/N)*s+1 

  with Kp = 1, Ti = 2, Td = 3, N = 10, b = 1, c = 1
 
Continuous-time 2-DOF PIDF controller in standard form

A 2-DOF PID controller has two inputs and one output. Therefore, the 'InputName' property is an array containing two names, one for each input. The model display does not show the input and output names for the PID controller, but you can examine the property values to see them. For instance, verify the input name of the controller.

C2.InputName

ans = 2x1 cell
    {'r'}
    {'y'}

Array of 2-DOF PID Controllers

Open Live Script

Create a 2-by-3 grid of 2-DOF PI controllers in standard form. The proportional gain ranges from 1–2 across the array rows, and the integrator time constant ranges from 5–9 across columns.

To build the array of PID controllers, start with arrays representing the gains.

Kp = [1 1 1;2 2 2];
Ti = [5:2:9;5:2:9];

When you pass these arrays to the pidstd2 command, the command returns the array of controllers.

pi_array = pidstd2(Kp,Ti,0,Inf,0.5,0,'Ts',0.1,'IFormula','BackwardEuler');
size(pi_array)

2x3 array of 2-DOF PID controller.
Each PID has 1 output and 2 inputs.

If you provide scalar values for some coefficients, pidstd2 automatically expands them and assigns the same value to all entries in the array. For instance, in this example, Td = 0, so that all entries in the array are PI controllers. Also, all entries in the array have b = 0.5.

Access entries in the array using array indexing. For dynamic system arrays, the first two dimensions are the I/O dimensions of the model, and the remaining dimensions are the array dimensions. Therefore, the following command extracts the (2,3) entry in the array.

pi23 = pi_array(:,:,2,3)

pi23 =
 
                       1      Ts*z 
  u = Kp * [(b*r-y) + ---- * ------ * (r-y)]
                       Ti      z-1 

  with Kp = 2, Ti = 9, b = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PI controller in standard form

You can also build an array of PID controllers using the stack command.

C2 = pidstd2(1,5,0.1,Inf,0.5,0.5);         % PID controller
C2f = pidstd2(1,5,0.1,0.5,0.5,0.5);        % PID controller with filter
pid_array = stack(2,C2,C2f);               % stack along 2nd array dimension

These commands return a 1-by-2 array of controllers.

size(pid_array)

1x2 array of 2-DOF PID controller.
Each PID has 1 output and 2 inputs.

All PID controllers in an array must have the same sample time, discrete integrator formulas, and dynamic system properties such as InputName and OutputName.

Convert 2-DOF PID Controller from Parallel to Standard Form

Open Live Script

Convert a parallel-form pid2 controller to standard form.

Parallel PID form expresses the controller actions in terms of proportional, integral, and derivative gains Kp, Ki, and Kd, and filter time constant Tf. You can convert a parallel-form pid2 controller to standard form using the pidstd2 command, provided that both of the following are true:

The pid2 controller can be expressed in valid standard form.
The gains Kp, Ki, and Kd of the pid2 controller all have the same sign.

For example, consider the following parallel-form controller.

Kp = 2;
Ki = 3;
Kd = 4;
Tf = 2;
b = 0.1;
c = 0.5;
C2_par = pid2(Kp,Ki,Kd,Tf,b,c)

C2_par =
 
                       1                s    
  u = Kp (b*r-y) + Ki --- (r-y) + Kd -------- (c*r-y)
                       s              Tf*s+1 

  with Kp = 2, Ki = 3, Kd = 4, Tf = 2, b = 0.1, c = 0.5
 
Continuous-time 2-DOF PIDF controller in parallel form.

Convert this controller to parallel form using pidstd2.

C2_std = pidstd2(C2_par)

C2_std =
 
                       1      1                      s      
  u = Kp * [(b*r-y) + ---- * --- * (r-y) + Td * ------------ * (c*r-y)]
                       Ti     s                  (Td/N)*s+1 

  with Kp = 2, Ti = 0.667, Td = 2, N = 1, b = 0.1, c = 0.5
 
Continuous-time 2-DOF PIDF controller in standard form

The display confirms the new standard form. A response plot confirms that the two forms are equivalent.

bodeplot(C2_par,'b-',C2_std,'r--')
legend('Parallel','Standard','Location','Southeast')

MATLAB figure

Convert Dynamic System to Standard-Form 2-DOF PID Controller

Open Live Script

Convert a two-input, one-output continuous-time dynamic system that represents a 2-DOF PID controller to a standard-form pidstd2 controller.

The following state-space matrices represent a 2-DOF PID controller.

A = [0,0;0,-8.181];
B = [1,-1;-0.1109,8.181];
C = [0.2301,10.66];
D = [0.8905,-11.79];
sys = ss(A,B,C,D);

Rewrite sys in terms of the standard-form PID parameters Kp, Ti, Td, and N, and the setpoint weights b and c.

C2 = pidstd2(sys)

C2 =
 
                       1      1                      s      
  u = Kp * [(b*r-y) + ---- * --- * (r-y) + Td * ------------ * (c*r-y)]
                       Ti     s                  (Td/N)*s+1 

  with Kp = 1.13, Ti = 4.91, Td = 1.15, N = 9.43, b = 0.66, c = 0.0136
 
Continuous-time 2-DOF PIDF controller in standard form

Convert Discrete-Time Dynamic System to 2-DOF Standard-Form PID Controller

Open Live Script

Convert a discrete-time dynamic system that represents a 2-DOF PID controller with derivative filter to standard pidstd2 form.

The following state-space matrices represent a discrete-time 2-DOF PID controller with a sample time of 0.05 s.

A = [1,0;0,0.6643];
B = [0.05,-0.05; -0.004553,0.3357];
C = [0.2301,10.66];
D = [0.8905,-11.79];
Ts = 0.05;
sys = ss(A,B,C,D,Ts);

When you convert sys to 2-DOF PID form, the result depends on which discrete integrator formulas you specify for the conversion. For instance, use the default, ForwardEuler, for both the integrator and the derivative.

C2fe = pidstd2(sys)

C2fe =
 
                       1       Ts                         1       
  u = Kp * [(b*r-y) + ---- * ------ * (r-y) + Td * --------------- * (c*r-y)]
                       Ti      z-1                 (Td/N)+Ts/(z-1)

  with Kp = 1.13, Ti = 4.91, Td = 1.41, N = 9.43, b = 0.66, c = 0.0136, Ts = 0.05
 
Sample time: 0.05 seconds
Discrete-time 2-DOF PIDF controller in standard form

Now convert using the Trapezoidal formula.

C2trap = pidstd2(sys,'IFormula','Trapezoidal','DFormula','Trapezoidal')

C2trap =
 
                       1     Ts*(z+1)                           1           
  u = Kp * [(b*r-y) + ---- * -------- * (r-y) + Td * ----------------------- * (c*r-y)]
                       Ti    2*(z-1)                 (Td/N)+Ts/2*(z+1)/(z-1)

  with Kp = 1.12, Ti = 4.89, Td = 1.41, N = 11.4, b = 0.658, c = 0.0136, Ts = 0.05
 
Sample time: 0.05 seconds
Discrete-time 2-DOF PIDF controller in standard form

The displays show the difference in resulting coefficient values and functional form.

For some dynamic systems, attempting to use the Trapezoidal or BackwardEuler integrator formulas yields invalid results, such as negative Ti, Td, or N values. In such cases, pidstd2 returns an error.

Discretize a Standard-Form 2-DOF PID Controller

Open Live Script

Discretize a continuous-time standard-form 2-DOF PID controller and specify the integral and derivative filter formulas.

Create a continuous-time pidstd2 controller and discretize it using the zero-order-hold method of the c2d command.

C2con = pidstd2(10,5,3,0.5,1,1);  % continuous-time 2-DOF PIDF controller
C2dis1 = c2d(C2con,0.1,'zoh')

C2dis1 =
 
                       1       Ts                         1       
  u = Kp * [(b*r-y) + ---- * ------ * (r-y) + Td * --------------- * (c*r-y)]
                       Ti      z-1                 (Td/N)+Ts/(z-1)

  with Kp = 10, Ti = 5, Td = 3.03, N = 0.5, b = 1, c = 1, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in standard form

The display shows that c2d computes new PID coefficients for the discrete-time controller.

The discrete integrator formulas of the discretized controller depend on the c2d discretization method, as described in Tips. For the zoh method, both IFormula and DFormula are ForwardEuler.

C2dis1.IFormula

ans = 
'ForwardEuler'

C2dis1.DFormula

ans = 
'ForwardEuler'

If you want to use different formulas from the ones returned by c2d, then you can directly set the Ts, IFormula, and DFormula properties of the controller to the desired values.

C2dis2 = C2con;
C2dis2.Ts = 0.1; 
C2dis2.IFormula = 'BackwardEuler';
C2dis2.DFormula = 'BackwardEuler';

However, these commands do not compute new coefficients for the discretized controller. To see this, examine C2dis2 and compare the coefficients to C2con and C2dis1.

C2dis2

C2dis2 =
 
                       1      Ts*z                         1        
  u = Kp * [(b*r-y) + ---- * ------ * (r-y) + Td * ----------------- * (c*r-y)]
                       Ti      z-1                 (Td/N)+Ts*z/(z-1)

  with Kp = 10, Ti = 5, Td = 3, N = 0.5, b = 1, c = 1, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in standard form

Tips

To break a 2-DOF controller into two SISO control components, such as a feedback controller and a feedforward controller, use getComponents.
Create arrays of pidstd2 controllers by:
- Specifying array values for one or more of the coefficients Kp, Ti, Td, N, b, and c.
- Specifying an array of dynamic systems sys to convert to pid2 controller objects.
- Using stack to build arrays from individual controllers or smaller arrays.
- Passing an array of plant models to pidtune.
In an array of pidstd2 controllers, each controller must have the same sample time Ts and discrete integrator formulas IFormula and DFormula.
To create or convert to a parallel-form controller, use pid2. Parallel form expresses the controller actions in terms of proportional, integral, and derivative gains K_p, K_i and K_d, and a filter time constant T_f. For example, the relationship between the inputs and output of a continuous-time parallel-form 2-DOF PID controller is given by:
$u = K_{p} (b r - y) + \frac{K_{i}}{s} (r - y) + \frac{K_{d} s}{T_{f} s + 1} (c r - y)$
There are two ways to discretize a continuous-time pidstd2 controller:
- Use the c2d command. c2d computes new parameter values for the discretized controller. The discrete integrator formulas of the discretized controller depend upon the c2d discretization method you use, as shown in the following table.
  c2d Discretization Method IFormula DFormula
  'zoh' ForwardEuler ForwardEuler
  'foh' Trapezoidal Trapezoidal
  'tustin' Trapezoidal Trapezoidal
  'impulse' ForwardEuler ForwardEuler
  'matched' ForwardEuler ForwardEuler
  For more information about c2d discretization methods, See the c2d reference page. For more information about IFormula and DFormula, see Properties.
- If you require different discrete integrator formulas, you can discretize the controller by directly setting Ts, IFormula, and DFormula to the desired values. (See Discretize a Standard-Form 2-DOF PID Controller.) However, this method does not compute new gain and filter-constant values for the discretized controller. Therefore, this method might yield a poorer match between the continuous- and discrete-time pidstd2 controllers than using c2d.

Version History

Introduced in R2015b

pidstd2

Description

Creation

Syntax

Description

Input Arguments

Kp — Proportional gain 1 (default) | scalar | vector | matrix | realp object | genmat object | tunableSurface object

Ti — Integral time Inf (default) | scalar | vector | matrix | realp object | genmat object | tunableSurface object

Td — Derivative time 0 (default) | scalar | vector | matrix | realp object | genmat object | tunableSurface object

N — Derivative filter divisor Inf (default) | scalar | vector | matrix | realp object | genmat object | tunableSurface object

b — Setpoint weighting on proportional term 1 (default) | scalar | vector | matrix | realp object | genmat object | tunableSurface object

c — Setpoint weighting on derivative term 1 (default) | scalar | vector | matrix | realp object | genmat object | tunableSurface object

Ts — Sample time 0 (default) | positive scalar

sys — Dynamic system dynamic system model | model array

Output Arguments

C2 — 2-DOF standard-form PID controller model pidstd2 model object | genss model object

Properties

Kp, Ti, Td, N, b, c — PID controller coefficients scalars

IFormula — Method for computing integral in discrete-time controller 'ForwardEuler' | 'BackwardEuler' | 'Trapezoidal'

DFormula — Method for computing derivative in discrete-time controller 'ForwardEuler' (default) | 'BackwardEuler' | 'Trapezoidal'

InputDelay — Input delay 0 (default)

OutputDelay — Output delay 0 (default)

Ts — Sample time 0 (default) | positive scalar

TimeUnit — Time variable units 'seconds' (default) | 'nanoseconds' | 'microseconds' | 'milliseconds' | 'minutes' | 'hours' | 'days' | 'weeks' | 'months' | 'years' | ...

InputName — Input channel name character vector | cell array of character vectors

InputUnit — Input channel units cell array of character vectors

InputGroup — Input channel groups structure

OutputName — Output channel names '' (default) | character vector

OutputUnit — Output channel units '' (default) | character vector

OutputGroup — Output channel groups structure

Notes — User-specified text {} (default) | character vector | cell array of character vectors

UserData — User-specified data [] (default) | any MATLAB® data type

Name — System name '' (default) | character vector

SamplingGrid — Sampling grid for model arrays structure array

Object Functions

Linear Analysis

Stability Analysis

Model Transformation

Model Interconnection

Controller Design

Examples

2-DOF PDF Controller

Discrete-Time 2-DOF PI Controller in Standard Form

2-DOF PID Controller with Named Inputs and Output

Array of 2-DOF PID Controllers

Convert 2-DOF PID Controller from Parallel to Standard Form

Convert Dynamic System to Standard-Form 2-DOF PID Controller

Convert Discrete-Time Dynamic System to 2-DOF Standard-Form PID Controller

Discretize a Standard-Form 2-DOF PID Controller

Tips

Version History

See Also

Topics

`Kp` — Proportional gain
`1` (default) | scalar | vector | matrix | `realp` object | `genmat` object | `tunableSurface` object

`Ti` — Integral time
`Inf` (default) | scalar | vector | matrix | `realp` object | `genmat` object | `tunableSurface` object

`Td` — Derivative time
`0` (default) | scalar | vector | matrix | `realp` object | `genmat` object | `tunableSurface` object

`N` — Derivative filter divisor
`Inf` (default) | scalar | vector | matrix | `realp` object | `genmat` object | `tunableSurface` object

`b` — Setpoint weighting on proportional term
`1` (default) | scalar | vector | matrix | `realp` object | `genmat` object | `tunableSurface` object

`c` — Setpoint weighting on derivative term
`1` (default) | scalar | vector | matrix | `realp` object | `genmat` object | `tunableSurface` object

`Ts` — Sample time
`0` (default) | positive scalar

`sys` — Dynamic system
dynamic system model | model array

`C2` — 2-DOF standard-form PID controller model
`pidstd2` model object | `genss` model object

`Kp, Ti, Td, N, b, c` — PID controller coefficients
scalars

`IFormula` — Method for computing integral in discrete-time controller
`'ForwardEuler'` | `'BackwardEuler'` | `'Trapezoidal'`

`DFormula` — Method for computing derivative in discrete-time controller
`'ForwardEuler'` (default) | `'BackwardEuler'` | `'Trapezoidal'`

`InputDelay` — Input delay
0 (default)

`OutputDelay` — Output delay
0 (default)

`Ts` — Sample time
`0` (default) | positive scalar

`TimeUnit` — Time variable units
`'seconds'` (default) | `'nanoseconds'` | `'microseconds'` | `'milliseconds'` | `'minutes'` | `'hours'` | `'days'` | `'weeks'` | `'months'` | `'years'` | ...

`InputName` — Input channel name
character vector | cell array of character vectors

`InputUnit` — Input channel units
cell array of character vectors

`InputGroup` — Input channel groups
structure

`OutputName` — Output channel names
`''` (default) | character vector

`OutputUnit` — Output channel units
`''` (default) | character vector

`OutputGroup` — Output channel groups
structure

`Notes` — User-specified text
`{}` (default) | character vector | cell array of character vectors

`UserData` — User-specified data
`[]` (default) | any MATLAB^® data type

`Name` — System name
`''` (default) | character vector

`SamplingGrid` — Sampling grid for model arrays
structure array