Trim and Linearize an Airframe
This example shows how to trim and linearize an airframe using Simulink® Control Design™ software.
The goal is to find the elevator deflection and the resulting trimmed body rate that generate a given angle of incidence when the airframe is traveling at a set speed.
Once you find the trim condition, you can compute a linear model for the dynamics of the states around the trim condition.
Fixed parameters:
Angle of incidence (
Theta)Body attitude (
U)Position
Trimmed steady-state parameters:
Elevator deflection (
w)Body rate (
q)
Compute Operating Points
Open the model.
mdl = 'scdairframe';
open_system(mdl)
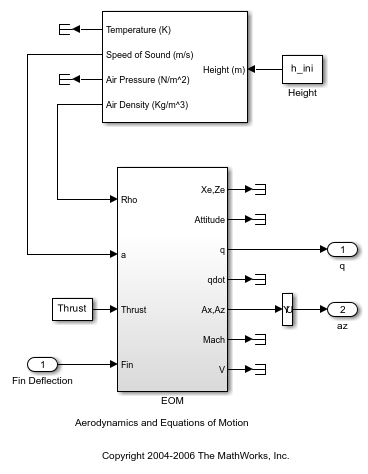
Create an operating point specification object for the model using the model initial conditions.
opspec = operspec(mdl)
opspec =
Operating point specification for the Model scdairframe.
(Time-Varying Components Evaluated at time t=0)
States:
----------
x Known SteadyState Min Max dxMin dxMax
___________ ___________ ___________ ___________ ___________ ___________ ___________
(1.) scdairframe/EOM/ Equations of Motion (Body Axes)/Position
0 false true -Inf Inf -Inf Inf
-3047.9999 false true -Inf Inf -Inf Inf
(2.) scdairframe/EOM/ Equations of Motion (Body Axes)/Theta
0 false true -Inf Inf -Inf Inf
(3.) scdairframe/EOM/ Equations of Motion (Body Axes)/U,w
984 false true -Inf Inf -Inf Inf
0 false true -Inf Inf -Inf Inf
(4.) scdairframe/EOM/ Equations of Motion (Body Axes)/q
0 false true -Inf Inf -Inf Inf
Inputs:
----------
u Known Min Max
_____ _____ _____ _____
(1.) scdairframe/Fin Deflection
0 false -Inf Inf
Outputs:
----------
y Known Min Max
_____ _____ _____ _____
(1.) scdairframe/q
0 false -Inf Inf
(2.) scdairframe/az
0 false -Inf Inf
Specify which states in the model are:
Known at the operating point
At steady state at the operating point
Specify that the Position states are known and not at steady state. For the state values, specified in opspec.States(1).x, use the default values from the model initial condition.
opspec.States(1).Known = [1;1]; opspec.States(1).SteadyState = [0;0];
Specify that the second state, which corresponds to the angle of incidence Theta, is known but not at steady state. As with the position states, use the default state value from the model initial condition.
opspec.States(2).Known = 1; opspec.States(2).SteadyState = 0;
The third state specification includes the body axis angular rates U and w. Specify that both states are known at the operating point and that w is at steady state.
opspec.States(3).Known = [1 1]; opspec.States(3).SteadyState = [0 1];
Search for the operating point that meets these specifications.
op = findop(mdl,opspec);
Operating point search report:
---------------------------------
opreport =
Operating point search report for the Model scdairframe.
(Time-Varying Components Evaluated at time t=0)
Operating point specifications were successfully met.
States:
----------
Min x Max dxMin dx dxMax
___________ ___________ ___________ ___________ ___________ ___________
(1.) scdairframe/EOM/ Equations of Motion (Body Axes)/Position
0 0 0 -Inf 984 Inf
-3047.9999 -3047.9999 -3047.9999 -Inf 0 Inf
(2.) scdairframe/EOM/ Equations of Motion (Body Axes)/Theta
0 0 0 -Inf -0.0097235 Inf
(3.) scdairframe/EOM/ Equations of Motion (Body Axes)/U,w
984 984 984 -Inf 22.6897 Inf
0 0 0 0 -1.4367e-11 0
(4.) scdairframe/EOM/ Equations of Motion (Body Axes)/q
-Inf -0.0097235 Inf 0 1.1477e-16 0
Inputs:
----------
Min u Max
_________ _________ _________
(1.) scdairframe/Fin Deflection
-Inf 0.0014161 Inf
Outputs:
----------
Min y Max
__________ __________ __________
(1.) scdairframe/q
-Inf -0.0097235 Inf
(2.) scdairframe/az
-Inf -0.24207 Inf
Linearize Model
To linearize the model at the computed operating point, first specify the linearization input and output points.
io(1) = linio('scdairframe/Fin Deflection',1,'input'); io(2) = linio('scdairframe/EOM',3,'output'); io(3) = linio('scdairframe/Selector',1,'output');
Linearize the model at the operating point.
sys = linearize(mdl,op,io);
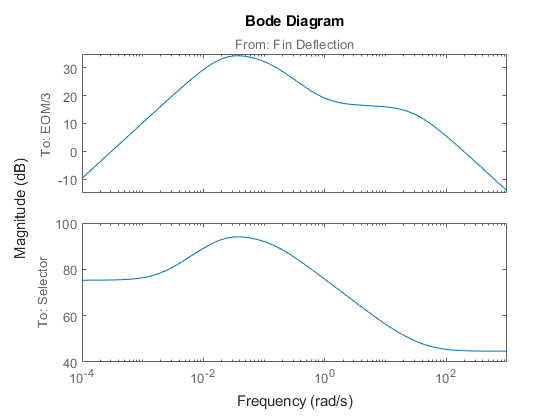
Plot the Bode magnitude response for the linear model.
bodemag(sys)
bdclose('scdairframe')
See Also
operspec | findop | linio | linearize