PI Section Line
(To be removed) Implement transmission line or cable with lumped parameters
The Specialized Power Systems library will be removed in R2026a. Use the Simscape™ Electrical™ blocks and functions instead. For more information on updating your models, see Upgrade Specialized Power System Models to use Simscape Electrical Blocks.
Libraries:
Simscape /
Electrical /
Specialized Power Systems /
Power Grid Elements
Description
The PI Section Line block implements an N-phase transmission line or cable with parameters lumped in PI sections.
For a transmission line, the resistance, inductance, and capacitance are uniformly distributed along the line. An approximate model of the distributed parameter line is obtained by cascading several identical PI sections. The following figure shows one PI section of a three-phase transmission line.
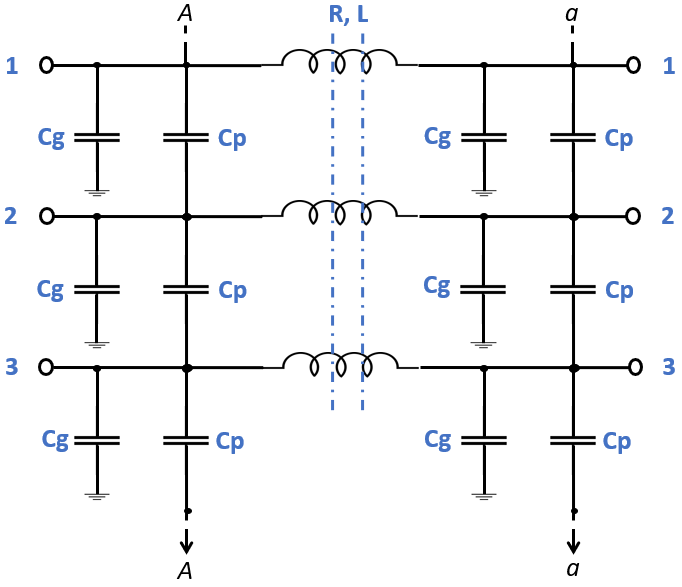
When the number of phases is greater than 1, the series resistance and inductance are implemented by a mutual inductance device defined by the R and L matrices.
When the number of phases is 1, the series resistance and inductance are modeled by a single resistance R and inductance L. The phase-to-phase capacitors, Cp, are not modeled.
The shunt capacitance Cg of each phase and the phase-to-phase capacitance Cp are defined as:
| Cg = sum(C(:,p)) / 2; | (1) |
| Cp = -C(p,k) | (2) |
where C is the capacitance matrix and p and k are the number of the phases to which Cp is connected.
Unlike the Distributed Parameters Line block, which has an infinite number of states, the PI section linear model has a finite number of states that permit you to compute a linear state-space model. The number of sections to be used depends on the frequency range to be represented.
An approximation of the maximum frequency range represented by the PI line model is given by the following equation:
where
| Nbpi | Number of PI sections |
| v | Propagation speed (km/s) = ; l in H/km, c in F/km |
| ltot | Line length (km) |
For example, for a 100 km aerial line having a propagation speed of 300,000 km/s, the maximum frequency range represented with a single PI section is approximately 375 Hz. For studying interactions between a power system and a control system, this simple model could be sufficient. However for switching surge studies involving high-frequency transients in the kHz range, much shorter PI sections should be used. In fact, you can obtain the most accurate results by using a distributed parameters line model.
Note
The powergui block provides the Power Line Parameters app and the Power Cable Parameters app, which calculates resistance, inductance, and capacitance per unit of length based on the line or cable geometry and the conductor characteristics.
Hyperbolic Correction of RLC Elements
For short line sections (approximately lsec <50 km) the RLC elements for each line section are simply given by:
where
| r | Resistance per unit length (Ω/km) |
| l | Inductance per unit length (H/km) |
| c | Capacitance per unit length (F/km) |
| f | Frequency (Hz) |
| lsec | Line section length = ltot / N (km) |
However, for long line sections, the RLC elements given by the above equations must be corrected in order to get an exact line model at a specified frequency. The RLC elements are then computed using hyperbolic functions as explained below.
Per unit length series impedance at frequency f is
Per unit length shunt admittance at frequency f is
Characteristic impedance is
Propagation constant is
Hyperbolic corrections result in RLC values slightly different from the non-corrected values. R and L are decreased while C is increased. These corrections become more important as line section length is increasing. For example, let us consider a 735 kV line with the following positive-sequence and zero-sequence parameters (these are the default parameters of the Three-Phase PI Section Line block and Distributed Parameters Line block):
Positive sequence |
| |||
Zero sequence |
|
For a 350 km line section, noncorrected RLC positive-sequence values are:
Hyperbolic correction at 60 Hz yields:
For these particular parameters and long line section (350 km), corrections for positive-sequence RLC elements are relatively important (respectively −6.8%, −3.4%, and + 1.8%). For zero-sequence parameters, you can verify that even higher RLC corrections must be applied (respectively −18%, −8.5%, and +4.9%).
The PI Section Line block always uses the hyperbolic correction, regardless of the line section length.
Parameters
Extended Capabilities
Version History
Introduced before R2006a