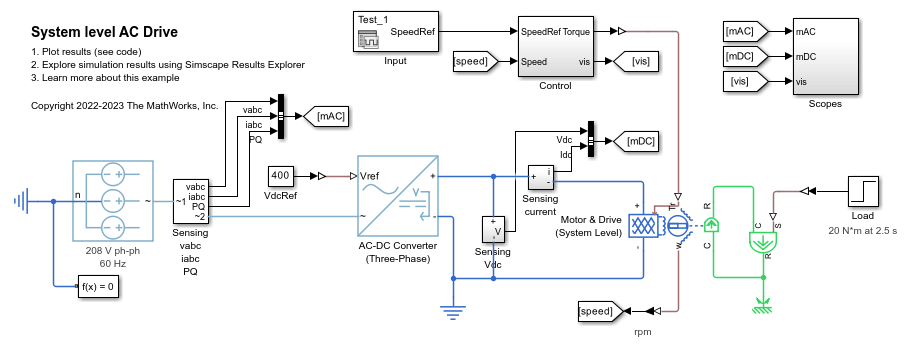
AC-DC Converter (Three-Phase)

Behavioral model of AC-DC converter

Since R2022b

Libraries:
Simscape / Electrical / Semiconductors & Converters / Converters

Description

This block represents the behavioral model of an AC-DC converter. Use this block to model AC-DC converters without simulating individual switching events. Use the DC voltage reference input to convert the electrical energy between the AC and DC sides.

This block is compatible with time simulation mode and frequency-and-time simulation mode.

Equations

DC Side

At the DC side, if you set the Voltage dynamics at DC side parameter to No dynamics, the block calculates the output voltage, V_DC, by using this equation:

$V_{DC} = V_{ref} - D I_{DC},$

where V_ref is the value of the input signal at the Vref port, D is the value of the Output DC voltage droop with output current parameter, and I_DC is the output DC current.

If you set the Voltage dynamics at DC side parameter to Specify voltage regulation time constant, the block calculates the output voltage, V_DC, by using this equation:

$τ_{DC} {\dot{V}}_{DC} + V_{DC} = V_{ref} - D I_{DC},$

where τ_DC is the value of the Voltage regulation time constant at DC side parameter.

The power at the DC side is

$P_{DC} = V_{DC} I_{DC} .$

AC Side

If you set the Power balance dynamics parameter to No dynamics, the input power at the AC side is equal to the output power at the DC side.

$P_{AC} = P_{DC} .$

If you set the Power balance dynamics parameter to Specify power time constant, the block calculates the input power at the AC side by using this equation:

$τ_{P} {\dot{P}}_{AC} + P_{AC} = P_{DC},$

where τ_P is the value of the Power balance time constant parameter.

To determine the three-phase input currents at the AC side, the block first calculates the dq-axes voltages, v_d and v_q, using the Park transform on the abc-phase voltages, v_a, v_b, and v_c:

$[\begin{matrix} v_{d} \\ v_{q} \end{matrix}] = \frac{2}{3} [\begin{matrix} \sin θ & \sin (θ - 120 °) & \sin (θ + 120 °) \\ \cos θ & \cos (θ - 120 °) & \cos (θ + 120 °) \end{matrix}] [\begin{matrix} v_{a} \\ v_{b} \\ v_{c} \end{matrix}]$

where $θ = 2 π F_{rated} \cdot t$ is the angle of the synchronously rotating reference frame.

The block then calculates the three-phase AC currents, i_a, i_b, and i_c, by using these power equations:

$\begin{array}{l} P_{AC} = \frac{3}{2} (v_{d} i_{d} + v_{q} i_{q}) \\ Q_{AC} = 0 = \frac{3}{2} (v_{d} i_{d} - v_{q} i_{q}) . \end{array}$

From these equations, the dq-axes currents, i_d and i_q, are

$\begin{array}{l} i_{d} = \frac{2}{3} \frac{P_{AC} v_{dx}}{v_{dx}^{2} + v_{qx}^{2}} \\ i_{q} = \frac{2}{3} \frac{P_{AC} v_{qx}}{v_{dx}^{2} + v_{qx}^{2}}, \end{array}$

where v_dx and v_qx are obtained from these equations:

$\begin{array}{l} τ_{AC} {\dot{v}}_{dx} + v_{dx} = v_{d} \\ τ_{AC} {\dot{v}}_{qx} + v_{qx} = v_{q}, \end{array}$

where τ_AC is the value of the Voltage time constant at AC side parameter.

Finally, the block calculates the three-phase AC currents that flow into the converter by using this equation:

$[\begin{matrix} i_{a} \\ i_{b} \\ i_{c} \end{matrix}] = [\begin{matrix} \sin θ & \cos θ \\ \sin (θ - 120 °) & \cos (θ - 120 °) \\ \sin (θ + 120 °) & \cos (θ + 120 °) \end{matrix}] [\begin{matrix} i_{d} \\ i_{q} \end{matrix}] .$

Examples

System-Level AC Drive

Model a system-level AC drive for an electric machine by using the AC-DC Converter (Three-Phase) block and Motor & Drive (System Level) block. The AC-DC converter represents a grid-side converter which provides a constant DC-link voltage. The Motor & Drive block acts as a generic AC electric machine with its DC-AC converter. This modeling approach provides fast system-level simulation without the switching events of the power converters.

Open Model

Limitations

The AC-DC Converter (Three-Phase) block does not model the power losses.

Ports

Input

expand all

Vref — DC voltage reference
physical

Physical signal input port associated with the external signal of the DC voltage reference.

Conserving

expand all

~ — Three-phase port
electrical

Expandable three-phase port.

Dependencies

To enable this port, set Electrical connection to Composite three-phase ports.

a — a-phase
electrical

Electrical conserving port associated with the a-phase.

Dependencies

To enable this port, set Electrical connection to Expanded three-phase ports.

b — b-phase
electrical

Electrical conserving port associated with the b-phase.

Dependencies

To enable this port, set Electrical connection to Expanded three-phase ports.

c — c-phase
electrical

Electrical conserving port associated with the c-phase.

Dependencies

To enable this port, set Electrical connection to Expanded three-phase ports.

+ — Positive terminal
electrical

Electrical conserving port associated with the positive terminal.

- — Negative terminal
electrical

Electrical conserving port associated with the negative terminal.

Parameters

expand all

Electrical connection — Electrical connection
`Composite three-phase ports` (default) | `Expanded three-phase ports`

Option to model composite or expanded three-phase ports.

Output DC voltage droop with output current — Voltage droop at 1 A
`1V/A` (default) | nonnegative scalar

Amount of voltage that the output DC voltage drops from the set point for an output current of 1 A.

Voltage dynamics at DC side — Dynamics model at DC side
`No dynamics` (default) | `Specify voltage regulation time constant`

Option to include voltage regulation dynamics. If you set this parameter to No dynamics, the block does not consider the voltage regulation dynamics. If you set this parameter to Specify voltage regulation time constant, the block adds a first-order lag to the equation that defines the value of the DC voltage source.

Voltage regulation time constant at DC side — Voltage dynamics time constant at DC side
`0.02` `s` (default) | positive scalar

Time constant associated with the voltage transients at the DC side when the load current at the DC side is stepped.

Dependencies

To enable this parameter, set Voltage dynamics at DC side to Specify voltage regulation time constant.

Initial output voltage at DC side — Output voltage at DC side at time zero
`100` `V` (default) | scalar

DC side output voltage at time zero. To initialize the model with no transients when it delivers a steady-state load current, use this parameter to set the initial DC side output voltage.

Dependencies

To enable this parameter, set Voltage dynamics at DC side to Specify voltage regulation time constant.

Rated electrical frequency at AC side — Rated electrical frequency at AC side
`60` `Hz` (default) | positive scalar

Rated electrical frequency at AC side.

Minimum AC side voltage (phase-to-phase RMS) — Minimum AC-side voltage
`80` `V` (default) | positive scalar

Minimum value of the phase-to-phase RMS AC-side voltage for the converter to produce a DC output voltage.

Voltage time constant at AC side — Voltage time constant at AC-side
`0.01` `s` (default) | positive scalar

Time constant associated with the voltage measurement transients at the AC side.

Initial voltage at AC side (phase-to-phase RMS) — AC-side initial voltage
`100` `V` (default) | positive scalar

Phase-to-phase RMS voltage at the AC-side at time zero. The value of this parameter must be greater than the value of the Minimum AC side voltage (phase-to-phase RMS) parameter.

Initial voltage angle at AC side — Initial voltage angle of a-phase at AC side
`0` `deg` (default) | scalar

Initial voltage angle of the a-phase at time zero for the AC side.

Power balance dynamics — Option to include power balance dynamics
`Specify power time constant` (default) | `No dynamics`

Whether to include power balance dynamics. If you set this parameter to No dynamics, the block does not consider power balance dynamics. If you set this parameter to Specify power time constant, the block adds a first-order lag to the equation that defines the AC-side power. When you enable the dynamics, a DC-side output power change results in a transient change in the input power at the AC side.

Power balance time constant — Time constant for power balance dynamics
`0.01` `s` (default) | positive scalar

Time constant associated with the transients of the power balance between the AC and DC side.

Dependencies

To enable this parameter, set Power balance dynamics to Specify power time constant.

Initial active power — Initial active power at AC side
`1e3` `W` (default) | scalar

Initial active power at time zero at the AC side.

Dependencies

To enable this parameter, set Power balance dynamics to Specify power time constant.

AC-DC Converter (Three-Phase)

Description

Equations

Examples

System-Level AC Drive

Limitations

Ports

Input

Vref — DC voltage reference physical

Conserving

~ — Three-phase port electrical

Dependencies

a — a-phase electrical

Dependencies

b — b-phase electrical

Dependencies

c — c-phase electrical

Dependencies

+ — Positive terminal electrical

- — Negative terminal electrical

Parameters

Electrical connection — Electrical connection Composite three-phase ports (default) | Expanded three-phase ports

Output DC voltage droop with output current — Voltage droop at 1 A 1V/A (default) | nonnegative scalar

Voltage dynamics at DC side — Dynamics model at DC side No dynamics (default) | Specify voltage regulation time constant

Voltage regulation time constant at DC side — Voltage dynamics time constant at DC side 0.02 s (default) | positive scalar

Dependencies

Initial output voltage at DC side — Output voltage at DC side at time zero 100 V (default) | scalar

Dependencies

Rated electrical frequency at AC side — Rated electrical frequency at AC side 60 Hz (default) | positive scalar

Minimum AC side voltage (phase-to-phase RMS) — Minimum AC-side voltage 80 V (default) | positive scalar

Voltage time constant at AC side — Voltage time constant at AC-side 0.01 s (default) | positive scalar

Initial voltage at AC side (phase-to-phase RMS) — AC-side initial voltage 100 V (default) | positive scalar

Initial voltage angle at AC side — Initial voltage angle of a-phase at AC side 0 deg (default) | scalar

Power balance dynamics — Option to include power balance dynamics Specify power time constant (default) | No dynamics

Power balance time constant — Time constant for power balance dynamics 0.01 s (default) | positive scalar

Dependencies

Initial active power — Initial active power at AC side 1e3 W (default) | scalar

Dependencies

Parasitic conductance to electrical reference — Parasitic conductance to electrical reference 1e-6 S (default) | nonnegative scalar

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

See Also

Vref — DC voltage reference
physical

~ — Three-phase port
electrical

a — a-phase
electrical

b — b-phase
electrical

c — c-phase
electrical

+ — Positive terminal
electrical

- — Negative terminal
electrical

Electrical connection — Electrical connection
`Composite three-phase ports` (default) | `Expanded three-phase ports`

Output DC voltage droop with output current — Voltage droop at 1 A
`1V/A` (default) | nonnegative scalar

Voltage dynamics at DC side — Dynamics model at DC side
`No dynamics` (default) | `Specify voltage regulation time constant`

Voltage regulation time constant at DC side — Voltage dynamics time constant at DC side
`0.02` `s` (default) | positive scalar

Initial output voltage at DC side — Output voltage at DC side at time zero
`100` `V` (default) | scalar

Rated electrical frequency at AC side — Rated electrical frequency at AC side
`60` `Hz` (default) | positive scalar

Minimum AC side voltage (phase-to-phase RMS) — Minimum AC-side voltage
`80` `V` (default) | positive scalar

Voltage time constant at AC side — Voltage time constant at AC-side
`0.01` `s` (default) | positive scalar

Initial voltage at AC side (phase-to-phase RMS) — AC-side initial voltage
`100` `V` (default) | positive scalar

Initial voltage angle at AC side — Initial voltage angle of a-phase at AC side
`0` `deg` (default) | scalar

Power balance dynamics — Option to include power balance dynamics
`Specify power time constant` (default) | `No dynamics`

Power balance time constant — Time constant for power balance dynamics
`0.01` `s` (default) | positive scalar

Initial active power — Initial active power at AC side
`1e3` `W` (default) | scalar

Parasitic conductance to electrical reference — Parasitic conductance to electrical reference
`1e-6` `S` (default) | nonnegative scalar

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.