PMSM (Four-Phase)
Four-phase permanent magnet synchronous motor with sinusoidal flux distribution
Since R2022a
Libraries:
Simscape /
Electrical /
Electromechanical /
Permanent Magnet
Description
The PMSM (Four-Phase) block models a permanent magnet synchronous motor (PMSM) with a four-phase cross-wound or square-wound stator. Use this block to model these types of motor if the motor has four stator windings: interior permanent magnet synchronous machine (IPMSM), surface permanent magnet synchronous machine (SPMSM), axial flux (pancake) motor, or PMSM servomotor. The figure shows the equivalent electrical circuits for the cross-connected and square-connected stator windings.
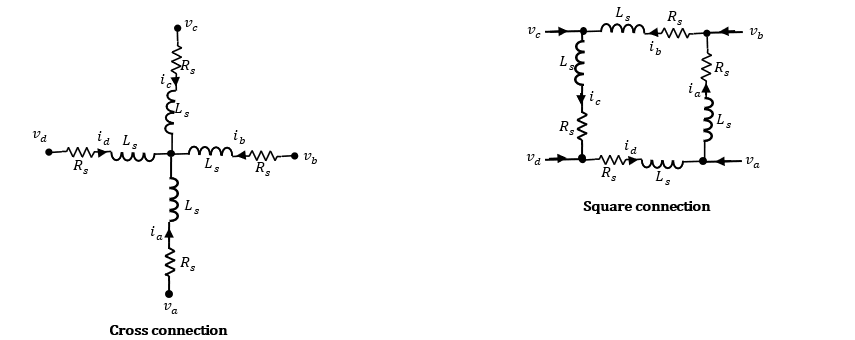
Motor Construction
Permanent magnets generate a rotor magnetic field that creates a sinusoidal rate of change of flux based on the rotor angle.
For the axes convention, when you set the Rotor angle
definition parameter to Angle between the a-phase
magnetic axis and the d-axis, the a-phase and
permanent magnet fluxes align when the rotor mechanical angle,
θr, is zero. When you set the
Rotor angle definition parameter to Angle
between the a-phase magnetic axis and the q-axis, the rotor
mechanical angle is the angle between the a-phase magnetic axis
and the rotor q-axis.
Equations
The voltages across the stator windings are
where:
va, vb, vc, and vd are the individual phase voltages across the stator windings.
Rs is the equivalent resistance of each stator winding.
ia, ib, ic, and id are the currents flowing in the stator windings.
and are the rates of change for the magnetic flux in each stator winding.
The permanent magnet and the four windings contribute to the total flux linking each winding. The total flux is
where:
ψa, ψb, ψc, and ψd are the total fluxes that link each stator winding.
Laa, Lbb, Lcc, and Ldd are the self-inductances of the stator windings. These self-inductances are a function of the rotor electrical angle, θe, and depend on the stator per-phase self-inductance, Ls, and the stator inductance fluctuation, Lm.
where θr is the rotor mechanical angle.
rotor offset is
pi/2if you define the rotor electrical angle with respect to the d-axis, or0if you define the rotor electrical angle with respect to the q-axis.Ls is the stator per-phase self-inductance. This value is the average self-inductance of each of the stator windings.
Lm is the stator inductance fluctuation. This value is the amount the self-inductance and mutual inductance fluctuate with the changing of the rotor angle.
Lab, Lac, Lba, and so on, are the mutual inductances of the stator windings. These mutual inductances are a function of the rotor electrical angle, θe, and depend on the stator mutual inductance, Ms, and the stator per-phase self-inductance, Ls.
Ms is the stator mutual inductance. This value is the average mutual inductance between the stator windings.
ψam, ψbm, ψcm, and ψdm are the permanent magnet fluxes linking the stator windings.
The permanent magnet flux linking winding a-a' is at maximum when θe = 0° and zero when θe = 90°. Therefore, the linked motor flux is defined by:
where ψm is the permanent magnet flux linkage.
Simplified Electrical Equations
To remove the rotor angle dependence for the inductive terms, you perform a transformation, T, on the motor equations.
The T transformation is defined by:
where θe is the electrical angle defined as Nθr. N is the number of pole pairs.
The transformation matrix has this pseudo-orthogonal property:
Using the T transformation on the stator winding voltages and currents transforms them to the dq0 and xy frames, which are independent of the rotor angle:
Applying this transformation to the first two electrical equations produces these equations
where:
Ld = Ls + Ms + 2 Lm. Ld is the stator d-axis inductance.
Lq = Ls + Ms − 2 Lm. Lq is the stator q-axis inductance.
L0 = Ls – 3Ms. L0 is the stator zero-sequence inductance.
ω is the rotor mechanical rotational speed.
N is the number of rotor permanent magnet pole pairs.
Alternative Flux Linkage Parameterization
You can parameterize the motor by using the back EMF or torque constants, which are more commonly given on motor datasheets, by using the Permanent magnet flux linkage parameter.
The back EMF constant is the peak voltage induced by the permanent magnet in the per-unit rotational speed of each of the phases. The relationship between the peak permanent magnet flux linkage and the back EMF is:
The back EMF, eph, for one phase is:
The torque constant is the peak torque induced by the per-unit current of each of the phases. It is numerically identical in value to the back EMF constant when both are expressed in SI units:
When Ld = Lq and the currents in all four phases are balanced, the combined torque T is:
where Ipk is the peak current in any of the four windings.
The factor 2 is calculated from the steady-state sum of the torques from all phases. Therefore, the torque constant kt can also be:
where T is the measured total torque when testing with a balanced four-phase current with a peak line voltage of Ipk. The RMS line voltage is:
Model Thermal Effects
You can expose thermal ports to model the effects of losses that convert power to heat. To expose the thermal ports, set the Modeling option parameter to either:
No thermal port— The block contains expanded electrical conserving ports associated with the stator windings, but does not contain thermal ports.Show thermal port— The block contains expanded electrical conserving ports associated with the stator windings and thermal conserving ports for each of the windings and for the rotor.
For more information about using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.
Variables
To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. You can specify nominal values using different sources, including the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
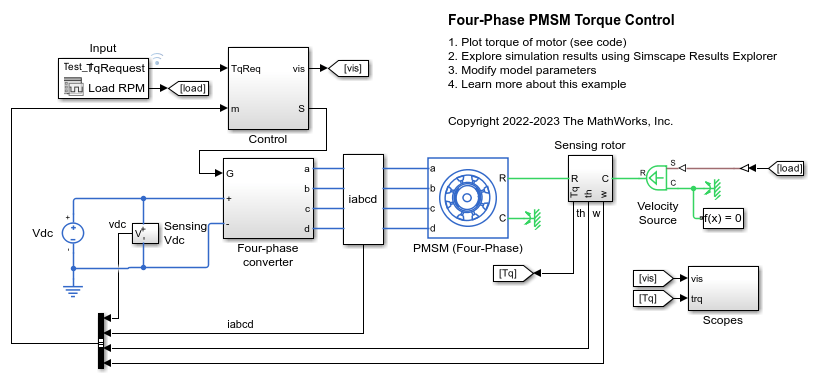
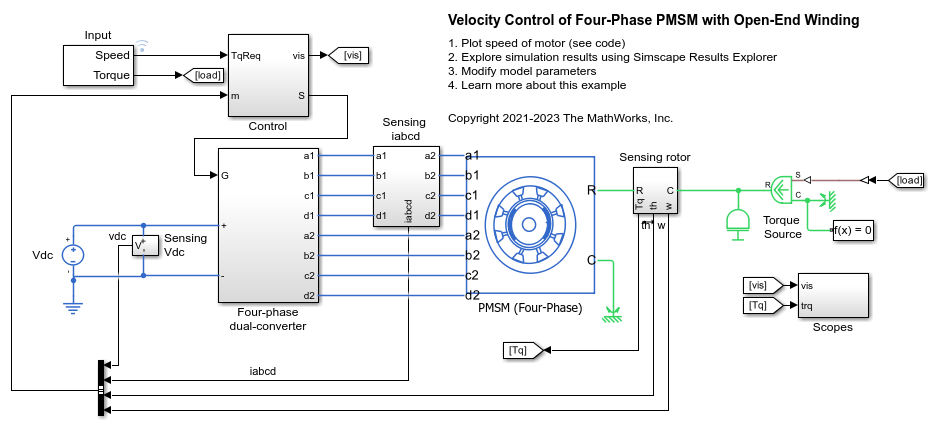
Examples
Ports
Conserving
Parameters
References
[1] Della Torre, F., et al. Symmetrical Components and Space-Vector Transformations for Four-Phase Networks. IEEE Transactions on Power Delivery, vol. 23, no. 4, pp.2191-200, Oct., 2008.
[2] Anderson, P. M. Analysis of Faulted Power Systems. IEEE Press Power Systems Engineering Series, 1995. ISBN 0-7803-1145-0.