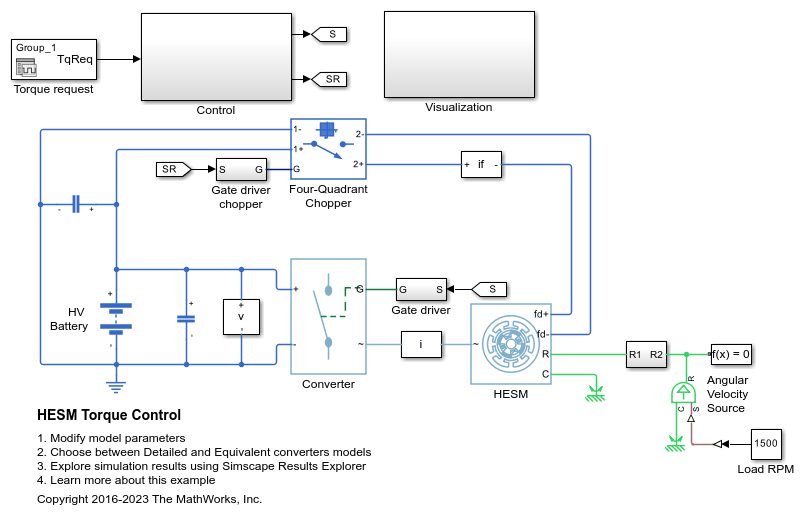
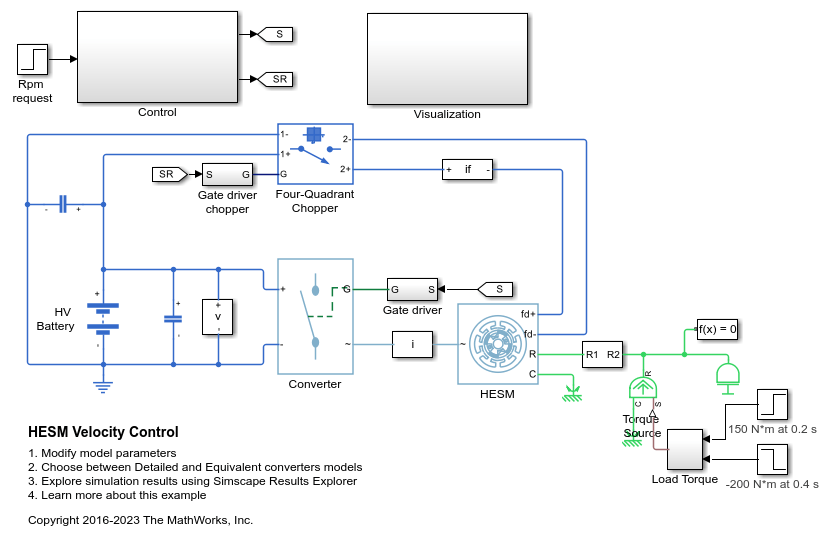
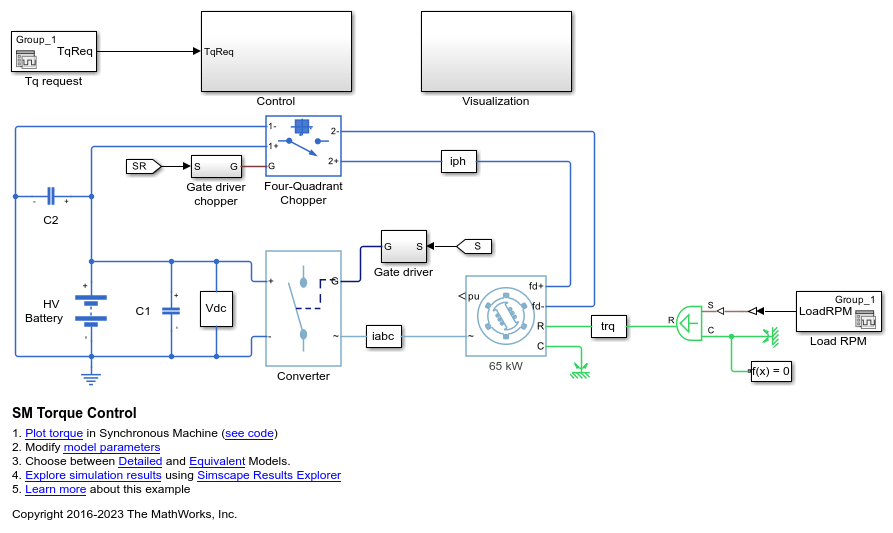
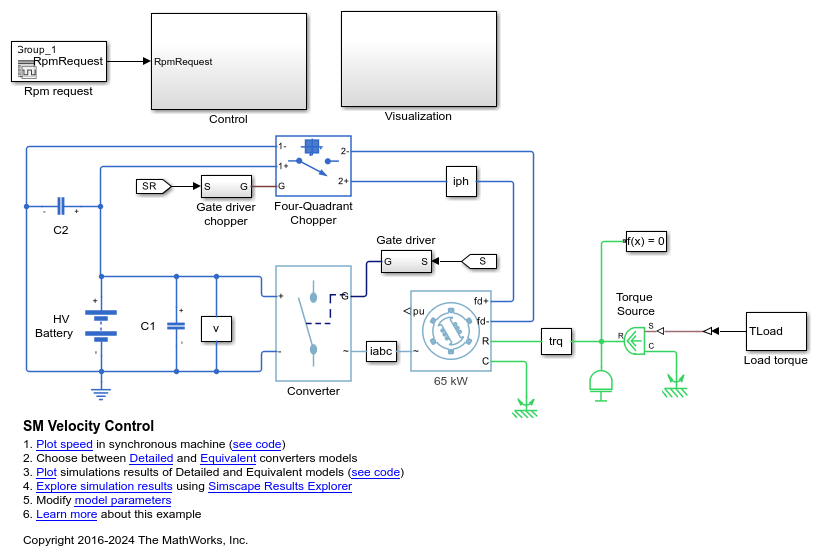
SM Current Controller

Discrete-time synchronous machine current PI controller

Libraries:
Simscape / Electrical / Control / SM Control

Description

The SM Current Controller block implements a discrete time PI-based synchronous machine (SM) current controller in the rotor d-q reference frame.

Defining Equations

The block is discretized using the backward Euler method due to its first-order simplicity and its stability.

Three PI current controllers implemented in the rotor reference frame produce the reference voltage vector:

$v_{d}^{r e f} = (K_{p_i d} + K_{i_i d} \frac{T_{s} z}{z - 1}) (i_{d}^{r e f} - i_{d}) + v_{d_F F},$

$v_{q}^{r e f} = (K_{p_i q} + K_{i_i q} \frac{T_{s} z}{z - 1}) (i_{q}^{r e f} - i_{q}) + v_{q_F F},$

and

$v_{f}^{r e f} = (K_{p_i f} + K_{i_i f} \frac{T_{s} z}{z - 1}) (i_{f}^{r e f} - i_{f}),$

where:

$v_{d}^{r e f}$ , $v_{q}^{r e f}$ , and $v_{f}^{r e f}$ are the d-axis, q-axis, and field reference voltages, respectively.
$i_{d}^{r e f}$ , $v_{q}^{r e f}$ , and $i_{f}^{r e f}$ are the d-axis, q-axis, and field reference currents, respectively.
$i_{d}$ , $i_{q}$ , and $i_{f}$ are the d-axis, q-axis, and field currents, respectively.
K_{p_id}, K_{p_iq}, and K_{p_if} are the proportional gains for the d-axis, q-axis and field controllers, respectively.
K_{i_id}, K_{i_iq}, and K_{i_if} are the integral gains for the d-axis, q-axis and field controllers, respectively.
v_{d_FF}, and v_{q_FF} are the feedforward voltages for the d-axis and q-axis, respectively, obtained from the machine mathematical equations and provided as inputs.
T_s, is the sample time of the discrete controller.

Using PI control results in a zero in the closed-loop transfer function which can be canceled by introducing a zero-cancelation block in the feedforward path. The zero cancellation transfer functions in discrete time are:

$G_{Z C_i d} (z) = \frac{\frac{T_{s} K_{i_i d}}{K_{p_i d}}}{z + (\frac{T_{s} - \frac{K_{p_i d}}{K_{i_i d}}}{\frac{K_{p_i d}}{K_{i_i d}}})},$

$G_{Z C_i q} (z) = \frac{\frac{T_{s} K_{i_i q}}{K_{p_i q}}}{z + (\frac{T_{s} - \frac{K_{p_i q}}{K_{i_i q}}}{\frac{K_{p_i q}}{K_{i_i q}}})},$

and

$G_{Z C_i f} (z) = \frac{\frac{T_{s} K_{i_i f}}{K_{p_i f}}}{z + (\frac{T_{s} - \frac{K_{p_i f}}{K_{i_i f}}}{\frac{K_{p_i f}}{K_{i_i f}}})} .$

Saturation must be imposed when the stator voltage vector exceeds the voltage phase limit V_{ph_max}:

$\sqrt{v_{d}^{2} + v_{q}^{2}} \leq V_{p h_m a x},$

where v_d, and v_q are the d-axis and q-axis voltages, respectively.

In the case of axis prioritization, the voltages v₁ and v₂ are introduced, where:

v₁ = v_d and v₂ = v_q for d-axis prioritization.
v₁ = v_q and v₂ = v_d for q-axis prioritization.

The constrained (saturated) voltages $v_{1}^{s a t}$ and $v_{2}^{s a t}$ are obtained as follows:

$v_{1}^{s a t} = min (\max (v_{1}^{u n s a t}, - V_{p h_m a x}), V_{p h_m a x}),$

and

$v_{2}^{s a t} = min (\max (v_{2}^{u n s a t}, - V_{2_m a x}), V_{2_m a x}),$

where:

$v_{1}^{u n s a t}$ and $v_{2}^{u n s a t}$ are the unconstrained (unsaturated) voltages.
v_{2_max} is the maximum value of v₂ that does not exceed the voltage phase limit, given by $v_{2_m a x} = \sqrt{{(V_{p h_m a x})}^{2} - {(v_{1}^{s a t})}^{2}} .$

In the case that the direct and quadrature axes have the same priority (d-q equivalence) the constrained voltages are obtained as follows:

$v_{d}^{s a t} = min (\max (v_{d}^{u n s a t}, - V_{d_m a x}), V_{d_m a x}),$

and

$v_{q}^{s a t} = min (\max (v_{q}^{u n s a t}, - V_{q_m a x}), V_{q_m a x}),$

where

$V_{d_m a x} = \frac{V_{p h_m a x} | v_{d}^{u n s a t} |}{\sqrt{{(v_{d}^{u n s a t})}^{2} + {(v_{q}^{u n s a t})}^{2}}},$

and

$V_{q_m a x} = \frac{V_{p h_m a x} | v_{q}^{u n s a t} |}{\sqrt{{(v_{d}^{u n s a t})}^{2} + {(v_{q}^{u n s a t})}^{2}}} .$

The constrained (saturated) field voltage $v_{f}^{s a t}$ is limited according to the maximum admissible value:

$v_{f}^{s a t} = min (\max (v_{f}^{u n s a t}, - V_{f_m a x}), V_{f_m a x}),$

where:

$v_{f}^{u n s a t}$ is the unconstrained (unsaturated) field voltage.
V_{f_max} is the maximum allowable field voltage.

An anti-windup mechanism is employed to avoid saturation of integrator output. In such a situation, the integrator gains become:

$K_{i_i d} + K_{a w_i d} (v_{d}^{s a t} - v_{d}^{u n s a t}),$

$K_{i_i q} + K_{a w_i q} (v_{q}^{s a t} - v_{q}^{u n s a t}),$

and

$K_{i_i f} + K_{a w_i f} (v_{f}^{s a t} - v_{f}^{u n s a t}),$

where K_{aw_id}, K_{aw_iq}, and K_{aw_if} are the anti-windup gains for the d-axis, q-axis and field controllers, respectively.

Assumptions

The plant model for direct and quadrature axis can be approximated with a first order system.
This control solution is used only for synchronous motors with sinusoidal flux distribution and field windings.

Examples

HESM Torque Control

Control the torque in a hybrid excitation synchronous machine (HESM) based electrical-traction drive. Permanent magnets and an excitation winding excite the HESM. A high-voltage battery feeds the SM through a controlled three-phase converter for the stator windings and through a controlled four quadrant chopper for the rotor winding. An ideal angular velocity source provides the load. The Control subsystem uses an open-loop approach to control the torque and a closed-loop approach to control the current. At each sample instant, the torque request is converted to relevant current references. The current control is PI-based. The simulation uses several torque steps in both the motor and generator modes. The Visualization subsystem contains scopes that allow you to see the simulation results.

Open Model

HESM Velocity Control

Control the rotor angular velocity in a hybrid excitation synchronous machine (HESM) based electrical-traction drive. Permanent magnets and an excitation winding excite the HESM. A high-voltage battery feeds the HESM through a controlled three-phase converter for the stator windings and through a controlled four quadrant chopper for the rotor winding. An ideal torque source provides the load. The Control subsystem includes a multi-rate PI-based cascade control structure. The control structure has an outer angular-velocity-control loop and three inner current-control loops. The Visualization subsystem contains scopes that allow you to see the simulation results.

Open Model

SM Torque Control

Control the torque in a synchronous machine (SM) based electrical-traction drive. A high-voltage battery feeds the SM through a controlled three-phase converter for the stator windings and a controlled four quadrant chopper for the rotor winding. An ideal angular velocity source provides the load. The Control subsystem uses an open-loop approach to control the torque and a closed-loop approach to control the current. At each sample instant, the torque request is converted to relevant current references. The current control is PI-based. The simulation uses several torque steps in both motor and generator modes. The task scheduling is implemented as a Stateflow® state machine. The Visualization subsystem contains scopes that allow you to see the simulation results.

Open Model

SM Velocity Control

Control the rotor angular velocity in a synchronous machine (SM) based electrical-traction drive. A high-voltage battery feeds the SM through a controlled three-phase converter for the stator windings and a controlled four quadrant chopper for the rotor winding. An ideal torque source provides the load. The Control subsystem includes a multi-rate PI-based cascade control structure which has an outer angular-velocity-control loop and three inner current-control loops. The task scheduling in the Control subsystem is implemented as a Stateflow® state machine. The Visualization subsystem contains scopes that allow you to see the simulation results.

Open Model

Ports