构建并仿真复合三相模型和扩展三相模型
在此示例中,您将构建并分析一个简单的 Simscape™ Electrical™ 模型,该模型仿真驱动纯电阻性三相负载的三相 AC 电压源的行为。然后,您将修改此模型中的负载,将其更改为:
无功三相负载
扩展为各个相的电阻性三相负载
每相的电阻不相等的扩展三相负载
要查看您在此示例中创建的完成的模型,请在 MATLAB® 命令提示符下输入 SimpleThreePhaseModel。
选择系统组件模块并构建电阻性三相模型
打开 Simulink® 起始页。在 MATLAB 的“主页”选项卡中,选择 Simulink 按钮。或者,在命令行中输入:
simulink
在 Simscape 部分中,查找为使用 Simscape Electrical 进行建模而预配置的模板。选择“电气三相”模板。一个包含以下模块的模型将在 Simulink 画布中打开。
模块
目的 库
Scope 显示三相系统的相电压和相电流。 Simulink > Sinks
Electrical Reference 为电气守恒端口提供接地连接。 Simscape > Foundation Library > Electrical > Electrical Elements
PS-Simulink Converter 将物理信号转换为 Simulink 信号。 Simscape > Utilities
Simulink-PS Converter 将 Simulink 信号转换为物理信号。 Simscape > Utilities
Solver Configuration 定义适用于所有物理建模模块的求解器设置。 Simscape > Utilities
Grounded Neutral (Three-Phase) 为三相系统的每个相提供电气接地连接。 Simscape > Electrical > Connectors & References
Line Voltage Sensor (Three-Phase) 测量三相系统的线间电压,并输出一个三元素物理信号向量。 Simscape > Electrical > Sensors & Transducers
该模型还包含两个链接,双击这些链接可以访问 Simscape 和 Simscape Electrical 库中的模块。有关通过 Simscape Electrical 使用模板进行建模的详细信息,请参阅Modeling Analog Circuit Architectures, Mechatronic Systems, and Electrical Power Systems Using Simscape Electrical。
删除 Simulink-PS Converter 和 Line Voltage Sensor (Three-Phase) 模块。
向模型中添加以下模块:
模块
目的 库
RLC (Three-Phase) 对三相负载的电阻、电感和电容属性进行建模。 Simscape > Electrical > Passive > RLC Assemblies
Current Sensor (Three-Phase) 将三相负载每相的电流转换为与该电流成比例的物理信号。 Simscape > Electrical > Sensors & Transducers
Phase Voltage Sensor (Three-Phase) 将三相系统每相两端的电压转换为与该电压成比例的物理信号。 Simscape > Electrical > Sensors & Transducers
Voltage Source (Three-Phase) 提供理想的三相电压源,无论该电压源中流过的电流多大,它都能保持其输出端子上的正弦电压不变。 Simscape > Electrical > Sources
通过右键点击 PS-Simulink Converter 和 Grounded-Neutral (Three-Phase) 模块并将它们拖动到画布上的新位置来复制这两个模块。
通过点击 Scope 模块的输入端并选择出现的交互式提示,为该模块添加第二个输入端口。
按下图所示连接各模块。
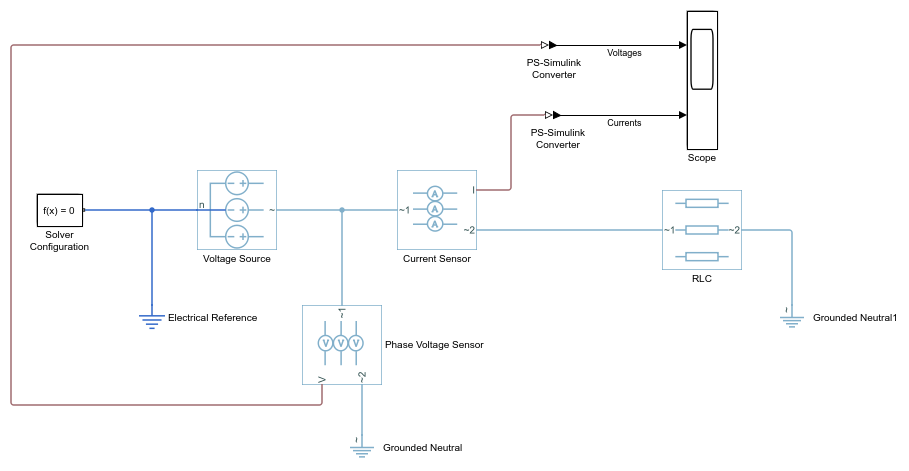
删除画布上标题为“打开 Simscape 库”和“打开 Simscape Electrical 库”的注解。使用名称
MySimpleThreePhaseModel保存模型。此模型中的模块使用复合三相端口。有关详细信息,请参阅Three-Phase Ports。
指定仿真参数
与 Simscape 模型一样,每个独特拓扑物理网络中都必须包含一个 Solver Configuration 模块。此模型只有一个物理网络,因此只需使用一个 Solver Configuration 模块。
在 Solver Configuration 模块中,选择使用局部求解器,并将采样时间设置为
0.0001。在基于 Simscape 的模型中,局部求解器是一种基于采样的求解器,它将物理网络状态表示为离散状态。对于大多数 Simscape Electrical 模型,局部求解器是合适的首选。每经过一个仿真时间步,求解器都会更新一次模块状态,该时间步是由采样时间决定的。对于 60-Hz AC 系统的仿真,合适的采样时间值以
1e-4为数量级。有关求解器选项的详细信息,请参阅 Solver Configuration。如果您更愿意使用连续求解器而非离散求解器,请清除 Solver Configuration 模块中的使用局部求解器复选框。然后,仿真将使用模型配置参数(建模 > 模型设置)中指定的 Simulink 求解器。对于 Simscape Electrical 模型,合适的求解器选择是中等刚性求解器 ode23t。对于 60 Hz AC 系统,请将最大步长值指定为
1e-4的数量级。有关详细信息,请参阅Variable-Step Continuous Explicit Solvers。在 Simulink 编辑器中,将仿真停止时间设置为
0.1。
负载阻抗参数
RLC 模块对三相负载的电阻、电感和电容特性进行建模。使用组件结构参数,您可以指定电阻、电感和电容的串联或并联组合。
在 RLC 模块中,默认值为:
组件结构 -
R。电阻 -
1Ω。
使用默认的组件结构值 R,对纯电阻性的三相负载进行建模。每相的电阻为 1 Ω。
指定显示参数
模型中的传感器模块将三相系统每相的电流和电压转换为成比例的物理信号。PS-Simulink Converter 模块将这些物理信号转换为 Simulink 信号,供 Scope 模块显示。
在这三种类型的模块中,只有转换器模块具有参数。对于此示例:
将 PS-Simulink Converter1 模块的输出信号单位设置为
V。此设置可确保该模块输出的信号与输入的电压信号具有相同的幅值。将 PS-Simulink Converter2 模块的输出信号单位设置为
A。此设置可确保该模块输出的信号与输入的电流信号具有相同的幅值。
为 Scope 模块的输入信号添加标签。双击每条信号线,按照模型图所示,输入相应的标签
Voltages或Currents。
现在,您便可以仿真模型并分析结果了。
仿真并分析电阻性三相模型
保存模型。
对模型进行仿真。
查看相电流和相电压。双击 Scope 模块。
在示波器菜单中,选择视图 > 配置属性。将布局设置为 1×2 显示。
要根据数据缩放示波器坐标区,请点击自动缩放按钮
 。
。
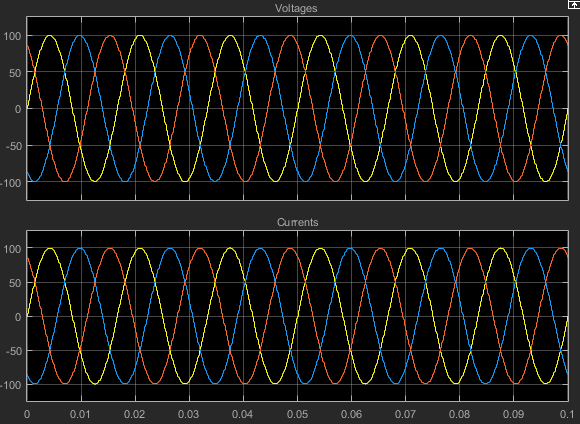
在此仿真中,RLC (Three-Phase) 模块的组件结构参数指定三相负载的电气特性为纯电阻性。因此,对于三相系统的每相,电压和电流保持彼此同相。由于每相的电阻均为 1 Ω,因此相电压的幅值等于相电流的幅值。
仿真并分析无功三相模型
您可以修改模型以创建无功负载。无功负载具有电感或电容特性。
使用名称
SimpleThreePhaseModelReactive保存此版本的模型。在 RLC (Three-Phase) 模块中:
将组件结构设置为
Series RL将电感设置为
0.002
对模型进行仿真。
查看仿真结果。自动缩放示波器坐标区。
更详细地检查结果。例如,点击“缩放”按钮
 ,然后在其中一个图的前三分之一处拖动一个框。
,然后在其中一个图的前三分之一处拖动一个框。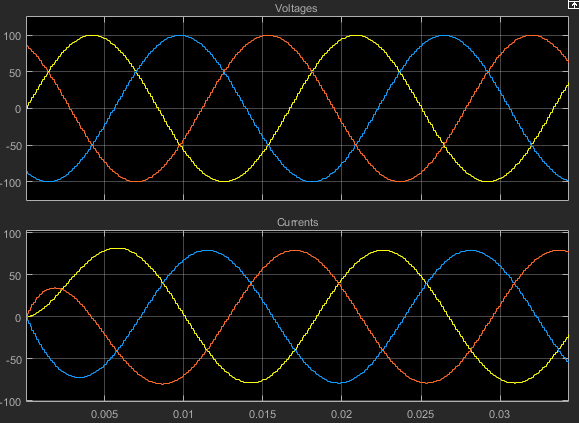
三相负载的电气特性不再是纯电阻性的。由于负载具有电感特性,因此每相的电流滞后于电压。
创建扩展的平衡三相模型
打开您最初创建的电阻性三相模型
MySimpleThreePhaseModel。删除 RLC (Three-Phase) 模块。
从 Simscape > Electrical > Connectors & References 库中,将 Phase Splitter 模块的两个副本拖入模型中。
将其中一个 Phase Splitter 模块水平翻转。选择该模块。在工具条的格式选项卡上,点击左右翻转
 。
。从 Simscape > Foundation Library > Electrical > Electrical Elements 库中,将一个 Resistor 元件拖入模型中。
为了给更多组件腾出空间,可隐藏 Resistor 元件标签。右键点击该电阻器,选择格式 > 显示模块名称以清除此选项。
再制作 Resistor 元件的两个副本。
按图所示连接各组件。
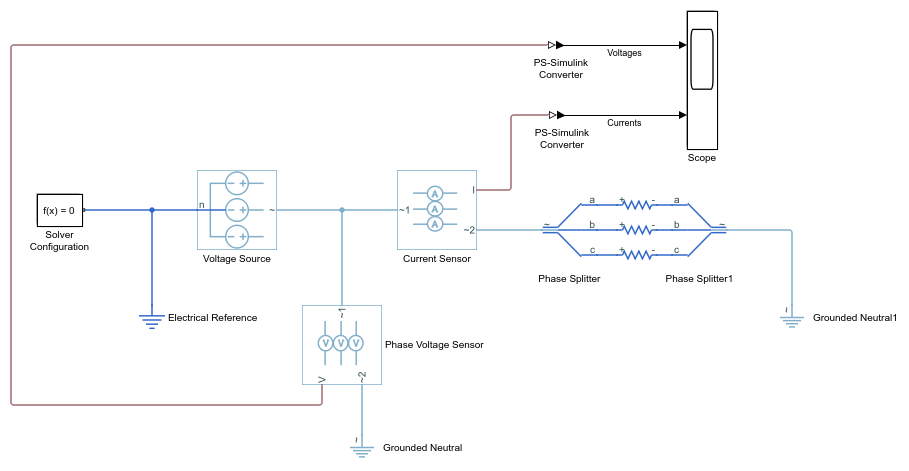
使用名称
SimpleThreePhaseModelExpandedBalanced保存此版本的修改后模型。此模型名称反映了先前通过 RLC 模块建模的负载现在已扩展为各个相。负载仍然是平衡的,即每相的电阻相等。
创建扩展的非平衡三相模型
通过更改一相的电阻,使
SimpleThreePhaseModelExpandedBalanced中的负载不平衡。双击 c 相电阻器元件。将电阻 更改为2。使用名称
SimpleThreePhaseModelExpandedUnbalanced保存此版本的修改后模型。此模型名称反映了先前通过 RLC 模块建模的三相负载已扩展为各个相。负载是不平衡的,即其中一相的电阻高于其他两相。
仿真扩展的平衡和非平衡模型并分析结果
对
SimpleThreePhaseModelExpandedBalanced模型进行仿真。在 Simulink 资源管理器的菜单栏中,点击运行按钮。查看仿真结果。双击 Scope 模块。
要根据数据缩放示波器坐标区,请点击自动缩放按钮
 。
。
在
SimpleThreePhaseModel中,RLC (Three-Phase) 模块的组件结构参数指定三相负载为纯电阻性负载。在此版本的模型中,负载已扩展为每相一个单独的电阻元件,但每相的电阻保持不变。对于三相系统的每相,电压和电流保持彼此同相。由于每相的电阻均为1Ω,因此相电压的幅值等于相电流的幅值。通过将这些结果与三相电阻性模型的结果进行比较,我们可以看到,具有复合三相端口的模块(原始模型中的 RLC (Three-Phase) 模块)所产生的结果与扩展相模型的结果具有相同的保真度。
打开
SimpleThreePhaseModelExpandedUnbalanced模型。对模型进行仿真。自动缩放示波器坐标区。
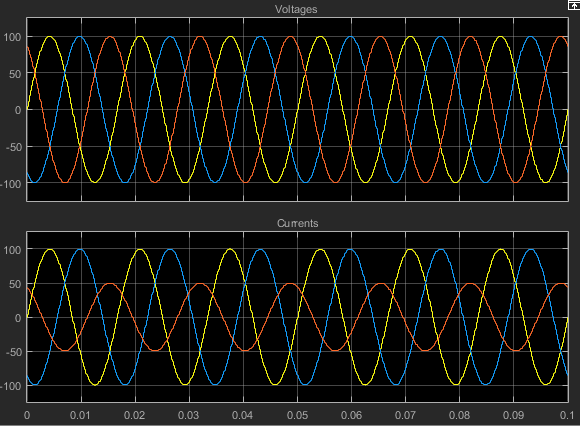
在此版本的模型中,三相负载的 c 相电阻是其他两相的两倍。因此,该相的电流为其他两相的一半,如第二个图所示。然而,由于负载仍然是纯电阻性的,电压和电流保持彼此同相。