anova2
Two-way analysis of variance
Syntax
Description
anova2 performs two-way analysis
of variance (ANOVA) with balanced designs. To perform two-way ANOVA
with unbalanced designs, see anovan.
p = anova2(y,reps)y.
reps is the number of replicates for each
combination of factor groups, which must be constant, indicating a
balanced design. For unbalanced designs, use anovan.
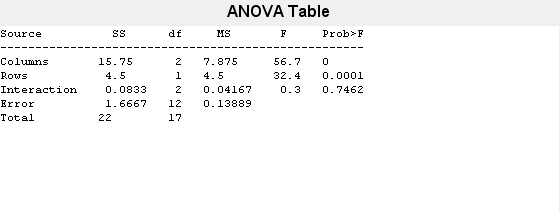
The anova2 function tests the main effects for
column and row factors and their interaction effect. To test the interaction
effect, reps must be greater than 1.
anova2 also displays the standard ANOVA
table.
p = anova2(y,reps,displayopt)displayopt is 'on' (default)
and suppresses the display when displayopt is 'off'.
[ returns a p,tbl,stats]
= anova2(___)stats structure,
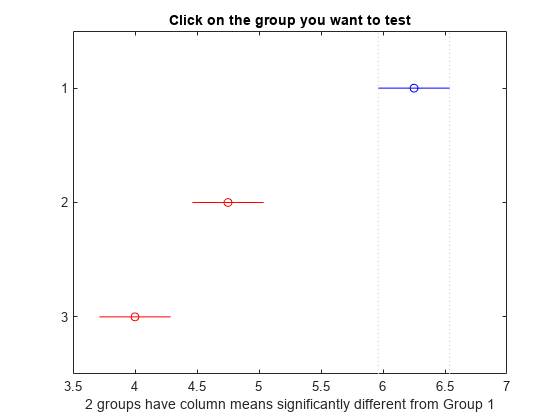
which you can use to perform a multiple comparison test. A multiple
comparison test enables you to determine which pairs of group means
are significantly different. To perform this test, use multcompare, providing the stats structure
as input.
Examples
Input Arguments
Output Arguments
Alternative Functionality
Instead of using anova2, you can create an anova
object by using the anova function.
The anova function provides these advantages:
The
anovafunction allows you to specify the ANOVA model type, sum of squares type, and factors to treat as categorical.anovaalso supports table predictor and response input arguments.In addition to the outputs returned by
anova2, the properties of theanovaobject contain the following:ANOVA model formula
Fitted ANOVA model coefficients
Residuals
Factors and response data
The
anovaobject functions allow you to conduct further analysis after fitting theanovaobject. For example, you can create an interactive plot of multiple comparisons of means for the ANOVA, get the mean response estimates for each value of a factor, and calculate the variance component estimates.
References
[1] Hogg, R. V., and J. Ledolter. Engineering Statistics. New York: MacMillan, 1987.
Version History
Introduced before R2006a
See Also
anova | anova1 | anovan | multcompare