Bayesian Optimization with Tall Arrays

This example uses:

This example shows how to use Bayesian optimization to select optimal parameters for training a kernel classifier by using the 'OptimizeHyperparameters' name-value argument. The sample data set airlinesmall.csv is a large data set that contains a tabular file of airline flight data. This example creates a tall table containing the data, and extracts class labels and predictor data from the tall table to run the optimization procedure.

When you perform calculations on tall arrays, MATLAB® uses either a parallel pool (default if you have Parallel Computing Toolbox™) or the local MATLAB session. If you want to run the example using the local MATLAB session when you have Parallel Computing Toolbox, you can change the global execution environment by using the mapreducer function.

Get Data into MATLAB®

Create a datastore that references the folder location with the data. The data can be contained in a single file, a collection of files, or an entire folder. For folders that contain a collection of files, you can specify the entire folder location, or use the wildcard character, '*.csv', to include multiple files with the same file extension in the datastore. Select a subset of the variables to work with, and treat 'NA' values as missing data so that datastore replaces them with NaN values. Create a tall table that contains the data in the datastore.

ds = datastore('airlinesmall.csv');
ds.SelectedVariableNames = {'Month','DayofMonth','DayOfWeek',...
                            'DepTime','ArrDelay','Distance','DepDelay'};
ds.TreatAsMissing = 'NA';
tt  = tall(ds) % Tall table

Starting parallel pool (parpool) using the 'Processes' profile ...
Connected to parallel pool with 6 workers.

tt =

  M×7 tall table

    Month    DayofMonth    DayOfWeek    DepTime    ArrDelay    Distance    DepDelay
    _____    __________    _________    _______    ________    ________    ________

     10          21            3          642          8         308          12   
     10          26            1         1021          8         296           1   
     10          23            5         2055         21         480          20   
     10          23            5         1332         13         296          12   
     10          22            4          629          4         373          -1   
     10          28            3         1446         59         308          63   
     10           8            4          928          3         447          -2   
     10          10            6          859         11         954          -1   
      :          :             :           :          :           :           :
      :          :             :           :          :           :           :

Prepare Class Labels and Predictor Data

Determine the flights that are late by 10 minutes or more by defining a logical variable that is true for a late flight. This variable contains the class labels. A preview of this variable includes the first few rows.

Y = tt.DepDelay > 10 % Class labels

Y =

  M×1 tall logical array

   1
   0
   1
   1
   0
   1
   0
   0
   :
   :

Create a tall array for the predictor data.

X = tt{:,1:end-1} % Predictor data

X =

  M×6 tall double matrix

          10          21           3         642           8         308
          10          26           1        1021           8         296
          10          23           5        2055          21         480
          10          23           5        1332          13         296
          10          22           4         629           4         373
          10          28           3        1446          59         308
          10           8           4         928           3         447
          10          10           6         859          11         954
          :           :            :          :           :           :
          :           :            :          :           :           :

Remove rows in X and Y that contain missing data.

R = rmmissing([X Y]); % Data with missing entries removed
X = R(:,1:end-1); 
Y = R(:,end);

Perform Bayesian Optimization Using `OptimizeHyperparameters`

Optimize hyperparameters using the 'OptimizeHyperparameters' name-value argument.

Standardize the predictor variables.

Z = zscore(X);

Find the optimal values for the 'KernelScale' and 'Lambda' name-value arguments that minimize the loss on the holdout validation set. By default, the software selects and reserves 20% of the data as validation data, and trains the model using the rest of the data. You can change the holdout fraction by using the 'HyperparameterOptimizationOptions' name-value argument. For reproducibility, use the 'expected-improvement-plus' acquisition function and set the seeds of the random number generators using rng and tallrng. The results can vary depending on the number of workers and the execution environment for the tall arrays. For details, see Control Where Your Code Runs.

rng('default') 
tallrng('default')
Mdl = fitckernel(Z,Y,'Verbose',0,'OptimizeHyperparameters', ...
    {'KernelScale','Lambda'},'HyperparameterOptimizationOptions', ...
    struct('AcquisitionFunctionName','expected-improvement-plus'))

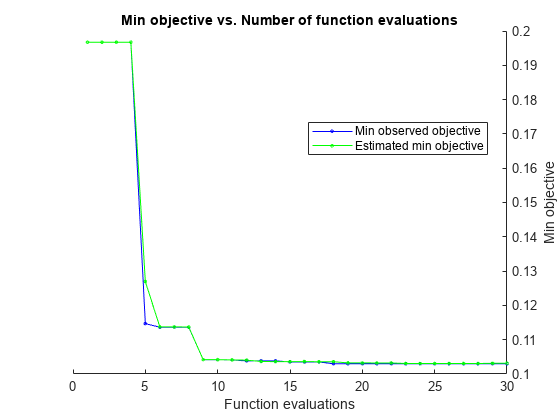
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 2: Completed in 6.4 sec
- Pass 2 of 2: Completed in 1.9 sec
Evaluation completed in 9.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.8 sec
Evaluation completed in 1.9 sec
|=====================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |  KernelScale |       Lambda |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|    1 | Best   |     0.19672 |      83.403 |     0.19672 |     0.19672 |       1.2297 |    0.0080902 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.94 sec
Evaluation completed in 1.1 sec
|    2 | Accept |     0.19672 |      35.532 |     0.19672 |     0.19672 |     0.039643 |   2.5756e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.97 sec
Evaluation completed in 1.1 sec
|    3 | Accept |     0.19672 |      35.184 |     0.19672 |     0.19672 |      0.02562 |   1.2555e-08 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.83 sec
Evaluation completed in 0.93 sec
|    4 | Accept |     0.19672 |      34.375 |     0.19672 |     0.19672 |       92.644 |   1.2056e-07 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.86 sec
Evaluation completed in 0.96 sec
|    5 | Best   |     0.11469 |      55.874 |     0.11469 |     0.12698 |       11.173 |   0.00024836 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.86 sec
Evaluation completed in 0.97 sec
|    6 | Best   |     0.11365 |      50.865 |     0.11365 |     0.11373 |       10.609 |   0.00025761 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.92 sec
Evaluation completed in 1 sec
|    7 | Accept |     0.19672 |        34.5 |     0.11365 |     0.11373 |    0.0059498 |   0.00043861 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.86 sec
Evaluation completed in 0.95 sec
|    8 | Accept |     0.12122 |      56.119 |     0.11365 |     0.11371 |        11.44 |   0.00045722 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.96 sec
Evaluation completed in 1.1 sec
|    9 | Best   |     0.10417 |      28.379 |     0.10417 |     0.10417 |       8.0424 |   6.7998e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.82 sec
Evaluation completed in 0.92 sec
|   10 | Accept |     0.10433 |      27.657 |     0.10417 |     0.10417 |       9.6694 |   1.4948e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.9 sec
Evaluation completed in 0.99 sec
|   11 | Best   |     0.10409 |      27.999 |     0.10409 |     0.10411 |       6.2099 |   6.1093e-06 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.84 sec
Evaluation completed in 0.93 sec
|   12 | Best   |     0.10383 |      29.942 |     0.10383 |     0.10404 |       5.6767 |   7.6134e-08 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.84 sec
Evaluation completed in 0.93 sec
|   13 | Accept |     0.10408 |      30.076 |     0.10383 |     0.10365 |       8.1769 |   8.5993e-09 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.87 sec
Evaluation completed in 0.96 sec
|   14 | Accept |     0.10404 |      28.263 |     0.10383 |     0.10361 |       7.6191 |   6.4079e-07 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.88 sec
Evaluation completed in 0.98 sec
|   15 | Best   |     0.10351 |      28.352 |     0.10351 |     0.10362 |       4.2987 |   9.2645e-08 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.86 sec
Evaluation completed in 0.95 sec
|   16 | Accept |     0.10404 |      29.934 |     0.10351 |     0.10362 |       4.8747 |   1.7838e-08 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.92 sec
Evaluation completed in 1 sec
|   17 | Accept |     0.10657 |      57.566 |     0.10351 |     0.10357 |       4.8239 |   0.00016344 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.85 sec
Evaluation completed in 0.94 sec
|   18 | Best   |     0.10299 |      28.692 |     0.10299 |     0.10358 |       3.5555 |   2.7165e-06 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.89 sec
Evaluation completed in 0.99 sec
|   19 | Accept |     0.10366 |      28.388 |     0.10299 |     0.10324 |       3.8035 |   1.3542e-06 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.86 sec
Evaluation completed in 0.95 sec
|   20 | Accept |     0.10337 |      28.643 |     0.10299 |     0.10323 |        3.806 |   1.8101e-06 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.88 sec
Evaluation completed in 0.97 sec
|=====================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |  KernelScale |       Lambda |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|   21 | Accept |     0.10345 |      28.972 |     0.10299 |     0.10322 |       3.3655 |    9.082e-09 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.86 sec
Evaluation completed in 0.95 sec
|   22 | Accept |     0.19672 |      36.972 |     0.10299 |     0.10322 |       999.62 |   1.2609e-06 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.86 sec
Evaluation completed in 0.96 sec
|   23 | Accept |     0.10315 |      28.377 |     0.10299 |     0.10306 |       3.6716 |   1.2445e-08 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.92 sec
Evaluation completed in 1 sec
|   24 | Accept |     0.19672 |      34.383 |     0.10299 |     0.10306 |    0.0010004 |   2.6214e-08 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.92 sec
Evaluation completed in 1 sec
|   25 | Accept |     0.19672 |      33.973 |     0.10299 |     0.10306 |      0.21865 |    0.0026529 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.84 sec
Evaluation completed in 0.95 sec
|   26 | Accept |     0.19672 |      36.951 |     0.10299 |     0.10306 |       299.92 |    0.0032109 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.93 sec
Evaluation completed in 1 sec
|   27 | Accept |     0.19672 |      34.099 |     0.10299 |     0.10306 |     0.002436 |    0.0040428 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.2 sec
Evaluation completed in 1.4 sec
|   28 | Accept |     0.19672 |      36.694 |     0.10299 |     0.10305 |      0.50559 |   3.3667e-08 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.88 sec
Evaluation completed in 0.97 sec
|   29 | Accept |     0.10354 |      30.402 |     0.10299 |     0.10313 |       3.7754 |   9.5626e-09 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.84 sec
Evaluation completed in 0.92 sec
|   30 | Accept |     0.10405 |      27.686 |     0.10299 |     0.10315 |       8.9864 |   2.3136e-07 |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 1102.4884 seconds

Figure contains an axes object. The axes object with title Min objective vs. Number of function evaluations, xlabel Function evaluations, ylabel Min objective contains 2 objects of type line. These objects represent Min observed objective, Estimated min objective.

Figure contains an axes object. The axes object with title Objective function model, xlabel KernelScale, ylabel Lambda contains 5 objects of type line, surface, contour. One or more of the lines displays its values using only markers These objects represent Observed points, Model mean, Next point, Model minimum feasible.

Total objective function evaluation time: 1088.2513

Best observed feasible point:
    KernelScale      Lambda  
    ___________    __________

      3.5555       2.7165e-06

Observed objective function value = 0.10299
Estimated objective function value = 0.10332
Function evaluation time = 28.6921

Best estimated feasible point (according to models):
    KernelScale      Lambda  
    ___________    __________

      3.6716       1.2445e-08

Estimated objective function value = 0.10315
Estimated function evaluation time = 29.1903

Mdl = 
  ClassificationKernel
            PredictorNames: {'x1'  'x2'  'x3'  'x4'  'x5'  'x6'}
              ResponseName: 'Y'
                ClassNames: [0 1]
                   Learner: 'svm'
    NumExpansionDimensions: 256
               KernelScale: 3.6716
                    Lambda: 1.2445e-08
             BoxConstraint: 665.9442


  Properties, Methods

Perform Bayesian Optimization by Using `bayesopt`

Alternatively, you can use the bayesopt function to find the optimal values of hyperparameters.

Split the data set into training and test sets. Specify a 1/3 holdout sample for the test set.

rng('default') % For reproducibility
tallrng('default') % For reproducibility
Partition = cvpartition(Y,'Holdout',1/3);
trainingInds = training(Partition); % Indices for the training set
testInds = test(Partition);         % Indices for the test set

Extract training and testing data and standardize the predictor data.

Ytrain = Y(trainingInds); % Training class labels
Xtrain = X(trainingInds,:);
[Ztrain,mu,stddev] = zscore(Xtrain); % Standardized training data

Ytest = Y(testInds); % Testing class labels
Xtest = X(testInds,:);
Ztest = (Xtest-mu)./stddev; % Standardized test data

Define the variables sigma and lambda to find the optimal values for the 'KernelScale' and 'Lambda' name-value arguments. Use optimizableVariable and specify a wide range for the variables because optimal values are unknown. Apply logarithmic transformation to the variables to search for the optimal values on a log scale.

N = gather(numel(Ytrain)); % Evaluate the length of the tall training array in memory

Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.85 sec
Evaluation completed in 0.99 sec

sigma = optimizableVariable('sigma',[1e-3,1e3],'Transform','log');
lambda = optimizableVariable('lambda',[(1e-3)/N, (1e3)/N],'Transform','log');

Create the objective function for Bayesian optimization. The objective function takes in a table that contains the variables sigma and lambda, and then computes the classification loss value for the binary Gaussian kernel classification model trained using the fitckernel function. Set 'Verbose',0 within fitckernel to suppress the iterative display of diagnostic information.

minfn = @(z)gather(loss(fitckernel(Ztrain,Ytrain, ...
    'KernelScale',z.sigma,'Lambda',z.lambda,'Verbose',0), ...
    Ztest,Ytest));

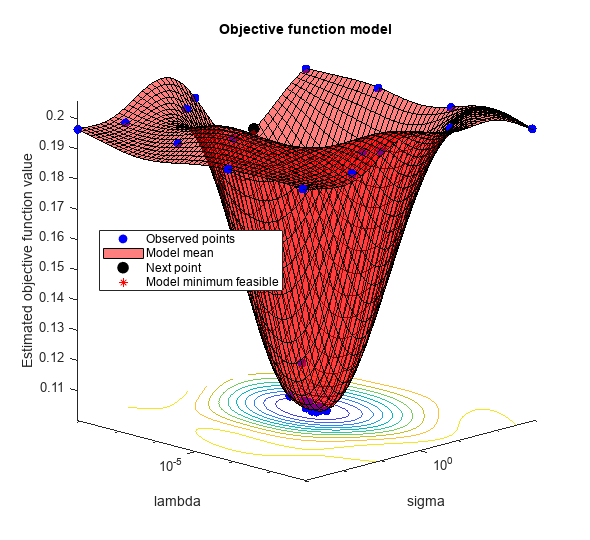
Optimize the parameters [sigma,lambda] of the kernel classification model with respect to the classification loss by using bayesopt. By default, bayesopt displays iterative information about the optimization at the command line. For reproducibility, set the AcquisitionFunctionName option to 'expected-improvement-plus'. The default acquisition function depends on run time and, therefore, can give varying results.

results = bayesopt(minfn,[sigma,lambda], ...
    'AcquisitionFunctionName','expected-improvement-plus')

Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|=====================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |        sigma |       lambda |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|    1 | Best   |     0.19651 |      55.774 |     0.19651 |     0.19651 |       1.2297 |     0.012135 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|    2 | Accept |     0.19651 |      77.257 |     0.19651 |     0.19651 |     0.039643 |   3.8633e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|    3 | Accept |     0.19651 |      54.632 |     0.19651 |     0.19651 |      0.02562 |   1.8832e-08 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.99 sec
Evaluation completed in 1.1 sec
|    4 | Accept |     0.19651 |       30.84 |     0.19651 |     0.19651 |       92.644 |   1.8084e-07 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.1 sec
|    5 | Accept |     0.19651 |      31.653 |     0.19651 |     0.19651 |       978.95 |   0.00015066 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|    6 | Accept |     0.19651 |      62.207 |     0.19651 |     0.19651 |    0.0089609 |    0.0059189 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|    7 | Accept |     0.19651 |      68.693 |     0.19651 |     0.19651 |    0.0010015 |   1.4474e-08 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|    8 | Accept |     0.19651 |      53.736 |     0.19651 |     0.19651 |      0.27475 |    0.0044831 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|    9 | Accept |     0.19651 |      58.473 |     0.19651 |     0.19651 |      0.81326 |   1.0753e-07 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|   10 | Accept |     0.19651 |      68.878 |     0.19651 |     0.19651 |    0.0040507 |   0.00011333 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.99 sec
Evaluation completed in 1.1 sec
|   11 | Accept |     0.19651 |      31.761 |     0.19651 |     0.19651 |       980.38 |    1.362e-08 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.98 sec
Evaluation completed in 1.1 sec
|   12 | Accept |     0.19651 |      31.332 |     0.19651 |     0.19651 |       968.03 |     0.011653 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.2 sec
Evaluation completed in 1.3 sec
|   13 | Accept |     0.19651 |      60.755 |     0.19651 |     0.19651 |      0.41617 |   1.6704e-07 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.1 sec
|   14 | Best   |     0.10059 |      25.589 |     0.10059 |      0.1006 |       2.9545 |   2.4479e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.3 sec
|   15 | Accept |     0.10098 |      24.933 |     0.10059 |      0.1006 |       5.3367 |   2.7906e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 2.1 sec
Evaluation completed in 2.3 sec
|   16 | Accept |     0.10101 |      30.013 |     0.10059 |      0.1006 |        4.233 |   1.4951e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|   17 | Best   |     0.10049 |      28.908 |     0.10049 |     0.10013 |       4.0225 |   2.3847e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.1 sec
|   18 | Accept |     0.10076 |      26.625 |     0.10049 |     0.10032 |       3.7144 |   1.9977e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.2 sec
Evaluation completed in 1.3 sec
|   19 | Accept |     0.10061 |      29.056 |     0.10049 |     0.10025 |       3.5125 |   4.2084e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|   20 | Accept |     0.10056 |      26.932 |     0.10049 |     0.10029 |       3.7269 |   2.7754e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.1 sec
|=====================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |        sigma |       lambda |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|   21 | Accept |     0.10089 |       25.84 |     0.10049 |     0.10044 |       3.8681 |   2.9799e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.1 sec
|   22 | Accept |     0.10101 |      25.461 |     0.10049 |     0.10052 |       6.1914 |   8.6976e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|   23 | Accept |     0.10161 |      27.882 |     0.10049 |     0.10053 |       5.1566 |   5.2959e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.1 sec
|   24 | Accept |      0.1028 |      61.428 |     0.10049 |     0.10053 |       3.8952 |   0.00012578 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.99 sec
Evaluation completed in 1.1 sec
|   25 | Accept |     0.11158 |       50.54 |     0.10049 |     0.10053 |        12.25 |   0.00018879 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.95 sec
Evaluation completed in 1 sec
|   26 | Best   |     0.10014 |      25.922 |     0.10014 |     0.10042 |       3.5501 |    2.292e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|   27 | Accept |     0.19651 |      70.888 |     0.10014 |     0.10042 |    0.0010185 |   1.3606e-06 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|   28 | Accept |     0.10103 |      24.309 |     0.10014 |     0.10053 |       3.4712 |   2.1357e-05 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.1 sec
|   29 | Accept |     0.19651 |      32.212 |     0.10014 |     0.10053 |       980.28 |   1.8241e-06 |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.2 sec
|   30 | Accept |     0.19651 |      66.958 |     0.10014 |     0.10053 |    0.0010035 |     0.011867 |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 1361.76 seconds
Total objective function evaluation time: 1289.4879

Best observed feasible point:
    sigma      lambda  
    ______    _________

    3.5501    2.292e-05

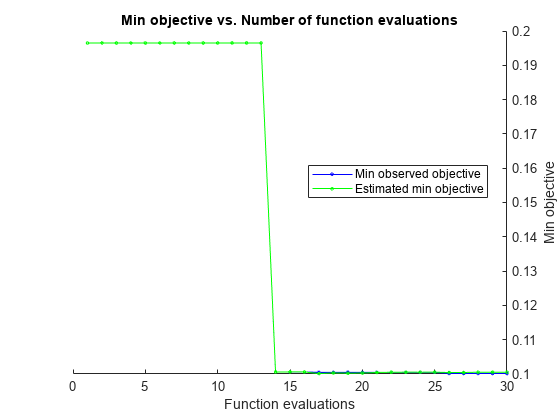
Observed objective function value = 0.10014
Estimated objective function value = 0.10053
Function evaluation time = 25.9216

Best estimated feasible point (according to models):
    sigma      lambda  
    ______    _________

    3.5501    2.292e-05

Estimated objective function value = 0.10053
Estimated function evaluation time = 26.7715

Figure contains an axes object. The axes object with title Objective function model, xlabel sigma, ylabel lambda contains 5 objects of type line, surface, contour. One or more of the lines displays its values using only markers These objects represent Observed points, Model mean, Next point, Model minimum feasible.

results = 
  BayesianOptimization with properties:

                      ObjectiveFcn: @(z)gather(loss(fitckernel(Ztrain,Ytrain,'KernelScale',z.sigma,'Lambda',z.lambda,'Verbose',0),Ztest,Ytest))
              VariableDescriptions: [1×2 optimizableVariable]
                           Options: [1×1 struct]
                      MinObjective: 0.1001
                   XAtMinObjective: [1×2 table]
             MinEstimatedObjective: 0.1005
          XAtMinEstimatedObjective: [1×2 table]
           NumObjectiveEvaluations: 30
                  TotalElapsedTime: 1.3618e+03
                         NextPoint: [1×2 table]
                            XTrace: [30×2 table]
                    ObjectiveTrace: [30×1 double]
                  ConstraintsTrace: []
                     UserDataTrace: {30×1 cell}
      ObjectiveEvaluationTimeTrace: [30×1 double]
                IterationTimeTrace: [30×1 double]
                        ErrorTrace: [30×1 double]
                  FeasibilityTrace: [30×1 logical]
       FeasibilityProbabilityTrace: [30×1 double]
               IndexOfMinimumTrace: [30×1 double]
             ObjectiveMinimumTrace: [30×1 double]
    EstimatedObjectiveMinimumTrace: [30×1 double]

Return the best feasible point in the Bayesian model results by using the bestPoint function. Use the default criterion min-visited-upper-confidence-interval, which determines the best feasible point as the visited point that minimizes an upper confidence interval on the objective function value.

zbest = bestPoint(results)

zbest=1×2 table
    sigma      lambda  
    ______    _________

    3.5501    2.292e-05

The table zbest contains the optimal estimated values for the 'KernelScale' and 'Lambda' name-value arguments. You can specify these values when training a new optimized kernel classifier by using

Mdl = fitckernel(Ztrain,Ytrain,'KernelScale',zbest.sigma,'Lambda',zbest.lambda)

For tall arrays, the optimization procedure can take a long time. If the data set is too large to run the optimization procedure, you can try to optimize the parameters by using only partial data. Use the datasample function and specify 'Replace','false' to sample data without replacement.

Bayesian Optimization with Tall Arrays

Get Data into MATLAB®

Prepare Class Labels and Predictor Data

Perform Bayesian Optimization Using OptimizeHyperparameters

Perform Bayesian Optimization by Using bayesopt

See Also

Perform Bayesian Optimization Using `OptimizeHyperparameters`

Perform Bayesian Optimization by Using `bayesopt`