fitckernel

Fit binary Gaussian kernel classifier using random feature expansion

collapse all in page

Syntax

Mdl = fitckernel(X,Y)

Mdl = fitckernel(Tbl,ResponseVarName)

Mdl = fitckernel(Tbl,formula)

Mdl = fitckernel(Tbl,Y)

Mdl = fitckernel(___,Name,Value)

[Mdl,FitInfo] = fitckernel(___)

[Mdl,FitInfo,HyperparameterOptimizationResults] = fitckernel(___)

[Mdl,AggregateOptimizationResults] = fitckernel(___)

Description

fitckernel trains or cross-validates a binary Gaussian kernel classification model for nonlinear classification. fitckernel is more practical for big data applications that have large training sets but can also be applied to smaller data sets that fit in memory.

fitckernel maps data in a low-dimensional space into a high-dimensional space, then fits a linear model in the high-dimensional space by minimizing the regularized objective function. Obtaining the linear model in the high-dimensional space is equivalent to applying the Gaussian kernel to the model in the low-dimensional space. Available linear classification models include regularized support vector machine (SVM) and logistic regression models.

To train a nonlinear SVM model for binary classification of in-memory data, see fitcsvm.

Mdl = fitckernel(X,Y) returns a binary Gaussian kernel classification model trained using the predictor data in X and the corresponding class labels in Y. The fitckernel function maps the predictors in a low-dimensional space into a high-dimensional space, then fits a binary SVM model to the transformed predictors and class labels. This linear model is equivalent to the Gaussian kernel classification model in the low-dimensional space.

example

Mdl = fitckernel(Tbl,ResponseVarName) returns a kernel classification model Mdl trained using the predictor variables contained in the table Tbl and the class labels in Tbl.ResponseVarName.

Mdl = fitckernel(Tbl,formula) returns a kernel classification model trained using the sample data in the table Tbl. The input argument formula is an explanatory model of the response and a subset of predictor variables in Tbl used to fit Mdl.

Mdl = fitckernel(Tbl,Y) returns a kernel classification model using the predictor variables in the table Tbl and the class labels in vector Y.

Mdl = fitckernel(___,Name,Value) specifies options using one or more name-value pair arguments in addition to any of the input argument combinations in previous syntaxes. For example, you can implement logistic regression, specify the number of dimensions of the expanded space, or specify to cross-validate.

example

[Mdl,FitInfo] = fitckernel(___) also returns the fit information in the structure array FitInfo using any of the input arguments in the previous syntaxes. You cannot request FitInfo for cross-validated models.

example

[Mdl,FitInfo,HyperparameterOptimizationResults] = fitckernel(___) also returns the hyperparameter optimization results when you specify OptimizeHyperparameters.

example

[Mdl,AggregateOptimizationResults] = fitckernel(___) also returns AggregateOptimizationResults, which contains hyperparameter optimization results when you specify the OptimizeHyperparameters and HyperparameterOptimizationOptions name-value arguments. You must also specify the ConstraintType and ConstraintBounds options of HyperparameterOptimizationOptions. You can use this syntax to optimize on compact model size instead of cross-validation loss, and to perform a set of multiple optimization problems that have the same options but different constraint bounds.

Examples

collapse all

Train Kernel Classification Model

Open Live Script

Train a binary kernel classification model using SVM.

Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, either bad ('b') or good ('g').

load ionosphere
[n,p] = size(X)

n = 
351

p = 
34

resp = unique(Y)

resp = 2x1 cell
    {'b'}
    {'g'}

Train a binary kernel classification model that identifies whether the radar return is bad ('b') or good ('g'). Extract a fit summary to determine how well the optimization algorithm fits the model to the data.

rng('default') % For reproducibility
[Mdl,FitInfo] = fitckernel(X,Y)

Mdl = 
  ClassificationKernel
              ResponseName: 'Y'
                ClassNames: {'b'  'g'}
                   Learner: 'svm'
    NumExpansionDimensions: 2048
               KernelScale: 1
                    Lambda: 0.0028
             BoxConstraint: 1

FitInfo = struct with fields:
                  Solver: 'LBFGS-fast'
            LossFunction: 'hinge'
                  Lambda: 0.0028
           BetaTolerance: 1.0000e-04
       GradientTolerance: 1.0000e-06
          ObjectiveValue: 0.2604
       GradientMagnitude: 0.0028
    RelativeChangeInBeta: 8.2512e-05
                 FitTime: 0.1059
                 History: []

Mdl is a ClassificationKernel model. To inspect the in-sample classification error, you can pass Mdl and the training data or new data to the loss function. Or, you can pass Mdl and new predictor data to the predict function to predict class labels for new observations. You can also pass Mdl and the training data to the resume function to continue training.

FitInfo is a structure array containing optimization information. Use FitInfo to determine whether optimization termination measurements are satisfactory.

For better accuracy, you can increase the maximum number of optimization iterations ('IterationLimit') and decrease the tolerance values ('BetaTolerance' and 'GradientTolerance') by using the name-value pair arguments. Doing so can improve measures like ObjectiveValue and RelativeChangeInBeta in FitInfo. You can also optimize model parameters by using the 'OptimizeHyperparameters' name-value pair argument.

Cross-Validate Kernel Classification Model

Open Live Script

Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, either bad ('b') or good ('g').

load ionosphere
rng('default') % For reproducibility

Cross-validate a binary kernel classification model. By default, the software uses 10-fold cross-validation.

CVMdl = fitckernel(X,Y,'CrossVal','on')

CVMdl = 
  ClassificationPartitionedKernel
    CrossValidatedModel: 'Kernel'
           ResponseName: 'Y'
        NumObservations: 351
                  KFold: 10
              Partition: [1x1 cvpartition]
             ClassNames: {'b'  'g'}
         ScoreTransform: 'none'

numel(CVMdl.Trained)

ans = 
10

CVMdl is a ClassificationPartitionedKernel model. Because fitckernel implements 10-fold cross-validation, CVMdl contains 10 ClassificationKernel models that the software trains on training-fold (in-fold) observations.

Estimate the cross-validated classification error.

kfoldLoss(CVMdl)

ans = 
0.0940

The classification error rate is approximately 9%.

Optimize Kernel Classifier

Open Live Script

Optimize hyperparameters automatically using the OptimizeHyperparameters name-value argument.

Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, either bad ('b') or good ('g').

load ionosphere

Find hyperparameters that minimize five-fold cross-validation loss by using automatic hyperparameter optimization. Specify OptimizeHyperparameters as 'auto' so that fitckernel finds optimal values of the KernelScale, Lambda, and Standardize name-value arguments. For reproducibility, set the random seed and use the 'expected-improvement-plus' acquisition function.

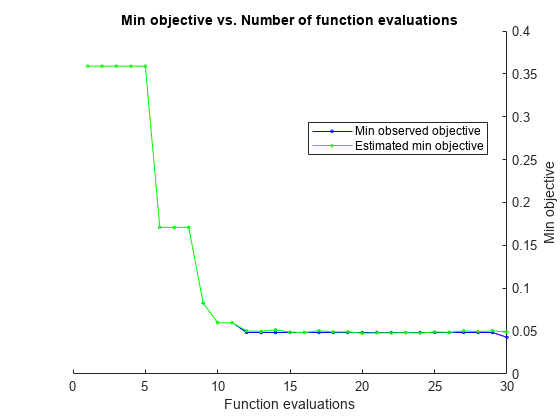
rng('default')
[Mdl,FitInfo,HyperparameterOptimizationResults] = fitckernel(X,Y,'OptimizeHyperparameters','auto',...
    'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName','expected-improvement-plus'))

|====================================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |  KernelScale |       Lambda |  Standardize |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |              |
|====================================================================================================================|
|    1 | Best   |     0.35897 |       2.242 |     0.35897 |     0.35897 |       3.8653 |       2.7394 |         true |
|    2 | Accept |     0.35897 |     0.40581 |     0.35897 |     0.35897 |       429.99 |    0.0006775 |        false |
|    3 | Accept |     0.35897 |     0.56457 |     0.35897 |     0.35897 |      0.11801 |     0.025493 |        false |
|    4 | Accept |     0.41311 |      0.5403 |     0.35897 |     0.35898 |    0.0010694 |   9.1346e-06 |         true |
|    5 | Accept |      0.4245 |     0.69443 |     0.35897 |     0.35898 |    0.0093918 |   2.8526e-06 |        false |
|    6 | Best   |     0.17094 |     0.36652 |     0.17094 |     0.17102 |       15.285 |    0.0038931 |        false |
|    7 | Accept |     0.18234 |     0.54203 |     0.17094 |     0.17099 |       9.9078 |    0.0090818 |        false |
|    8 | Accept |     0.35897 |     0.38998 |     0.17094 |     0.17097 |       26.961 |      0.46727 |        false |
|    9 | Best   |    0.082621 |     0.71096 |    0.082621 |    0.082677 |       7.7184 |    0.0025676 |        false |
|   10 | Best   |    0.059829 |     0.59853 |    0.059829 |    0.059839 |       5.6125 |    0.0013416 |        false |
|   11 | Accept |    0.062678 |     0.57988 |    0.059829 |    0.059793 |       7.3294 |   0.00062394 |        false |
|   12 | Best   |    0.048433 |      1.1187 |    0.048433 |    0.050198 |       3.7772 |   0.00032964 |        false |
|   13 | Accept |    0.051282 |      1.9346 |    0.048433 |    0.049662 |       3.4417 |   0.00077524 |        false |
|   14 | Accept |    0.054131 |      1.6788 |    0.048433 |    0.051494 |       4.3694 |   0.00055199 |        false |
|   15 | Accept |    0.051282 |      1.9217 |    0.048433 |     0.04872 |       1.7463 |   0.00012886 |        false |
|   16 | Accept |    0.048433 |      1.1643 |    0.048433 |    0.048475 |       3.9086 |   3.1147e-05 |        false |
|   17 | Accept |    0.054131 |      1.6661 |    0.048433 |    0.050325 |       3.1489 |   9.1315e-05 |        false |
|   18 | Accept |    0.051282 |     0.83412 |    0.048433 |    0.049131 |       2.3414 |   4.8238e-06 |        false |
|   19 | Accept |    0.062678 |      1.6912 |    0.048433 |    0.049062 |       7.2203 |   3.2694e-06 |        false |
|   20 | Accept |    0.054131 |     0.70691 |    0.048433 |    0.051225 |       3.5381 |   1.0341e-05 |        false |
|====================================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |  KernelScale |       Lambda |  Standardize |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |              |
|====================================================================================================================|
|   21 | Accept |    0.068376 |      0.6618 |    0.048433 |     0.05111 |       1.4267 |   1.7614e-05 |        false |
|   22 | Accept |    0.054131 |     0.89815 |    0.048433 |     0.05127 |       3.2173 |   2.9573e-06 |        false |
|   23 | Accept |     0.05698 |     0.97508 |    0.048433 |    0.051187 |       2.4241 |    0.0003272 |        false |
|   24 | Accept |    0.059829 |      1.2984 |    0.048433 |    0.051097 |       2.5948 |   4.5059e-05 |        false |
|   25 | Accept |    0.059829 |     0.88365 |    0.048433 |    0.051018 |       7.2989 |   2.6908e-05 |        false |
|   26 | Accept |    0.068376 |      1.2979 |    0.048433 |    0.048938 |       3.9585 |   6.9173e-06 |        false |
|   27 | Accept |     0.05698 |     0.99179 |    0.048433 |    0.051222 |       4.2751 |    0.0002231 |        false |
|   28 | Accept |    0.062678 |     0.54935 |    0.048433 |    0.051232 |       1.4533 |   2.8533e-06 |        false |
|   29 | Accept |    0.051282 |     0.91705 |    0.048433 |    0.051122 |       3.8449 |   0.00059747 |        false |
|   30 | Accept |     0.21083 |      1.2734 |    0.048433 |      0.0512 |       45.588 |    3.056e-06 |        false |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 45.5589 seconds
Total objective function evaluation time: 30.0979

Best observed feasible point:
    KernelScale      Lambda      Standardize
    ___________    __________    ___________

      3.7772       0.00032964       false   

Observed objective function value = 0.048433
Estimated objective function value = 0.05162
Function evaluation time = 1.1187

Best estimated feasible point (according to models):
    KernelScale      Lambda      Standardize
    ___________    __________    ___________

      3.8449       0.00059747       false   

Estimated objective function value = 0.0512
Estimated function evaluation time = 1.1518

Figure contains an axes object. The axes object with title Min objective vs. Number of function evaluations, xlabel Function evaluations, ylabel Min objective contains 2 objects of type line. These objects represent Min observed objective, Estimated min objective.

Mdl = 
  ClassificationKernel
              ResponseName: 'Y'
                ClassNames: {'b'  'g'}
                   Learner: 'svm'
    NumExpansionDimensions: 2048
               KernelScale: 3.8449
                    Lambda: 5.9747e-04
             BoxConstraint: 4.7684

FitInfo = struct with fields:
                  Solver: 'LBFGS-fast'
            LossFunction: 'hinge'
                  Lambda: 5.9747e-04
           BetaTolerance: 1.0000e-04
       GradientTolerance: 1.0000e-06
          ObjectiveValue: 0.1006
       GradientMagnitude: 0.0114
    RelativeChangeInBeta: 9.3027e-05
                 FitTime: 0.1670
                 History: []

HyperparameterOptimizationResults = 
  BayesianOptimization with properties:

                      ObjectiveFcn: @createObjFcn/inMemoryObjFcn
              VariableDescriptions: [5x1 optimizableVariable]
                           Options: [1x1 struct]
                      MinObjective: 0.0484
                   XAtMinObjective: [1x3 table]
             MinEstimatedObjective: 0.0512
          XAtMinEstimatedObjective: [1x3 table]
           NumObjectiveEvaluations: 30
                  TotalElapsedTime: 45.5589
                         NextPoint: [1x3 table]
                            XTrace: [30x3 table]
                    ObjectiveTrace: [30x1 double]
                  ConstraintsTrace: []
                     UserDataTrace: {30x1 cell}
      ObjectiveEvaluationTimeTrace: [30x1 double]
                IterationTimeTrace: [30x1 double]
                        ErrorTrace: [30x1 double]
                  FeasibilityTrace: [30x1 logical]
       FeasibilityProbabilityTrace: [30x1 double]
               IndexOfMinimumTrace: [30x1 double]
             ObjectiveMinimumTrace: [30x1 double]
    EstimatedObjectiveMinimumTrace: [30x1 double]

For big data, the optimization procedure can take a long time. If the data set is too large to run the optimization procedure, you can try to optimize the parameters using only partial data. Use the datasample function and specify 'Replace','false' to sample data without replacement.

Input Arguments

collapse all

`X` — Predictor data
numeric matrix

Predictor data, specified as an n-by-p numeric matrix, where n is the number of observations and p is the number of predictors.

The length of Y and the number of observations in X must be equal.

Data Types: single | double

`Y` — Class labels
categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

Class labels, specified as a categorical, character, or string array, logical or numeric vector, or cell array of character vectors.

fitckernel supports only binary classification. Either Y must contain exactly two distinct classes, or you must specify two classes for training by using the ClassNames name-value pair argument. For multiclass learning, see fitcecoc.
The length of Y must be equal to the number of observations in X or Tbl.
If Y is a character array, then each label must correspond to one row of the array.
A good practice is to specify the class order by using the ClassNames name-value pair argument.

`Tbl` — Sample data
table

Sample data used to train the model, specified as a table. Each row of Tbl corresponds to one observation, and each column corresponds to one predictor variable. Multicolumn variables and cell arrays other than cell arrays of character vectors are not allowed.

Optionally, Tbl can contain a column for the response variable and a column for the observation weights.

The response variable must be a categorical, character, or string array, a logical or numeric vector, or a cell array of character vectors.
- fitckernel supports only binary classification. Either the response variable must contain exactly two distinct classes, or you must specify two classes for training by using the ClassNames name-value argument. For multiclass learning, see fitcecoc.
- A good practice is to specify the order of the classes in the response variable by using the ClassNames name-value argument.
The column for the weights must be a numeric vector.
You must specify the response variable in Tbl by using ResponseVarName or formula and specify the observation weights in Tbl by using Weights.
- Specify the response variable by using ResponseVarName — fitckernel uses the remaining variables as predictors. To use a subset of the remaining variables in Tbl as predictors, specify predictor variables by using PredictorNames.
- Define a model specification by using formula — fitckernel uses a subset of the variables in Tbl as predictor variables and the response variable, as specified in formula.

If Tbl does not contain the response variable, then specify a response variable by using Y. The length of the response variable Y and the number of rows in Tbl must be equal. To use a subset of the variables in Tbl as predictors, specify predictor variables by using PredictorNames.

Data Types: table

`ResponseVarName` — Response variable name
name of variable in `Tbl`

Response variable name, specified as the name of a variable in Tbl.

You must specify ResponseVarName as a character vector or string scalar. For example, if the response variable Y is stored as Tbl.Y, then specify it as "Y". Otherwise, the software treats all columns of Tbl, including Y, as predictors when training the model.

The response variable must be a categorical, character, or string array; a logical or numeric vector; or a cell array of character vectors. If Y is a character array, then each element of the response variable must correspond to one row of the array.

A good practice is to specify the order of the classes by using the ClassNames name-value argument.

Data Types: char | string

`formula` — Explanatory model of response variable and subset of predictor variables
character vector | string scalar

Explanatory model of the response variable and a subset of the predictor variables, specified as a character vector or string scalar in the form "Y~x1+x2+x3". In this form, Y represents the response variable, and x1, x2, and x3 represent the predictor variables.

To specify a subset of variables in Tbl as predictors for training the model, use a formula. If you specify a formula, then the software does not use any variables in Tbl that do not appear in formula.

The variable names in the formula must be both variable names in Tbl (Tbl.Properties.VariableNames) and valid MATLAB^® identifiers. You can verify the variable names in Tbl by using the isvarname function. If the variable names are not valid, then you can convert them by using the matlab.lang.makeValidName function.

Data Types: char | string

Note

The software treats NaN, empty character vector (''), empty string (""), <missing>, and <undefined> elements as missing values, and removes observations with any of these characteristics:

Missing value in the response variable
At least one missing value in a predictor observation (row in X or Tbl)
NaN value or 0 weight ('Weights')

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: Mdl = fitckernel(X,Y,'Learner','logistic','NumExpansionDimensions',2^15,'KernelScale','auto') implements logistic regression after mapping the predictor data to the 2^15 dimensional space using feature expansion with a kernel scale parameter selected by a heuristic procedure.

Note

You cannot use any cross-validation name-value argument together with the OptimizeHyperparameters name-value argument. You can modify the cross-validation for OptimizeHyperparameters only by using the HyperparameterOptimizationOptions name-value argument.

Kernel Classification Options

collapse all

`Learner` — Linear classification model type
`'svm'` (default) | `'logistic'`

Linear classification model type, specified as the comma-separated pair consisting of 'Learner' and 'svm' or 'logistic'.

In the following table, $f (x) = T (x) β + b .$

x is an observation (row vector) from p predictor variables.
$T (\cdot)$ is a transformation of an observation (row vector) for feature expansion. T(x) maps x in $ℝ^{p}$ to a high-dimensional space ( $ℝ^{m}$ ).
β is a vector of coefficients.
b is the scalar bias.

Value	Algorithm	Response Range	Loss Function
`'svm'`	Support vector machine	y ∊ {–1,1}; 1 for the positive class and –1 otherwise	Hinge: $ℓ [y, f (x)] = \max [0, 1 - y f (x)]$
`'logistic'`	Logistic regression	Same as `'svm'`	Deviance (logistic): $ℓ [y, f (x)] = \log {1 + \exp [- y f (x)]}$

Example: 'Learner','logistic'

`NumExpansionDimensions` — Number of dimensions of expanded space
`'auto'` (default) | positive integer

Number of dimensions of the expanded space, specified as the comma-separated pair consisting of 'NumExpansionDimensions' and 'auto' or a positive integer. For 'auto', the fitckernel function selects the number of dimensions using 2.^ceil(min(log2(p)+5,15)), where p is the number of predictors.

For details, see Random Feature Expansion.

Example: 'NumExpansionDimensions',2^15

Data Types: char | string | single | double

`KernelScale` — Kernel scale parameter
`1` (default) | `"auto"` | positive scalar

Kernel scale parameter, specified as "auto" or a positive scalar. The software obtains a random basis for random feature expansion by using the kernel scale parameter. For details, see Random Feature Expansion.

If you specify "auto", then the software selects an appropriate kernel scale parameter using a heuristic procedure. This heuristic procedure uses subsampling, so estimates can vary from one call to another. Therefore, to reproduce results, set a random number seed by using rng before training.

Example: KernelScale="auto"

Data Types: char | string | single | double

`BoxConstraint` — Box constraint
1 (default) | positive scalar

Box constraint, specified as the comma-separated pair consisting of 'BoxConstraint' and a positive scalar.

This argument is valid only when 'Learner' is 'svm'(default) and you do not specify a value for the regularization term strength 'Lambda'. You can specify either 'BoxConstraint' or 'Lambda' because the box constraint (C) and the regularization term strength (λ) are related by C = 1/(λn), where n is the number of observations.

Example: 'BoxConstraint',100

Data Types: single | double

`Lambda` — Regularization term strength
`'auto'` (default) | nonnegative scalar

Regularization term strength, specified as the comma-separated pair consisting of 'Lambda' and 'auto' or a nonnegative scalar.

For 'auto', the value of Lambda is 1/n, where n is the number of observations.

When Learner is 'svm', you can specify either BoxConstraint or Lambda because the box constraint (C) and the regularization term strength (λ) are related by C = 1/(λn).

Example: 'Lambda',0.01

Data Types: char | string | single | double

`Standardize` — Flag to standardize predictor data
`false` or `0` (default) | `true` or `1`

Since R2023b

Flag to standardize the predictor data, specified as a numeric or logical 0 (false) or 1 (true). If you set Standardize to true, then the software centers and scales each numeric predictor variable by the corresponding column mean and standard deviation. The software does not standardize the categorical predictors.

Example: "Standardize",true

Data Types: single | double | logical

Cross-Validation Options

collapse all

`CrossVal` — Flag to train cross-validated classifier
`'off'` (default) | `'on'`

Flag to train a cross-validated classifier, specified as the comma-separated pair consisting of 'Crossval' and 'on' or 'off'.

If you specify 'on', then the software trains a cross-validated classifier with 10 folds.

You can override this cross-validation setting using the CVPartition, Holdout, KFold, or Leaveout name-value pair argument. You can use only one cross-validation name-value pair argument at a time to create a cross-validated model.

Example: 'Crossval','on'

`CVPartition` — Cross-validation partition
`[]` (default) | `cvpartition` object

Cross-validation partition, specified as a cvpartition object that specifies the type of cross-validation and the indexing for the training and validation sets.

To create a cross-validated model, you can specify only one of these four name-value arguments: CVPartition, Holdout, KFold, or Leaveout.

Example: Suppose you create a random partition for 5-fold cross-validation on 500 observations by using cvp = cvpartition(500,KFold=5). Then, you can specify the cross-validation partition by setting CVPartition=cvp.

`Holdout` — Fraction of data for holdout validation
scalar value in the range (0,1)

Fraction of the data used for holdout validation, specified as a scalar value in the range (0,1). If you specify Holdout=p, then the software completes these steps:

Randomly select and reserve p*100% of the data as validation data, and train the model using the rest of the data.
Store the compact trained model in the Trained property of the cross-validated model.

To create a cross-validated model, you can specify only one of these four name-value arguments: CVPartition, Holdout, KFold, or Leaveout.

Example: Holdout=0.1

Data Types: double | single

`KFold` — Number of folds
`10` (default) | positive integer value greater than 1

Number of folds to use in the cross-validated model, specified as a positive integer value greater than 1. If you specify KFold=k, then the software completes these steps:

Randomly partition the data into k sets.
For each set, reserve the set as validation data, and train the model using the other k – 1 sets.
Store the k compact trained models in a k-by-1 cell vector in the Trained property of the cross-validated model.

To create a cross-validated model, you can specify only one of these four name-value arguments: CVPartition, Holdout, KFold, or Leaveout.

Example: KFold=5

Data Types: single | double

`Leaveout` — Leave-one-out cross-validation flag
`'off'` (default) | `'on'`

Leave-one-out cross-validation flag, specified as the comma-separated pair consisting of 'Leaveout' and 'on' or 'off'. If you specify 'Leaveout','on', then, for each of the n observations (where n is the number of observations excluding missing observations), the software completes these steps:

Reserve the observation as validation data, and train the model using the other n – 1 observations.
Store the n compact, trained models in the cells of an n-by-1 cell vector in the Trained property of the cross-validated model.

To create a cross-validated model, you can use one of these four name-value pair arguments only: CVPartition, Holdout, KFold, or Leaveout.

Example: 'Leaveout','on'

Convergence Controls

collapse all

`BetaTolerance` — Relative tolerance on linear coefficients and bias term
`1e–4` (default) | nonnegative scalar

Relative tolerance on the linear coefficients and the bias term (intercept), specified as a nonnegative scalar.

Let $B_{t} = [β_{t}^{'} b_{t}]$ , that is, the vector of the coefficients and the bias term at optimization iteration t. If ${‖ \frac{B_{t} - B_{t - 1}}{B_{t}} ‖}_{2} < BetaTolerance$ , then optimization terminates.

If you also specify GradientTolerance, then optimization terminates when the software satisfies either stopping criterion.

Example: BetaTolerance=1e–6

Data Types: single | double

`GradientTolerance` — Absolute gradient tolerance
`1e–6` (default) | nonnegative scalar

Absolute gradient tolerance, specified as a nonnegative scalar.

Let $\nabla ℒ_{t}$ be the gradient vector of the objective function with respect to the coefficients and bias term at optimization iteration t. If ${‖ \nabla ℒ_{t} ‖}_{\infty} = \max | \nabla ℒ_{t} | < GradientTolerance$ , then optimization terminates.

If you also specify BetaTolerance, then optimization terminates when the software satisfies either stopping criterion.

Example: GradientTolerance=1e–5

Data Types: single | double

`IterationLimit` — Maximum number of optimization iterations
positive integer

Maximum number of optimization iterations, specified as a positive integer.

The default value is 1000 if the transformed data fits in memory, as specified by the BlockSize name-value argument. Otherwise, the default value is 100.

Example: IterationLimit=500

Data Types: single | double

Other Kernel Classification Options

collapse all

`BlockSize` — Maximum amount of allocated memory
`4e^3` (4GB) (default) | positive scalar

Maximum amount of allocated memory (in megabytes), specified as the comma-separated pair consisting of 'BlockSize' and a positive scalar.

If fitckernel requires more memory than the value of 'BlockSize' to hold the transformed predictor data, then the software uses a block-wise strategy. For details about the block-wise strategy, see Algorithms.

Example: 'BlockSize',1e4

Data Types: single | double

`RandomStream` — Random number stream
global stream (default) | random stream object

Random number stream for reproducibility of data transformation, specified as a random stream object. For details, see Random Feature Expansion.

Use RandomStream to reproduce the random basis functions used by fitckernel to transform the predictor data to a high-dimensional space. For details, see Managing the Global Stream Using RandStream and Creating and Controlling a Random Number Stream.

Example: RandomStream=RandStream("mlfg6331_64")

`HessianHistorySize` — Size of history buffer for Hessian approximation
`15` (default) | positive integer

Size of the history buffer for Hessian approximation, specified as the comma-separated pair consisting of 'HessianHistorySize' and a positive integer. At each iteration, fitckernel composes the Hessian approximation by using statistics from the latest HessianHistorySize iterations.

Example: 'HessianHistorySize',10

Data Types: single | double

`Verbose` — Verbosity level
`0` (default) | `1`

Verbosity level, specified as the comma-separated pair consisting of 'Verbose' and either 0 or 1. Verbose controls the display of diagnostic information at the command line.

Value	Description
`0`	`fitckernel` does not display diagnostic information.
`1`	`fitckernel` displays and stores the value of the objective function, gradient magnitude, and other diagnostic information. `FitInfo.History` contains the diagnostic information.

Example: 'Verbose',1

Data Types: single | double

Other Classification Options

collapse all

`CategoricalPredictors` — Categorical predictors list
vector of positive integers | logical vector | character matrix | string array | cell array of character vectors | `'all'`

Categorical predictors list, specified as one of the values in this table.

Value	Description
Vector of positive integers	Each entry in the vector is an index value indicating that the corresponding predictor is categorical. The index values are between 1 and `p`, where `p` is the number of predictors used to train the model. If `fitckernel` uses a subset of input variables as predictors, then the function indexes the predictors using only the subset. The `CategoricalPredictors` values do not count any response variable, observation weights variable, or other variable that the function does not use.
Logical vector	A `true` entry means that the corresponding predictor is categorical. The length of the vector is `p`.
Character matrix	Each row of the matrix is the name of a predictor variable. The names must match the entries in `PredictorNames`. Pad the names with extra blanks so each row of the character matrix has the same length.
String array or cell array of character vectors	Each element in the array is the name of a predictor variable. The names must match the entries in `PredictorNames`.
`"all"`	All predictors are categorical.

By default, if the predictor data is in a table (Tbl), fitckernel assumes that a variable is categorical if it is a logical vector, categorical vector, character array, string array, or cell array of character vectors. If the predictor data is a matrix (X), fitckernel assumes that all predictors are continuous. To identify any other predictors as categorical predictors, specify them by using the CategoricalPredictors name-value argument.

For the identified categorical predictors, fitckernel creates dummy variables using two different schemes, depending on whether a categorical variable is unordered or ordered. For an unordered categorical variable, fitckernel creates one dummy variable for each level of the categorical variable. For an ordered categorical variable, fitckernel creates one less dummy variable than the number of categories. For details, see Automatic Creation of Dummy Variables.

Example: 'CategoricalPredictors','all'

`ClassNames` — Names of classes to use for training
categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

Names of classes to use for training, specified as a categorical, character, or string array; a logical or numeric vector; or a cell array of character vectors. ClassNames must have the same data type as the response variable in Tbl or Y.

If ClassNames is a character array, then each element must correspond to one row of the array.

Use ClassNames to:

Specify the order of the classes during training.
Specify the order of any input or output argument dimension that corresponds to the class order. For example, use ClassNames to specify the order of the dimensions of Cost or the column order of classification scores returned by predict.
Select a subset of classes for training. For example, suppose that the set of all distinct class names in Y is ["a","b","c"]. To train the model using observations from classes "a" and "c" only, specify "ClassNames",["a","c"].

The default value for ClassNames is the set of all distinct class names in the response variable in Tbl or Y.

Example: "ClassNames",["b","g"]

`Cost` — Misclassification cost
square matrix | structure array

Misclassification cost, specified as the comma-separated pair consisting of 'Cost' and a square matrix or structure.

If you specify the square matrix cost ('Cost',cost), then cost(i,j) is the cost of classifying a point into class j if its true class is i. That is, the rows correspond to the true class, and the columns correspond to the predicted class. To specify the class order for the corresponding rows and columns of cost, use the ClassNames name-value pair argument.
If you specify the structure S ('Cost',S), then it must have two fields:
- S.ClassNames, which contains the class names as a variable of the same data type as Y
- S.ClassificationCosts, which contains the cost matrix with rows and columns ordered as in S.ClassNames

The default value for Cost is ones(K) – eye(K), where K is the number of distinct classes.

fitckernel uses Cost to adjust the prior class probabilities specified in Prior. Then, fitckernel uses the adjusted prior probabilities for training.

Example: 'Cost',[0 2; 1 0]

Data Types: single | double | struct

`PredictorNames` — Predictor variable names
string array of unique names | cell array of unique character vectors

Predictor variable names, specified as a string array of unique names or cell array of unique character vectors. The functionality of PredictorNames depends on the way you supply the training data.

If you supply X and Y, then you can use PredictorNames to assign names to the predictor variables in X.
- The order of the names in PredictorNames must correspond to the column order of X. That is, PredictorNames{1} is the name of X(:,1), PredictorNames{2} is the name of X(:,2), and so on. Also, size(X,2) and numel(PredictorNames) must be equal.
- By default, PredictorNames is {'x1','x2',...}.
If you supply Tbl, then you can use PredictorNames to choose which predictor variables to use in training. That is, fitckernel uses only the predictor variables in PredictorNames and the response variable during training.
- PredictorNames must be a subset of Tbl.Properties.VariableNames and cannot include the name of the response variable.
- By default, PredictorNames contains the names of all predictor variables.
- A good practice is to specify the predictors for training using either PredictorNames or formula, but not both.

Example: "PredictorNames",["SepalLength","SepalWidth","PetalLength","PetalWidth"]

Data Types: string | cell

`Prior` — Prior probabilities
`'empirical'` (default) | `'uniform'` | numeric vector | structure array

Prior probabilities for each class, specified as the comma-separated pair consisting of 'Prior' and 'empirical', 'uniform', a numeric vector, or a structure array.

This table summarizes the available options for setting prior probabilities.

Value	Description
`'empirical'`	The class prior probabilities are the class relative frequencies in `Y`.
`'uniform'`	All class prior probabilities are equal to 1/`K`, where `K` is the number of classes.
numeric vector	Each element is a class prior probability. Order the elements according to their order in `Y`. If you specify the order using the `'ClassNames'` name-value pair argument, then order the elements accordingly.
structure array	A structure `S` with two fields: `S.ClassNames` contains the class names as a variable of the same type as `Y`. `S.ClassProbs` contains a vector of corresponding prior probabilities.

fitckernel normalizes the prior probabilities in Prior to sum to 1.

Example: 'Prior',struct('ClassNames',{{'setosa','versicolor'}},'ClassProbs',1:2)

Data Types: char | string | double | single | struct

`ResponseName` — Response variable name
`"Y"` (default) | character vector | string scalar

Response variable name, specified as a character vector or string scalar.

If you supply Y, then you can use ResponseName to specify a name for the response variable.
If you supply ResponseVarName or formula, then you cannot use ResponseName.

Example: ResponseName="response"

Data Types: char | string

`ScoreTransform` — Score transformation
`"none"` (default) | `"doublelogit"` | `"invlogit"` | `"ismax"` | `"logit"` | function handle | ...

Score transformation, specified as a character vector, string scalar, or function handle.

This table summarizes the available character vectors and string scalars.

Value	Description
`"doublelogit"`	1/(1 + e^–2x)
`"invlogit"`	log(x / (1 – x))
`"ismax"`	Sets the score for the class with the largest score to 1, and sets the scores for all other classes to 0
`"logit"`	1/(1 + e^–x)
`"none"` or `"identity"`	x (no transformation)
`"sign"`	–1 for x < 0 0 for x = 0 1 for x > 0
`"symmetric"`	2x – 1
`"symmetricismax"`	Sets the score for the class with the largest score to 1, and sets the scores for all other classes to –1
`"symmetriclogit"`	2/(1 + e^–x) – 1

For a MATLAB function or a function you define, use its function handle for the score transform. The function handle must accept a matrix (the original scores) and return a matrix of the same size (the transformed scores).

Example: "ScoreTransform","logit"

Data Types: char | string | function_handle

`Weights` — Observation weights
nonnegative numeric vector | name of variable in `Tbl`

Observation weights, specified as a nonnegative numeric vector or the name of a variable in Tbl. The software weights each observation in X or Tbl with the corresponding value in Weights. The length of Weights must equal the number of observations in X or Tbl.

If you specify the input data as a table Tbl, then Weights can be the name of a variable in Tbl that contains a numeric vector. In this case, you must specify Weights as a character vector or string scalar. For example, if the weights vector W is stored as Tbl.W, then specify it as 'W'. Otherwise, the software treats all columns of Tbl, including W, as predictors or the response variable when training the model.

By default, Weights is ones(n,1), where n is the number of observations in X or Tbl.

The software normalizes Weights to sum to the value of the prior probability in the respective class.

Data Types: single | double | char | string

Hyperparameter Optimization Options

collapse all

`OptimizeHyperparameters` — Parameters to optimize
`'none'` (default) | `'auto'` | `'all'` | string array or cell array of eligible parameter names | vector of `optimizableVariable` objects

Parameters to optimize, specified as the comma-separated pair consisting of 'OptimizeHyperparameters' and one of these values:

'none' — Do not optimize.
'auto' — Use {'KernelScale','Lambda','Standardize'}.
'all' — Optimize all eligible parameters.
Cell array of eligible parameter names.
Vector of optimizableVariable objects, typically the output of hyperparameters.

The optimization attempts to minimize the cross-validation loss (error) for fitckernel by varying the parameters. To control the cross-validation type and other aspects of the optimization, use the HyperparameterOptimizationOptions name-value argument. When you use HyperparameterOptimizationOptions, you can use the (compact) model size instead of the cross-validation loss as the optimization objective by setting the ConstraintType and ConstraintBounds options.

Note

The values of OptimizeHyperparameters override any values you specify using other name-value arguments. For example, setting OptimizeHyperparameters to "auto" causes fitckernel to optimize hyperparameters corresponding to the "auto" option and to ignore any specified values for the hyperparameters.

The eligible parameters for fitckernel are:

KernelScale — fitckernel searches among positive values, by default log-scaled in the range [1e-3,1e3].
Lambda — fitckernel searches among positive values, by default log-scaled in the range [1e-3,1e3]/n, where n is the number of observations.
Learner — fitckernel searches among 'svm' and 'logistic'.
NumExpansionDimensions — fitckernel searches among positive integers, by default log-scaled in the range [100,10000].
Standardize — fitckernel searches among true and false.

Set nondefault parameters by passing a vector of optimizableVariable objects that have nondefault values. For example:

load fisheriris
params = hyperparameters('fitckernel',meas,species);
params(2).Range = [1e-4,1e6];

Pass params as the value of 'OptimizeHyperparameters'.

By default, the iterative display appears at the command line, and plots appear according to the number of hyperparameters in the optimization. For the optimization and plots, the objective function is the misclassification rate. To control the iterative display, set the Verbose option of the HyperparameterOptimizationOptions name-value argument. To control the plots, set the ShowPlots field of the HyperparameterOptimizationOptions name-value argument.

For an example, see Optimize Kernel Classifier.

Example: 'OptimizeHyperparameters','auto'

`HyperparameterOptimizationOptions` — Options for optimization
`HyperparameterOptimizationOptions` object | structure

Options for optimization, specified as a HyperparameterOptimizationOptions object or a structure. This argument modifies the effect of the OptimizeHyperparameters name-value argument. If you specify HyperparameterOptimizationOptions, you must also specify OptimizeHyperparameters. All the options are optional. However, you must set ConstraintBounds and ConstraintType to return AggregateOptimizationResults. The options that you can set in a structure are the same as those in the HyperparameterOptimizationOptions object.

Option	Values	Default
`Optimizer`	`"bayesopt"` — Use Bayesian optimization. Internally, this setting calls `bayesopt`. `"gridsearch"` — Use grid search with `NumGridDivisions` values per dimension. `"gridsearch"` searches in a random order, using uniform sampling without replacement from the grid. After optimization, you can get a table in grid order by using the command `sortrows(Mdl.HyperparameterOptimizationResults)`. `"randomsearch"` — Search at random among `MaxObjectiveEvaluations` points.	`"bayesopt"`
`ConstraintBounds`	Constraint bounds for N optimization problems, specified as an N-by-2 numeric matrix or `[]`. The columns of `ConstraintBounds` contain the lower and upper bound values of the optimization problems. If you specify `ConstraintBounds` as a numeric vector, the software assigns the values to the second column of `ConstraintBounds`, and zeros to the first column. If you specify `ConstraintBounds`, you must also specify `ConstraintType`.	`[]`
`ConstraintTarget`	Constraint target for the optimization problems, specified as `"matlab"` or `"coder"`. If `ConstraintBounds` and `ConstraintType` are `[]` and you set `ConstraintTarget`, then the software sets `ConstraintTarget` to `[]`. The values of `ConstraintTarget` and `ConstraintType` determine the objective and constraint functions. For more information, see `HyperparameterOptimizationOptions`.	If you specify `ConstraintBounds` and `ConstraintType`, then the default value is `"matlab"`. Otherwise, the default value is `[]`.
`ConstraintType`	Constraint type for the optimization problems, specified as `"size"` or `"loss"`. If you specify `ConstraintType`, you must also specify `ConstraintBounds`. The values of `ConstraintTarget` and `ConstraintType` determine the objective and constraint functions. For more information, see `HyperparameterOptimizationOptions`.	`[]`
`AcquisitionFunctionName`	Type of acquisition function: `"expected-improvement-per-second-plus"` `"expected-improvement"` `"expected-improvement-plus"` `"expected-improvement-per-second"` `"lower-confidence-bound"` `"probability-of-improvement"` Acquisition functions whose names include `per-second` do not yield reproducible results, because the optimization depends on the run time of the objective function. Acquisition functions whose names include `plus` modify their behavior when they overexploit an area. For more details, see Acquisition Function Types.	`"expected-improvement-per-second-plus"`
`MaxObjectiveEvaluations`	Maximum number of objective function evaluations. If you specify multiple optimization problems using `ConstraintBounds`, the value of `MaxObjectiveEvaluations` applies to each optimization problem individually.	`30` for `"bayesopt"` and `"randomsearch"`, and the entire grid for `"gridsearch"`
`MaxTime`	Time limit for the optimization, specified as a nonnegative real scalar. The time limit is in seconds, as measured by `tic` and `toc`. The software performs at least one optimization iteration, regardless of the value of `MaxTime`. The run time can exceed `MaxTime` because `MaxTime` does not interrupt function evaluations. If you specify multiple optimization problems using `ConstraintBounds`, the time limit applies to each optimization problem individually.	`Inf`
`NumGridDivisions`	For `Optimizer="gridsearch"`, the number of values in each dimension. The value can be a vector of positive integers giving the number of values for each dimension, or a scalar that applies to all dimensions. This option is ignored for categorical variables.	`10`
`ShowPlots`	Logical value indicating whether to show plots of the optimization progress. If this option is `true`, the software plots the best observed objective function value against the iteration number. If you use Bayesian optimization (`Optimizer="bayesopt"`), then the software also plots the best estimated objective function value. The best observed objective function values and best estimated objective function values correspond to the values in the `BestSoFar (observed)` and `BestSoFar (estim.)` columns of the iterative display, respectively. You can find these values in the properties `ObjectiveMinimumTrace` and `EstimatedObjectiveMinimumTrace` of `Mdl.HyperparameterOptimizationResults`. If the problem includes one or two optimization parameters for Bayesian optimization, then `ShowPlots` also plots a model of the objective function against the parameters.	`true`
`SaveIntermediateResults`	Logical value indicating whether to save the optimization results. If this option is `true`, the software overwrites a workspace variable named `"BayesoptResults"` at each iteration. The variable is a `BayesianOptimization` object. If you specify multiple optimization problems using `ConstraintBounds`, the workspace variable is an `AggregateBayesianOptimization` object named `"AggregateBayesoptResults"`.	`false`
`Verbose`	Display level at the command line: `0` — No iterative display `1` — Iterative display `2` — Iterative display with additional information For details, see the `bayesopt` `Verbose` name-value argument and the example Optimize Classifier Fit Using Bayesian Optimization.	`1`
`UseParallel`	Logical value indicating whether to run the Bayesian optimization in parallel, which requires Parallel Computing Toolbox™. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results. For details, see Parallel Bayesian Optimization.	`false`
`Repartition`	Logical value indicating whether to repartition the cross-validation at every iteration. If this option is `false`, the optimizer uses a single partition for the optimization. A value of `true` usually gives the most robust results because this setting takes partitioning noise into account. However, for optimal results, `true` requires at least twice as many function evaluations.	`false`
Specify only one of the following three options.
`CVPartition`	`cvpartition` object created by `cvpartition`	`Kfold=5` if you do not specify a cross-validation option
`Holdout`	Scalar in the range `(0,1)` representing the holdout fraction
`Kfold`	Integer greater than 1

Example: HyperparameterOptimizationOptions=struct(UseParallel=true)

Output Arguments

collapse all

`Mdl` — Trained kernel classification model
`ClassificationKernel` model object | `ClassificationPartitionedKernel` cross-validated model object

Trained kernel classification model, returned as a ClassificationKernel model object or ClassificationPartitionedKernel cross-validated model object.

If you set any of the name-value pair arguments CrossVal, CVPartition, Holdout, KFold, or Leaveout, then Mdl is a ClassificationPartitionedKernel cross-validated classifier. Otherwise, Mdl is a ClassificationKernel classifier.

To reference properties of Mdl, use dot notation. For example, enter Mdl.NumExpansionDimensions in the Command Window to display the number of dimensions of the expanded space.

If you specify OptimizeHyperparameters and set the ConstraintType and ConstraintBounds options of HyperparameterOptimizationOptions, then Mdl is an N-by-1 cell array of model objects, where N is equal to the number of rows in ConstraintBounds. If none of the optimization problems yields a feasible model, then each cell array value is [].

Note

Unlike other classification models, and for economical memory usage, a ClassificationKernel model object does not store the training data or training process details (for example, convergence history).

`AggregateOptimizationResults` — Aggregate optimization results
`AggregateBayesianOptimization` object

Aggregate optimization results for multiple optimization problems, returned as an AggregateBayesianOptimization object. To return AggregateOptimizationResults, you must specify OptimizeHyperparameters and HyperparameterOptimizationOptions. You must also specify the ConstraintType and ConstraintBounds options of HyperparameterOptimizationOptions. For an example that shows how to produce this output, see Hyperparameter Optimization with Multiple Constraint Bounds.

`FitInfo` — Optimization details
structure array

Optimization details, returned as a structure array including fields described in this table. The fields contain final values or name-value pair argument specifications.

Field	Description
`Solver`	Objective function minimization technique: `'LBFGS-fast'`, `'LBFGS-blockwise'`, or `'LBFGS-tall'`. For details, see Algorithms.
`LossFunction`	Loss function. Either `'hinge'` or `'logit'` depending on the type of linear classification model. See `Learner`.
`Lambda`	Regularization term strength. See `Lambda`.
`BetaTolerance`	Relative tolerance on the linear coefficients and the bias term. See `BetaTolerance`.
`GradientTolerance`	Absolute gradient tolerance. See `GradientTolerance`.
`ObjectiveValue`	Value of the objective function when optimization terminates. The classification loss plus the regularization term compose the objective function.
`GradientMagnitude`	Infinite norm of the gradient vector of the objective function when optimization terminates. See `GradientTolerance`.
`RelativeChangeInBeta`	Relative changes in the linear coefficients and the bias term when optimization terminates. See `BetaTolerance`.
`FitTime`	Elapsed, wall-clock time (in seconds) required to fit the model to the data.
`History`	History of optimization information. This field is empty (`[]`) if you specify `'Verbose',0`. For details, see `Verbose` and Algorithms.

To access fields, use dot notation. For example, to access the vector of objective function values for each iteration, enter FitInfo.ObjectiveValue in the Command Window.

If you specify OptimizeHyperparameters and set the ConstraintType and ConstraintBounds options of HyperparameterOptimizationOptions, then Fitinfo is an N-by-1 cell array of structure arrays, where N is equal to the number of rows in ConstraintBounds.

A good practice is to examine FitInfo to assess whether convergence is satisfactory.

`HyperparameterOptimizationResults` — Cross-validation optimization of hyperparameters
`BayesianOptimization` object | `AggregateBayesianOptimization` object | table of hyperparameters and associated values

Cross-validation optimization of hyperparameters, returned as a BayesianOptimization object, an AggregateBayesianOptimization object, or a table of hyperparameters and associated values. The output is nonempty when OptimizeHyperparameters has a value other than "none".

If you set the ConstraintType and ConstraintBounds options in HyperparameterOptimizationOptions, then HyperparameterOptimizationResults is an AggregateBayesianOptimization object. Otherwise, the value of HyperparameterOptimizationResults depends on the value of the Optimizer option in HyperparameterOptimizationOptions.

Value of `Optimizer` Option	Value of `HyperparameterOptimizationResults`
`"bayesopt"` (default)	Object of class `BayesianOptimization`
`"gridsearch"` or `"randomsearch"`	Table of hyperparameters used, observed objective function values (cross-validation loss), and rank of observations from lowest (best) to highest (worst)

More About

collapse all

Random Feature Expansion

Random feature expansion, such as Random Kitchen Sinks [1] or Fastfood [2], is a scheme to approximate Gaussian kernels of the kernel classification algorithm to use for big data in a computationally efficient way. Random feature expansion is more practical for big data applications that have large training sets, but can also be applied to smaller data sets that fit in memory.

The kernel classification algorithm searches for an optimal hyperplane that separates the data into two classes after mapping features into a high-dimensional space. Nonlinear features that are not linearly separable in a low-dimensional space can be separable in the expanded high-dimensional space. All the calculations for hyperplane classification use only dot products. You can obtain a nonlinear classification model by replacing the dot product x₁x₂' with the nonlinear kernel function $G (x_{1}, x_{2}) = 〈 φ (x_{1}), φ (x_{2}) 〉$ , where x_i is the ith observation (row vector) and φ(x_i) is a transformation that maps x_i to a high-dimensional space (called the “kernel trick”). However, evaluating G(x₁,x₂) (Gram matrix) for each pair of observations is computationally expensive for a large data set (large n).

The random feature expansion scheme finds a random transformation so that its dot product approximates the Gaussian kernel. That is,

$G (x_{1}, x_{2}) = 〈 φ (x_{1}), φ (x_{2}) 〉 \approx T (x_{1}) T (x_{2})',$

where T(x) maps x in $ℝ^{p}$ to a high-dimensional space ( $ℝ^{m}$ ). The Random Kitchen Sinks scheme uses the random transformation

$T (x) = m^{- 1 / 2} \exp (i Z x')',$

where $Z \in ℝ^{m \times p}$ is a sample drawn from $N (0, σ^{- 2})$ and σ is a kernel scale. This scheme requires O(mp) computation and storage.

The Fastfood scheme introduces another random basis V instead of Z using Hadamard matrices combined with Gaussian scaling matrices. This random basis reduces the computation cost to O(mlogp) and reduces storage to O(m).

You can specify values for m and σ by setting NumExpansionDimensions and KernelScale, respectively, of fitckernel.

The fitckernel function uses the Fastfood scheme for random feature expansion and uses linear classification to train a Gaussian kernel classification model. Unlike solvers in the fitcsvm function, which require computation of the n-by-n Gram matrix, the solver in fitckernel only needs to form a matrix of size n-by-m, with m typically much less than n for big data.

Box Constraint

A box constraint is a parameter that controls the maximum penalty imposed on margin-violating observations, and aids in preventing overfitting (regularization). Increasing the box constraint can lead to longer training times.

The box constraint (C) and the regularization term strength (λ) are related by C = 1/(λn), where n is the number of observations.

Tips

Standardizing predictors before training a model can be helpful.
- You can standardize training data and scale test data to have the same scale as the training data by using the normalize function.
- Alternatively, use the Standardize name-value argument to standardize the numeric predictors before training. The returned model includes the predictor means and standard deviations in its Mu and Sigma properties, respectively. (since R2023b)
After training a model, you can generate C/C++ code that predicts labels for new data. Generating C/C++ code requires MATLAB Coder™. For details, see Introduction to Code Generation.

Algorithms

fitckernel minimizes the regularized objective function using a Limited-memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) solver with ridge (L₂) regularization. To find the type of LBFGS solver used for training, type FitInfo.Solver in the Command Window.
- 'LBFGS-fast' — LBFGS solver.
- 'LBFGS-blockwise' — LBFGS solver with a block-wise strategy. If fitckernel requires more memory than the value of BlockSize to hold the transformed predictor data, then the function uses a block-wise strategy.
- 'LBFGS-tall' — LBFGS solver with a block-wise strategy for tall arrays.
When fitckernel uses a block-wise strategy, it implements LBFGS by distributing the calculation of the loss and gradient among different parts of the data at each iteration. Also, fitckernel refines the initial estimates of the linear coefficients and the bias term by fitting the model locally to parts of the data and combining the coefficients by averaging. If you specify 'Verbose',1, then fitckernel displays diagnostic information for each data pass and stores the information in the History field of FitInfo.
When fitckernel does not use a block-wise strategy, the initial estimates are zeros. If you specify 'Verbose',1, then fitckernel displays diagnostic information for each iteration and stores the information in the History field of FitInfo.
If you specify the Cost, Prior, and Weights name-value arguments, the output model object stores the specified values in the Cost, Prior, and W properties, respectively. The Cost property stores the user-specified cost matrix (C) without modification. The Prior and W properties store the prior probabilities and observation weights, respectively, after normalization. For model training, the software updates the prior probabilities and observation weights to incorporate the penalties described in the cost matrix. For details, see Misclassification Cost Matrix, Prior Probabilities, and Observation Weights.

References

[1] Rahimi, A., and B. Recht. “Random Features for Large-Scale Kernel Machines.” Advances in Neural Information Processing Systems. Vol. 20, 2008, pp. 1177–1184.

[2] Le, Q., T. Sarlós, and A. Smola. “Fastfood — Approximating Kernel Expansions in Loglinear Time.” Proceedings of the 30th International Conference on Machine Learning. Vol. 28, No. 3, 2013, pp. 244–252.

[3] Huang, P. S., H. Avron, T. N. Sainath, V. Sindhwani, and B. Ramabhadran. “Kernel methods match Deep Neural Networks on TIMIT.” 2014 IEEE International Conference on Acoustics, Speech and Signal Processing. 2014, pp. 205–209.

Extended Capabilities

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

The fitckernel function supports tall arrays with the following usage notes and limitations:

fitckernel does not support tall table data.
Some name-value pair arguments have different defaults compared to the default values for the in-memory fitckernel function. Supported name-value pair arguments, and any differences, are:
- 'Learner'
- 'NumExpansionDimensions'
- 'KernelScale'
- 'BoxConstraint'
- 'Lambda'
- 'BetaTolerance' — Default value is relaxed to 1e–3.
- 'GradientTolerance' — Default value is relaxed to 1e–5.
- 'IterationLimit' — Default value is relaxed to 20.
- 'BlockSize'
- 'RandomStream'
- 'HessianHistorySize'
- 'Verbose' — Default value is 1.
- 'ClassNames'
- 'Cost'
- 'Prior'
- 'ScoreTransform'
- 'Weights' — Value must be a tall array.
- 'OptimizeHyperparameters'
- 'HyperparameterOptimizationOptions' — For cross-validation, tall optimization supports only 'Holdout' validation. By default, the software selects and reserves 20% of the data as holdout validation data, and trains the model using the rest of the data. You can specify a different value for the holdout fraction by using this argument. For example, specify 'HyperparameterOptimizationOptions',struct('Holdout',0.3) to reserve 30% of the data as validation data.
If 'KernelScale' is 'auto', then fitckernel uses the random stream controlled by tallrng for subsampling. For reproducibility, you must set a random number seed for both the global stream and the random stream controlled by tallrng.
If 'Lambda' is 'auto', then fitckernel might take an extra pass through the data to calculate the number of observations in X.
fitckernel uses a block-wise strategy. For details, see Algorithms.

For more information, see Tall Arrays.

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

To perform parallel hyperparameter optimization, use the UseParallel=true option in the HyperparameterOptimizationOptions name-value argument in the call to the fitckernel function.

For more information on parallel hyperparameter optimization, see Parallel Bayesian Optimization.

For general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).

Version History

Introduced in R2017b

expand all

R2023b: Kernel models support standardization of predictors

Starting in R2023b, fitckernel supports the standardization of numeric predictors. That is, you can specify the Standardize value as true to center and scale each numeric predictor variable by the corresponding column mean and standard deviation. The software does not standardize the categorical predictors.

You can also optimize the Standardize hyperparameter by using the OptimizeHyperparameters name-value argument. Unlike in previous releases, when you specify "auto" as the OptimizeHyperparameters value, fitckernel includes Standardize as an optimizable hyperparameter.

fitckernel

Syntax

Description

Examples

Train Kernel Classification Model

Cross-Validate Kernel Classification Model

Optimize Kernel Classifier

Input Arguments

X — Predictor data numeric matrix

Y — Class labels categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

Tbl — Sample data table

ResponseVarName — Response variable name name of variable in Tbl

formula — Explanatory model of response variable and subset of predictor variables character vector | string scalar

Name-Value Arguments

Learner — Linear classification model type 'svm' (default) | 'logistic'

NumExpansionDimensions — Number of dimensions of expanded space 'auto' (default) | positive integer

KernelScale — Kernel scale parameter 1 (default) | "auto" | positive scalar

BoxConstraint — Box constraint 1 (default) | positive scalar

Lambda — Regularization term strength 'auto' (default) | nonnegative scalar

Standardize — Flag to standardize predictor data false or 0 (default) | true or 1

CrossVal — Flag to train cross-validated classifier 'off' (default) | 'on'

CVPartition — Cross-validation partition [] (default) | cvpartition object

Holdout — Fraction of data for holdout validation scalar value in the range (0,1)

KFold — Number of folds 10 (default) | positive integer value greater than 1

Leaveout — Leave-one-out cross-validation flag 'off' (default) | 'on'

BetaTolerance — Relative tolerance on linear coefficients and bias term 1e–4 (default) | nonnegative scalar

GradientTolerance — Absolute gradient tolerance 1e–6 (default) | nonnegative scalar

IterationLimit — Maximum number of optimization iterations positive integer

BlockSize — Maximum amount of allocated memory 4e^3 (4GB) (default) | positive scalar

RandomStream — Random number stream global stream (default) | random stream object

HessianHistorySize — Size of history buffer for Hessian approximation 15 (default) | positive integer

Verbose — Verbosity level 0 (default) | 1

CategoricalPredictors — Categorical predictors list vector of positive integers | logical vector | character matrix | string array | cell array of character vectors | 'all'

ClassNames — Names of classes to use for training categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

Cost — Misclassification cost square matrix | structure array

PredictorNames — Predictor variable names string array of unique names | cell array of unique character vectors

Prior — Prior probabilities 'empirical' (default) | 'uniform' | numeric vector | structure array

ResponseName — Response variable name "Y" (default) | character vector | string scalar

ScoreTransform — Score transformation "none" (default) | "doublelogit" | "invlogit" | "ismax" | "logit" | function handle | ...

Weights — Observation weights nonnegative numeric vector | name of variable in Tbl

OptimizeHyperparameters — Parameters to optimize 'none' (default) | 'auto' | 'all' | string array or cell array of eligible parameter names | vector of optimizableVariable objects

HyperparameterOptimizationOptions — Options for optimization HyperparameterOptimizationOptions object | structure

Output Arguments

Mdl — Trained kernel classification model ClassificationKernel model object | ClassificationPartitionedKernel cross-validated model object

AggregateOptimizationResults — Aggregate optimization results AggregateBayesianOptimization object

FitInfo — Optimization details structure array

HyperparameterOptimizationResults — Cross-validation optimization of hyperparameters BayesianOptimization object | AggregateBayesianOptimization object | table of hyperparameters and associated values

More About

Random Feature Expansion

Box Constraint

Tips

Algorithms

References

Extended Capabilities

Tall Arrays Calculate with arrays that have more rows than fit in memory.

Automatic Parallel Support Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

Version History

R2023b: Kernel models support standardization of predictors

See Also

Topics

`X` — Predictor data
numeric matrix

`Y` — Class labels
categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

`Tbl` — Sample data
table

`ResponseVarName` — Response variable name
name of variable in `Tbl`

`formula` — Explanatory model of response variable and subset of predictor variables
character vector | string scalar

`Learner` — Linear classification model type
`'svm'` (default) | `'logistic'`

`NumExpansionDimensions` — Number of dimensions of expanded space
`'auto'` (default) | positive integer

`KernelScale` — Kernel scale parameter
`1` (default) | `"auto"` | positive scalar

`BoxConstraint` — Box constraint
1 (default) | positive scalar

`Lambda` — Regularization term strength
`'auto'` (default) | nonnegative scalar

`Standardize` — Flag to standardize predictor data
`false` or `0` (default) | `true` or `1`

`CrossVal` — Flag to train cross-validated classifier
`'off'` (default) | `'on'`

`CVPartition` — Cross-validation partition
`[]` (default) | `cvpartition` object

`Holdout` — Fraction of data for holdout validation
scalar value in the range (0,1)

`KFold` — Number of folds
`10` (default) | positive integer value greater than 1

`Leaveout` — Leave-one-out cross-validation flag
`'off'` (default) | `'on'`

`BetaTolerance` — Relative tolerance on linear coefficients and bias term
`1e–4` (default) | nonnegative scalar

`GradientTolerance` — Absolute gradient tolerance
`1e–6` (default) | nonnegative scalar

`IterationLimit` — Maximum number of optimization iterations
positive integer

`BlockSize` — Maximum amount of allocated memory
`4e^3` (4GB) (default) | positive scalar

`RandomStream` — Random number stream
global stream (default) | random stream object

`HessianHistorySize` — Size of history buffer for Hessian approximation
`15` (default) | positive integer

`Verbose` — Verbosity level
`0` (default) | `1`

`CategoricalPredictors` — Categorical predictors list
vector of positive integers | logical vector | character matrix | string array | cell array of character vectors | `'all'`

`ClassNames` — Names of classes to use for training
categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

`Cost` — Misclassification cost
square matrix | structure array

`PredictorNames` — Predictor variable names
string array of unique names | cell array of unique character vectors

`Prior` — Prior probabilities
`'empirical'` (default) | `'uniform'` | numeric vector | structure array

`ResponseName` — Response variable name
`"Y"` (default) | character vector | string scalar

`ScoreTransform` — Score transformation
`"none"` (default) | `"doublelogit"` | `"invlogit"` | `"ismax"` | `"logit"` | function handle | ...

`Weights` — Observation weights
nonnegative numeric vector | name of variable in `Tbl`

`OptimizeHyperparameters` — Parameters to optimize
`'none'` (default) | `'auto'` | `'all'` | string array or cell array of eligible parameter names | vector of `optimizableVariable` objects

`HyperparameterOptimizationOptions` — Options for optimization
`HyperparameterOptimizationOptions` object | structure

`Mdl` — Trained kernel classification model
`ClassificationKernel` model object | `ClassificationPartitionedKernel` cross-validated model object

`AggregateOptimizationResults` — Aggregate optimization results
`AggregateBayesianOptimization` object

`FitInfo` — Optimization details
structure array

`HyperparameterOptimizationResults` — Cross-validation optimization of hyperparameters
`BayesianOptimization` object | `AggregateBayesianOptimization` object | table of hyperparameters and associated values

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.