用于二类分类的支持向量机

了解支持向量机

可分离数据
不可分离的数据
核的非线性变换

可分离数据

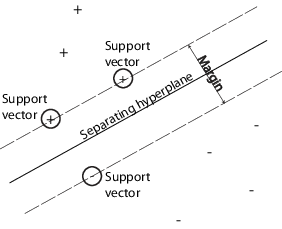
当数据正好有两个类时，可以使用支持向量机 (SVM)。SVM 通过找到将一个类的所有数据点与另一个类的所有数据点分离的最佳超平面对数据进行分类。SVM 的最佳超平面是指使两个类之间的边距最大的超平面。边距是指平行于超平面的内部不含数据点的平板的最大宽度。

支持向量是最接近分离超平面的数据点；这些点在平板的边界上。下图说明了这些定义，其中 + 表示类型 1 的数据点，而 - 表示类型 -1 的数据点。

SVM components including support vectors, hyperplane, and margin

数学表达式：原问题. 此讨论基于 Hastie、Tibshirani 和 Friedman [1] 以及 Christianini 和 Shawe-Taylor [2]的研究。

训练数据是一组点（向量）x_j 及其类别 y_j。对于某个维度 d，x_j ∊ R^d 且 y_j = ±1。超平面的方程是

$f (x) = x' β + b = 0$

其中 β ∊ R^d 和 b 是实数。

以下问题定义最佳分离超平面（即决策边界）。计算使 ||β|| 最小的 β 和 b，使得所有数据点 (x_j,y_j) 满足

$y_{j} f (x_{j}) \geq 1.$

支持向量是边界上的 x_j，满足 $y_{j} f (x_{j}) = 1.$

为了数学上的方便，此问题通常表示为等效的最小化 $‖ β ‖$ 的问题。这是二次规划问题。最优解 $(\hat{β}, \hat{b})$ 能够对向量 z 进行如下分类：

$class (z) = sign (z' \hat{β} + \hat{b}) = sign (\hat{f} (z)) .$

$\hat{f} (z)$ 是分类分数，表示 z 与决策边界的距离。

数学表达式：对偶问题. 求解对偶二次规划问题在计算上更简单。要获得对偶问题，将正的 Lagrange 乘数 α_j 乘以每个约束，然后从目标函数中减去它们：

$L_{P} = \frac{1}{2} β' β - \sum_{j} α_{j} (y_{j} (x_{j}' β + b) - 1),$

您要从中计算 L_P 在 β 和 b 上的平稳点。将 L_P 的梯度设置为 0，您将获得

\begin{matrix} β = \sum_{j} α_{j} y_{j} x_{j} \\ 0 = \sum_{j} α_{j} y_{j} . \end{matrix}

(1)

代入 L_P，您将获得对偶问题 L_D：

$L_{D} = \sum_{j} α_{j} - \frac{1}{2} \sum_{j} \sum_{k} α_{j} α_{k} y_{j} y_{k} x_{j}' x_{k},$

您需要求 α_j ≥ 0 上的最大值。一般情况下，许多 α_j 在最大值时为 0。对偶问题解中非零的 α_j 定义超平面，如公式 1 所示，这可以得出 β 成为 α_jy_jx_j 的总和。对应于非零 α_j 的数据点 x_j 是支持向量。

L_D 关于非零 α_j 的导数在最佳情况下为 0。这可得出

$y_{j} f (x_{j}) - 1 = 0.$

具体来说，通过取非零 α_j 作为任何 j 的值，可得出 b 在解处的值。

此对偶问题是标准的二次规划问题。Optimization Toolbox™ quadprog (Optimization Toolbox) 求解器可用于求解这类问题。

不可分离的数据

您的数据可能不存在一个分离超平面。在这种情况下，SVM 可以使用软边距，获取一个可分离许多数据点，但并非所有数据点的超平面。

软边距有两个标准表达式。两者都包括添加松弛变量 ξ_j 和罚分参数 C。

L¹-范数问题是：
$\min_{β, b, ξ} (\frac{1}{2} β' β + C \sum_{j} ξ_{j})$
满足
$\begin{matrix} y_{j} f (x_{j}) \geq 1 - ξ_{j} \\ ξ_{j} \geq 0. \end{matrix}$
L¹-范数表示使用 ξ_j （而不是其平方）作为松弛变量。fitcsvm 的三个求解器选项 SMO、ISDA 和 L1QP 可求解 L¹-范数最小化问题。
L²-范数问题是：
$\min_{β, b, ξ} (\frac{1}{2} β' β + C \sum_{j} ξ_{j}^{2})$
受限于同样的约束。

在这些公式中，您可以看到，增加 C 会增加松弛变量 ξ_j 的权重，这意味着优化尝试在类之间进行更严格的分离。等效地，将 C 朝 0 方向减少会降低误分类的重要性。

数学表达式：对偶问题. 为了便于计算，这里使用软边距的 L¹ 对偶问题表达式。使用 Lagrange 乘数 μ_j，可得到 L¹-范数最小化问题的函数：

$L_{P} = \frac{1}{2} β' β + C \sum_{j} ξ_{j} - \sum_{j} α_{j} (y_{i} f (x_{j}) - (1 - ξ_{j})) - \sum_{j} μ_{j} ξ_{j},$

您要从中计算 L_P 在 β、b 和正 ξ_j 上的平稳点。将 L_P 的梯度设置为 0，您将获得

$\begin{matrix} β = \sum_{j} α_{j} y_{j} x_{j} \\ \sum_{j} α_{j} y_{j} = 0 \\ α_{j} = C - μ_{j} \\ α_{j}, μ_{j}, ξ_{j} \geq 0. \end{matrix}$

通过这些方程可直接获取对偶问题表达式：

$\max_{α} \sum_{j} α_{j} - \frac{1}{2} \sum_{j} \sum_{k} α_{j} α_{k} y_{j} y_{k} x_{j}' x_{k}$

它受限于以下约束

$\begin{array}{l} \sum_{j} y_{j} α_{j} = 0 \\ 0 \leq α_{j} \leq C . \end{array}$

最后一组不等式 0 ≤ α_j ≤ C 说明了为什么 C 有时称为框约束。C 将 Lagrange 乘数 α_j 的允许值保持在一个“框”中，即有界区域内。

b 的梯度方程给出了对应于支持向量的非零 α_j 集合的解 b。

您可以用类似的方式编写和求解 L²-范数问题的对偶问题。有关详细信息，请参阅 Christianini and Shawe-Taylor [2], Chapter 6。

fitcsvm 实现. 以上两个对偶软边距问题均为二次规划问题。在内部，fitcsvm 提供了几种不同算法来求解这些问题。

对于一类或二类分类，如果您没有设置数据中预期离群值的占比（请参阅 OutlierFraction），则默认求解器是序列最小优化 (SMO)。SMO 通过一系列两点最小化来求解 1-范数最小化问题。在优化过程中，SMO 遵守线性约束 $\sum_{i} α_{i} y_{i} = 0,$ ，并在模型中显式包含偏置项。SMO 相对较快。有关 SMO 的详细信息，请参阅 [3]。
对于二类分类，如果您设置了数据中预期离群值的占比，则默认求解器是迭代单点数据算法。与 SMO 相同，ISDA 用于求解 1-范数问题。与 SMO 不同的是，ISDA 通过一系列单点最小化来进行最小化求解，不遵守线性约束，也不在模型中显式包含偏置项。有关 ISDA 的详细信息，请参阅 [4]。
对于一类或二类分类，如果您有 Optimization Toolbox 许可证，您可以选择使用 quadprog (Optimization Toolbox) 来求解 1-范数问题。quadprog 会占用大量内存，但能以高精度求解二次规划。有关详细信息，请参阅二次规划定义 (Optimization Toolbox)。

核的非线性变换

一些二类分类问题没有简单的超平面作为有用的分离标准。对于这些问题，有一种变通的数学方法可保留 SVM 分离超平面的几乎所有简易性。

这种方法利用了再生核理论的下列成果：

存在一类具有以下属性的函数类 G(x₁,x₂)。存在一个线性空间 S 和将 x 映射到 S 函数 φ，满足
G(x₁,x₂) = <φ(x₁),φ(x₂)>。 (2)
点积发生在空间 S 中。
该类函数包括：
- 多项式：对于某些正整数 p，
  G(x₁,x₂) = (1 + x₁′x₂)^p。 (3)
- 径向基函数（高斯）：
  G(x₁,x₂) = exp(–∥x₁–x₂)∥²)。 (4)
- 多层感知机或 sigmoid（神经网络）：对于正数 p₁ 和负数 p₂，
  G(x₁,x₂) = tanh(p₁x₁′x₂ + p₂)。 (5)
  注意
  并非每组 p₁ 和 p₂ 都能产生有效的再生核。
  fitcsvm 不支持 sigmoid 核。在这种情况下，您可以定义 sigmoid 核，并通过使用 'KernelFunction' 名称-值对组参数来指定它。有关详细信息，请参阅使用自定义核训练 SVM 分类器。

使用核的数学方法依赖于超平面的计算方法。所有超平面分类的计算只使用点积。因此，非线性核可以使用相同的计算和解算法，并获得非线性分类器。得到的分类器是某个空间 S 中的超曲面，但不需要标识或检查空间 S。

使用支持向量机

与任何有监督学习模型一样，您首先训练支持向量机，然后交叉验证分类器。使用经过训练的机器对新数据进行分类（预测）。此外，为了获得令人满意的预测准确度，可以使用各种 SVM 核函数，并且必须调整核函数的参数。

训练 SVM 分类器
用 SVM 分类器对新数据进行分类
调整 SVM 分类器

训练 SVM 分类器

使用 fitcsvm 训练并（可选）交叉验证 SVM 分类器。最常见的语法是：

SVMModel = fitcsvm(X,Y,'KernelFunction','rbf',...
    'Standardize',true,'ClassNames',{'negClass','posClass'});

输入是：

X - 预测变量数据的矩阵，其中每行是一个观测值，每列是一个预测变量。
Y - 类标签数组，其中每行对应于 X 中对应行的值。Y 可以是分类数组、字符数组或字符串数组、逻辑值或数值向量或字符向量元胞数组。
KernelFunction - 二类学习的默认值为 'linear'，它通过超平面分离数据。值 'gaussian'（或 'rbf'）是一类学习的默认值，它指定使用高斯（或径向基函数）核。成功训练 SVM 分类器的重要步骤是选择合适的核函数。
Standardize - 指示软件在训练分类器之前是否应标准化预测变量的标志。
ClassNames - 区分负类和正类，或指定要在数据中包括哪些类。负类是第一个元素（或字符数组的行），例如 'negClass'，正类是第二个元素（或字符数组的行），例如 'posClass'。ClassNames 必须与 Y 具有相同的数据类型。指定类名是很好的做法，尤其是在比较不同分类器的性能时。

生成的训练模型 (SVMModel) 包含来自 SVM 算法的优化参数，使您能够对新数据进行分类。

有关可用于控制训练的更多名称-值对组，请参阅 fitcsvm 参考页。

用 SVM 分类器对新数据进行分类

使用 predict 对新数据进行分类。使用经过训练的 SVM 分类器 (SVMModel) 对新数据进行分类的语法如下：

[label,score] = predict(SVMModel,newX);

生成的向量 label 表示 X 中每行的分类。score 是软分数的 n×2 矩阵。每行对应于 X 中的一行，即新观测值。第一列包含分类为负类的观测值的分数，第二列包含分类为正类的观测值的分数。

要估计后验概率而不是分数，请首先将经过训练的 SVM 分类器 (SVMModel) 传递给 fitPosterior，该方法对分数进行分数-后验概率变换函数拟合。语法是：

ScoreSVMModel = fitPosterior(SVMModel,X,Y);

分类器 ScoreSVMModel 的属性 ScoreTransform 包含最佳变换函数。将 ScoreSVMModel 传递给 predict。输出参数 score 不返回分数，而是包含分类为负类（score 的列 1）或正类（score 的列 2）的观测值的后验概率。

调整 SVM 分类器

使用 fitcsvm 的 'OptimizeHyperparameters' 名称-值对组参数来求得使交叉验证损失最小的参数值。可使用的参数包括 'BoxConstraint'、'KernelFunction'、'KernelScale'、'PolynomialOrder' 和 'Standardize'。有关示例，请参阅使用贝叶斯优化来优化分类器拟合。您也可以使用 bayesopt 函数，如Optimize Cross-Validated Classifier Using bayesopt中所示。bayesopt 函数允许更加灵活地自定义优化。您可以使用 bayesopt 函数优化任何参数，包括使用 fitcsvm 函数时不能优化的参数。

您还可以尝试根据以下方案手动调整分类器的参数：

将数据传递给 fitcsvm，并设置名称-值对组参数 'KernelScale','auto'。假设经过训练的 SVM 模型称为 SVMModel。软件使用启发式过程来选择核尺度。启发式过程使用二次抽样。因此，为了重现结果，在训练分类器之前，请使用 rng 设置随机数种子。
通过将分类器传递给 crossval 以交叉验证分类器。默认情况下，软件进行 10 折交叉验证。
将经过交叉验证的 SVM 模型传递给 kfoldLoss 以估计和保留分类误差。
重新训练 SVM 分类器，但调整 'KernelScale' 和 'BoxConstraint' 名称-值对组参数。
- BoxConstraint - 一种策略是尝试框约束参数的等比数列。例如，取依次增长 10 倍的 11 个值，从 1e-5 到 1e5。增加 BoxConstraint 可能会减少支持向量的数量，但也会增加训练时间。
- KernelScale - 一种策略是尝试基于原始核尺度缩放的 RBF sigma 参数的等比数列。为此，请执行以下操作：
  1. 使用圆点表示法检索原始核尺度，例如 ks：ks = SVMModel.KernelParameters.Scale。
  2. 将原始核尺度的缩放值用作新的核尺度。例如，将 ks 乘以逐项递增 10 倍的 11 个值，从 1e-5 到 1e5。

选择产生最低分类误差的模型。您可能需要进一步细化参数以获得更高的准确度。从初始参数开始，执行另一个交叉验证步骤，这次使用因子 1.2。

用高斯核训练 SVM 分类器

打开实时脚本

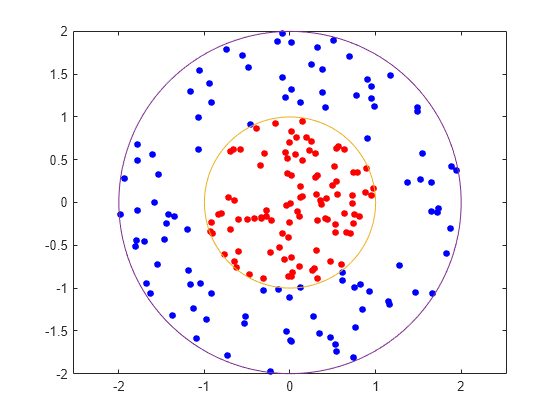
此示例说明如何使用高斯核函数生成非线性分类器。首先，在二维单位圆盘内生成一个由点组成的类，在半径为 1 到半径为 2 的环形空间内生成另一个由点组成的类。然后，使用高斯径向基函数核基于数据生成一个分类器。默认的线性分类器显然不适合此问题，因为模型具有圆对称特性。将框约束参数设置为 Inf 以进行严格分类，这意味着没有误分类的训练点。其他核函数可能无法使用这一严格的框约束，因为它们可能无法提供严格的分类。即使 rbf 分类器可以将类分离，结果也可能会过度训练。

生成在单位圆盘上均匀分布的 100 个点。为此，可先计算均匀随机变量的平方根以得到半径 r，并在 (0, $2 π$ ) 中均匀生成角度 t，然后将点置于 (r cos(t), r sin(t)) 位置上。

rng(1); % For reproducibility
r = sqrt(rand(100,1)); % Radius
t = 2*pi*rand(100,1);  % Angle
data1 = [r.*cos(t), r.*sin(t)]; % Points

生成在环形空间中均匀分布的 100 个点。半径同样与平方根成正比，这次采用从 1 到 4 均匀分布值的平方根。

r2 = sqrt(3*rand(100,1)+1); % Radius
t2 = 2*pi*rand(100,1);      % Angle
data2 = [r2.*cos(t2), r2.*sin(t2)]; % points

绘制各点，并绘制半径为 1 和 2 的圆进行比较。

figure;
plot(data1(:,1),data1(:,2),'r.','MarkerSize',15)
hold on
plot(data2(:,1),data2(:,2),'b.','MarkerSize',15)
ezpolar(@(x)1);ezpolar(@(x)2);
axis equal
hold off

Figure contains an axes object. The axes object contains 6 objects of type line, text. One or more of the lines displays its values using only markers

将数据放在一个矩阵中，并建立一个分类向量。

data3 = [data1;data2];
theclass = ones(200,1);
theclass(1:100) = -1;

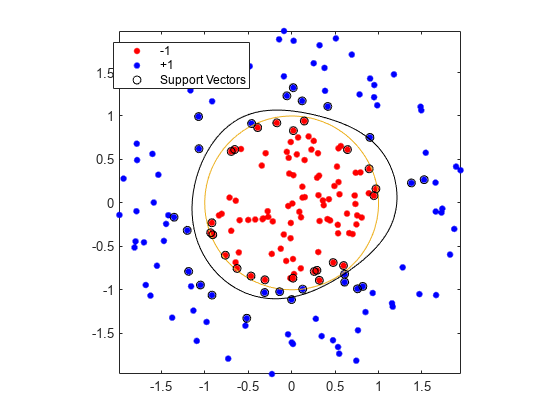
将 KernelFunction 设置为 'rbf'，BoxConstraint 设置为 Inf 以训练 SVM 分类器。绘制决策边界并标记支持向量。

%Train the SVM Classifier
cl = fitcsvm(data3,theclass,'KernelFunction','rbf',...
    'BoxConstraint',Inf,'ClassNames',[-1,1]);

% Predict scores over the grid
d = 0.02;
[x1Grid,x2Grid] = meshgrid(min(data3(:,1)):d:max(data3(:,1)),...
    min(data3(:,2)):d:max(data3(:,2)));
xGrid = [x1Grid(:),x2Grid(:)];
[~,scores] = predict(cl,xGrid);

% Plot the data and the decision boundary
figure;
h(1:2) = gscatter(data3(:,1),data3(:,2),theclass,'rb','.');
hold on
ezpolar(@(x)1);
h(3) = plot(data3(cl.IsSupportVector,1),data3(cl.IsSupportVector,2),'ko');
contour(x1Grid,x2Grid,reshape(scores(:,2),size(x1Grid)),[0 0],'k');
legend(h,{'-1','+1','Support Vectors'});
axis equal
hold off

Figure contains an axes object. The axes object contains 6 objects of type line, text, contour. One or more of the lines displays its values using only markers These objects represent -1, +1, Support Vectors.

fitcsvm 生成一个接近半径为 1 的圆的分类器。差异是随机训练数据造成的。

使用默认参数进行训练会形成更接近圆形的分类边界，但会对一些训练数据进行误分类。此外，BoxConstraint 的默认值为 1，因此支持向量更多。

cl2 = fitcsvm(data3,theclass,'KernelFunction','rbf');
[~,scores2] = predict(cl2,xGrid);

figure;
h(1:2) = gscatter(data3(:,1),data3(:,2),theclass,'rb','.');
hold on
ezpolar(@(x)1);
h(3) = plot(data3(cl2.IsSupportVector,1),data3(cl2.IsSupportVector,2),'ko');
contour(x1Grid,x2Grid,reshape(scores2(:,2),size(x1Grid)),[0 0],'k');
legend(h,{'-1','+1','Support Vectors'});
axis equal
hold off

使用自定义核训练 SVM 分类器

打开脚本

此示例说明如何使用自定义核函数（例如 sigmoid 核）训练 SVM 分类器，并调整自定义核函数参数。

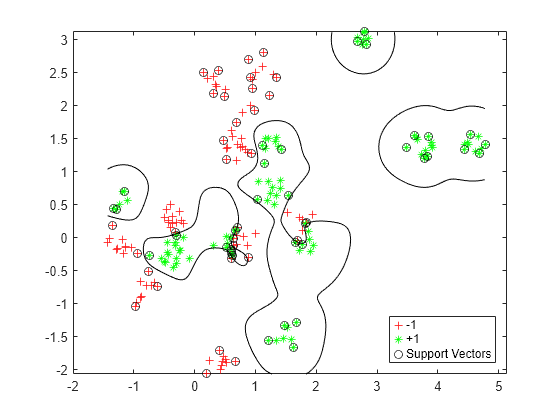
在单位圆内生成一组随机点。将第一和第三象限中的点标记为属于正类，将第二和第四象限中的点标记为属于负类。

rng(1);  % For reproducibility
n = 100; % Number of points per quadrant

r1 = sqrt(rand(2*n,1));                     % Random radii
t1 = [pi/2*rand(n,1); (pi/2*rand(n,1)+pi)]; % Random angles for Q1 and Q3
X1 = [r1.*cos(t1) r1.*sin(t1)];             % Polar-to-Cartesian conversion

r2 = sqrt(rand(2*n,1));
t2 = [pi/2*rand(n,1)+pi/2; (pi/2*rand(n,1)-pi/2)]; % Random angles for Q2 and Q4
X2 = [r2.*cos(t2) r2.*sin(t2)];

X = [X1; X2];        % Predictors
Y = ones(4*n,1);
Y(2*n + 1:end) = -1; % Labels

绘制数据图。

figure;
gscatter(X(:,1),X(:,2),Y);
title('Scatter Diagram of Simulated Data')

编写一个函数，该函数接受特征空间中的两个矩阵作为输入，并使用 sigmoid 核将它们转换为 Gram 矩阵。

function G = mysigmoid(U,V)
% Sigmoid kernel function with slope gamma and intercept c
gamma = 1;
c = -1;
G = tanh(gamma*U*V' + c);
end

将此代码保存为您的 MATLAB® 路径上名为 mysigmoid 的文件。

使用 sigmoid 核函数训练 SVM 分类器。标准化数据是一种良好的做法。

Mdl1 = fitcsvm(X,Y,'KernelFunction','mysigmoid','Standardize',true);

Mdl1 是 ClassificationSVM 分类器，其中包含估计的参数。

绘制数据，并确定支持向量和决策边界。

    % Compute the scores over a grid
d = 0.02; % Step size of the grid
[x1Grid,x2Grid] = meshgrid(min(X(:,1)):d:max(X(:,1)),...
    min(X(:,2)):d:max(X(:,2)));
xGrid = [x1Grid(:),x2Grid(:)];        % The grid
[~,scores1] = predict(Mdl1,xGrid); % The scores

figure;
h(1:2) = gscatter(X(:,1),X(:,2),Y);
hold on
h(3) = plot(X(Mdl1.IsSupportVector,1),...
    X(Mdl1.IsSupportVector,2),'ko','MarkerSize',10);
    % Support vectors
contour(x1Grid,x2Grid,reshape(scores1(:,2),size(x1Grid)),[0 0],'k');
    % Decision boundary
title('Scatter Diagram with the Decision Boundary')
legend({'-1','1','Support Vectors'},'Location','Best');
hold off

您可以调整核参数，尝试改进决策边界的形状。这也可能降低样本内的误分类率，但您应首先确定样本外的误分类率。

使用 10 折交叉验证确定样本外的误分类率。

CVMdl1 = crossval(Mdl1);
misclass1 = kfoldLoss(CVMdl1);
misclass1

misclass1 =

    0.1350

样本外的误分类率为 13.5%。

编写另一个 sigmoid 函数，但设置 gamma = 0.5;。

function G = mysigmoid2(U,V)
% Sigmoid kernel function with slope gamma and intercept c
gamma = 0.5;
c = -1;
G = tanh(gamma*U*V' + c);
end

将此代码保存为您的 MATLAB® 路径上名为 mysigmoid2 的文件。

使用调整后的 sigmoid 核训练另一个 SVM 分类器。绘制数据和决策区域，并确定样本外的误分类率。

Mdl2 = fitcsvm(X,Y,'KernelFunction','mysigmoid2','Standardize',true);
[~,scores2] = predict(Mdl2,xGrid);

figure;
h(1:2) = gscatter(X(:,1),X(:,2),Y);
hold on
h(3) = plot(X(Mdl2.IsSupportVector,1),...
    X(Mdl2.IsSupportVector,2),'ko','MarkerSize',10);
title('Scatter Diagram with the Decision Boundary')
contour(x1Grid,x2Grid,reshape(scores2(:,2),size(x1Grid)),[0 0],'k');
legend({'-1','1','Support Vectors'},'Location','Best');
hold off

CVMdl2 = crossval(Mdl2);
misclass2 = kfoldLoss(CVMdl2);
misclass2

misclass2 =

    0.0450

在 sigmoid 斜率调整后，新决策边界似乎提供更好的样本内拟合，交叉验证率收缩 66% 以上。

使用贝叶斯优化来优化分类器拟合

打开实时脚本

此示例说明如何使用 fitcsvm 函数和 OptimizeHyperparameters 名称-值参数优化 SVM 分类。

生成数据

该分类基于高斯混合模型中点的位置来工作。有关该模型的描述，请参阅 The Elements of Statistical Learning，作者 Hastie、Tibshirani 和 Friedman (2009)，第 17 页。该模型从为“green”类生成 10 个基点开始，这些基点呈二维独立正态分布，均值为 (1,0) 且具有单位方差。它还为“red”类生成 10 个基点，这些基点呈二维独立正态分布，均值为 (0,1) 且具有单位方差。对于每个类（green 和 red），生成 100 个随机点，如下所示：

随机均匀选择合适颜色的一个基点 m。
生成一个呈二维正态分布的独立随机点，其均值为 m，方差为 I/5，其中 I 是 2×2 单位矩阵。在此示例中，使用方差 I/50 来更清楚地显示优化的优势。

为每个类生成 10 个基点。

rng('default') % For reproducibility
grnpop = mvnrnd([1,0],eye(2),10);
redpop = mvnrnd([0,1],eye(2),10);

查看基点。

plot(grnpop(:,1),grnpop(:,2),'go')
hold on
plot(redpop(:,1),redpop(:,2),'ro')
hold off

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

由于一些红色基点靠近绿色基点，因此很难仅基于位置对数据点进行分类。

生成每个类的 100 个数据点。

redpts = zeros(100,2);
grnpts = redpts;
for i = 1:100
    grnpts(i,:) = mvnrnd(grnpop(randi(10),:),eye(2)*0.02);
    redpts(i,:) = mvnrnd(redpop(randi(10),:),eye(2)*0.02);
end

查看数据点。

figure
plot(grnpts(:,1),grnpts(:,2),'go')
hold on
plot(redpts(:,1),redpts(:,2),'ro')
hold off

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

为分类准备数据

将数据放入一个矩阵中，并创建向量 grp，该向量标记每个点的类。1 表示绿色类，-1 表示红色类。

cdata = [grnpts;redpts];
grp = ones(200,1);
grp(101:200) = -1;

准备交叉验证

为交叉验证设置一个分区。

c = cvpartition(200,'KFold',10);

此步骤是可选的。如果您为优化指定一个分区，则您可以为返回的模型计算实际交叉验证损失。

优化拟合

要找到好的拟合，即具有使交叉验证损失最小化的最佳超参数的拟合，请使用贝叶斯优化。使用 OptimizeHyperparameters 名称-值参数指定要优化的超参数列表，并使用 HyperparameterOptimizationOptions 名称-值参数指定优化选项。

将 'OptimizeHyperparameters' 指定为 'auto'。'auto' 选项包括一组典型的要优化的超参数。fitcsvm 查找 BoxConstraint 和 KernelScale 的最佳值。设置超参数优化选项，以使用交叉验证分区 c 并选择 'expected-improvement-plus' 采集函数以实现可再现性。默认采集函数取决于运行时间，因此可以给出不同结果。

opts = struct('CVPartition',c,'AcquisitionFunctionName','expected-improvement-plus');
Mdl = fitcsvm(cdata,grp,'KernelFunction','rbf', ...
    'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions',opts)

|=====================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   | BoxConstraint|  KernelScale |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|    1 | Best   |       0.345 |      0.3453 |       0.345 |       0.345 |      0.00474 |       306.44 |
|    2 | Best   |       0.115 |     0.19547 |       0.115 |     0.12678 |       430.31 |       1.4864 |
|    3 | Accept |        0.52 |     0.23725 |       0.115 |      0.1152 |     0.028415 |     0.014369 |
|    4 | Accept |        0.61 |     0.40438 |       0.115 |     0.11504 |       133.94 |    0.0031427 |
|    5 | Accept |        0.34 |     0.41861 |       0.115 |     0.11504 |     0.010993 |       5.7742 |
|    6 | Best   |       0.085 |     0.25437 |       0.085 |    0.085039 |       885.63 |      0.68403 |
|    7 | Accept |       0.105 |     0.45659 |       0.085 |    0.085428 |       0.3057 |      0.58118 |
|    8 | Accept |        0.21 |     0.21711 |       0.085 |     0.09566 |      0.16044 |      0.91824 |
|    9 | Accept |       0.085 |     0.24955 |       0.085 |     0.08725 |       972.19 |      0.46259 |
|   10 | Accept |         0.1 |     0.24517 |       0.085 |    0.090952 |       990.29 |        0.491 |
|   11 | Best   |        0.08 |     0.29639 |        0.08 |    0.079362 |       2.5195 |        0.291 |
|   12 | Accept |        0.09 |     0.42467 |        0.08 |     0.08402 |       14.338 |      0.44386 |
|   13 | Accept |         0.1 |     0.38996 |        0.08 |     0.08508 |    0.0022577 |      0.23803 |
|   14 | Accept |        0.11 |     0.26937 |        0.08 |    0.087378 |       0.2115 |      0.32109 |
|   15 | Best   |        0.07 |     0.42963 |        0.07 |    0.081507 |        910.2 |      0.25218 |
|   16 | Best   |       0.065 |     0.23488 |       0.065 |    0.072457 |       953.22 |      0.26253 |
|   17 | Accept |       0.075 |      0.2444 |       0.065 |    0.072554 |       998.74 |      0.23087 |
|   18 | Accept |       0.295 |     0.26116 |       0.065 |    0.072647 |       996.18 |       44.626 |
|   19 | Accept |        0.07 |     0.28217 |       0.065 |     0.06946 |       985.37 |      0.27389 |
|   20 | Accept |       0.165 |      0.2219 |       0.065 |    0.071622 |     0.065103 |      0.13679 |
|=====================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   | BoxConstraint|  KernelScale |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|   21 | Accept |       0.345 |      0.3754 |       0.065 |    0.071764 |        971.7 |       999.01 |
|   22 | Accept |        0.61 |     0.17453 |       0.065 |    0.071967 |    0.0010168 |    0.0010005 |
|   23 | Accept |       0.345 |     0.23827 |       0.065 |    0.071959 |    0.0011459 |       995.89 |
|   24 | Accept |        0.35 |     0.19654 |       0.065 |    0.071863 |    0.0010003 |       40.628 |
|   25 | Accept |        0.24 |     0.58861 |       0.065 |    0.072124 |       996.55 |       10.423 |
|   26 | Accept |        0.61 |     0.48935 |       0.065 |    0.072067 |       994.71 |    0.0010063 |
|   27 | Accept |        0.47 |     0.20767 |       0.065 |     0.07218 |       993.69 |     0.029723 |
|   28 | Accept |         0.3 |     0.27163 |       0.065 |    0.072291 |       993.15 |       170.01 |
|   29 | Accept |        0.16 |     0.43589 |       0.065 |    0.072103 |       992.81 |       3.8594 |
|   30 | Accept |       0.365 |     0.29563 |       0.065 |    0.072112 |    0.0010017 |     0.044287 |

Figure contains an axes object. The axes object with title Min objective vs. Number of function evaluations, xlabel Function evaluations, ylabel Min objective contains 2 objects of type line. These objects represent Min observed objective, Estimated min objective.

Figure contains an axes object. The axes object with title Objective function model, xlabel BoxConstraint, ylabel KernelScale contains 5 objects of type line, surface, contour. One or more of the lines displays its values using only markers These objects represent Observed points, Model mean, Next point, Model minimum feasible.

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 50.7264 seconds
Total objective function evaluation time: 9.3519

Best observed feasible point:
    BoxConstraint    KernelScale
    _____________    ___________

       953.22          0.26253  

Observed objective function value = 0.065
Estimated objective function value = 0.073726
Function evaluation time = 0.23488

Best estimated feasible point (according to models):
    BoxConstraint    KernelScale
    _____________    ___________

       985.37          0.27389  

Estimated objective function value = 0.072112
Estimated function evaluation time = 0.29639

Mdl = 
  ClassificationSVM
                         ResponseName: 'Y'
                CategoricalPredictors: []
                           ClassNames: [-1 1]
                       ScoreTransform: 'none'
                      NumObservations: 200
    HyperparameterOptimizationResults: [1x1 BayesianOptimization]
                                Alpha: [77x1 double]
                                 Bias: -0.2352
                     KernelParameters: [1x1 struct]
                       BoxConstraints: [200x1 double]
                      ConvergenceInfo: [1x1 struct]
                      IsSupportVector: [200x1 logical]
                               Solver: 'SMO'


  Properties, Methods

fitcsvm 返回使用最佳估计可行点的 ClassificationSVM 模型对象。最佳估计可行点是基于贝叶斯优化过程的基础高斯过程模型最小化交叉验证损失的置信边界上限的超参数集。

贝叶斯优化过程在内部维护目标函数的高斯过程模型。目标函数是分类的交叉验证误分类率。对于每次迭代，优化过程都会更新高斯过程模型并使用该模型找到一组新的超参数。迭代输出的每行显示新的超参数集和这些列值：

Objective - 基于新的超参数集计算的目标函数值。
Objective runtime - 目标函数计算时间。
Eval result - 结果报告，指定为 Accept、Best 或 Error。Accept 表示目标函数返回有限值，Error 表示目标函数返回非有限实数标量值。Best 表示目标函数返回的有限值低于先前计算的目标函数值。
BestSoFar(observed) - 迄今为止计算的最小目标函数值。此值或者是当前迭代的目标函数值（如果当前迭代的 Eval result 值是 Best），或者是前一个 Best 迭代的值。
BestSoFar(estim.) - 在每次迭代中，软件使用更新后的高斯过程模型，基于迄今为止尝试的所有超参数集估计目标函数值的置信边界上限。然后，软件选择具有最小置信边界上限的点。BestSoFar(estim.) 值是 predictObjective 函数在最小值点处返回的目标函数值。

迭代输出下方的图分别以蓝色和绿色显示 BestSoFar(observed) 和 BestSoFar(estim.) 值。

返回的对象 Mdl 使用最佳估计可行点，即基于最终高斯过程模型在最终迭代中产生 BestSoFar(estim.) 值的超参数集。

您可以从 HyperparameterOptimizationResults 属性或使用 bestPoint 函数获得最佳点。

Mdl.HyperparameterOptimizationResults.XAtMinEstimatedObjective

ans=1×2 table
    BoxConstraint    KernelScale
    _____________    ___________

       985.37          0.27389

[x,CriterionValue,iteration] = bestPoint(Mdl.HyperparameterOptimizationResults)

x=1×2 table
    BoxConstraint    KernelScale
    _____________    ___________

       985.37          0.27389

CriterionValue = 0.0888

iteration = 19

默认情况下，bestPoint 函数使用 'min-visited-upper-confidence-interval' 条件。此条件选择从第 19 次迭代获得的超参数作为最佳点。CriterionValue 是最终高斯过程模型计算的交叉验证损失的上界。使用分区 c 计算实际交叉验证损失。

L_MinEstimated = kfoldLoss(fitcsvm(cdata,grp,'CVPartition',c,'KernelFunction','rbf', ...
    'BoxConstraint',x.BoxConstraint,'KernelScale',x.KernelScale))

L_MinEstimated = 0.0700

实际交叉验证损失接近估计值。Estimated objective function value 显示在优化结果图的下方。

您也可以从 HyperparameterOptimizationResults 属性或通过将 Criterion 指定为 'min-observed' 来提取最佳观测可行点（即迭代输出中的最后一个 Best 点）。

Mdl.HyperparameterOptimizationResults.XAtMinObjective

ans=1×2 table
    BoxConstraint    KernelScale
    _____________    ___________

       953.22          0.26253

[x_observed,CriterionValue_observed,iteration_observed] = bestPoint(Mdl.HyperparameterOptimizationResults,'Criterion','min-observed')

x_observed=1×2 table
    BoxConstraint    KernelScale
    _____________    ___________

       953.22          0.26253

CriterionValue_observed = 0.0650

iteration_observed = 16

'min-observed' 条件选择从第 16 次迭代获得的超参数作为最佳点。CriterionValue_observed 是使用所选超参数计算的实际交叉验证损失。有关详细信息，请参阅 bestPoint 的 Criterion 名称-值参数。

可视化经过优化的分类器。

d = 0.02;
[x1Grid,x2Grid] = meshgrid(min(cdata(:,1)):d:max(cdata(:,1)), ...
    min(cdata(:,2)):d:max(cdata(:,2)));
xGrid = [x1Grid(:),x2Grid(:)];
[~,scores] = predict(Mdl,xGrid);

figure
h(1:2) = gscatter(cdata(:,1),cdata(:,2),grp,'rg','+*');
hold on
h(3) = plot(cdata(Mdl.IsSupportVector,1), ...
    cdata(Mdl.IsSupportVector,2),'ko');
contour(x1Grid,x2Grid,reshape(scores(:,2),size(x1Grid)),[0 0],'k');
legend(h,{'-1','+1','Support Vectors'},'Location','Southeast');

Figure contains an axes object. The axes object contains 4 objects of type line, contour. One or more of the lines displays its values using only markers These objects represent -1, +1, Support Vectors.

基于新数据计算准确度

生成并分类新的测试数据点。

grnobj = gmdistribution(grnpop,.2*eye(2));
redobj = gmdistribution(redpop,.2*eye(2));

newData = random(grnobj,10);
newData = [newData;random(redobj,10)];
grpData = ones(20,1); % green = 1
grpData(11:20) = -1; % red = -1

v = predict(Mdl,newData);

基于测试数据集计算误分类率。

L_Test = loss(Mdl,newData,grpData)

L_Test = 0.3500

确定哪些新数据点是分类正确的。将正确分类的点格式化为红色方块，将不正确分类的点格式化为黑色方块。

h(4:5) = gscatter(newData(:,1),newData(:,2),v,'mc','**');

mydiff = (v == grpData); % Classified correctly

for ii = mydiff % Plot red squares around correct pts
    h(6) = plot(newData(ii,1),newData(ii,2),'rs','MarkerSize',12);
end

for ii = not(mydiff) % Plot black squares around incorrect pts
    h(7) = plot(newData(ii,1),newData(ii,2),'ks','MarkerSize',12);
end
legend(h,{'-1 (training)','+1 (training)','Support Vectors', ...
    '-1 (classified)','+1 (classified)', ...
    'Correctly Classified','Misclassified'}, ...
    'Location','Southeast');
hold off

Figure contains an axes object. The axes object contains 8 objects of type line, contour. One or more of the lines displays its values using only markers These objects represent -1 (training), +1 (training), Support Vectors, -1 (classified), +1 (classified), Correctly Classified, Misclassified.

绘制 SVM 分类模型的后验概率区域

打开实时脚本

此示例说明如何预测 SVM 模型在观测网格上的后验概率，然后绘制该网格上的后验概率。绘制后验概率会显现出决策边界。

加载 Fisher 鸢尾花数据集。使用花瓣长度和宽度训练分类器，并从数据中删除海滨锦葵物种。

load fisheriris
classKeep = ~strcmp(species,'virginica');
X = meas(classKeep,3:4);
y = species(classKeep);

使用数据训练 SVM 分类器。指定类的顺序是很好的做法。

SVMModel = fitcsvm(X,y,'ClassNames',{'setosa','versicolor'});

估计最佳分数变换函数。

rng(1); % For reproducibility
[SVMModel,ScoreParameters] = fitPosterior(SVMModel);

Warning: Classes are perfectly separated. The optimal score-to-posterior transformation is a step function.

ScoreParameters

ScoreParameters = struct with fields:
                        Type: 'step'
                  LowerBound: -0.8431
                  UpperBound: 0.6897
    PositiveClassProbability: 0.5000

最佳分数变换函数是阶跃函数，因为类是可分离的。ScoreParameters 的字段 LowerBound 和 UpperBound 指示与类分离超平面（边距）内观测值对应的分数区间的下端点和上端点。没有训练观测值落在边距内。如果区间中有一个新分数，则软件会为对应的观测值分配一个正类后验概率，即 ScoreParameters 的 PositiveClassProbability 字段中的值。

在观测到的预测变量空间中定义一个数值网格。预测该网格中每个实例的后验概率。

xMax = max(X);
xMin = min(X);
d = 0.01;
[x1Grid,x2Grid] = meshgrid(xMin(1):d:xMax(1),xMin(2):d:xMax(2));

[~,PosteriorRegion] = predict(SVMModel,[x1Grid(:),x2Grid(:)]);

绘制正类后验概率区域和训练数据。

figure;
contourf(x1Grid,x2Grid,...
        reshape(PosteriorRegion(:,2),size(x1Grid,1),size(x1Grid,2)));
h = colorbar;
h.Label.String = 'P({\it{versicolor}})';
h.YLabel.FontSize = 16;
caxis([0 1]);
colormap jet;

hold on
gscatter(X(:,1),X(:,2),y,'mc','.x',[15,10]);
sv = X(SVMModel.IsSupportVector,:);
plot(sv(:,1),sv(:,2),'yo','MarkerSize',15,'LineWidth',2);
axis tight
hold off

Figure contains an axes object. The axes object contains 4 objects of type contour, line. One or more of the lines displays its values using only markers These objects represent setosa, versicolor.

在二类学习中，如果类是可分离的，则有三个区域：一个是包含正类后验概率为 0 的观测值的区域，另一个是包含正类后验概率为 1 的观测值的区域，还有一个是包含具有正类先验概率的观测值的区域。

使用线性支持向量机分析图像

打开实时脚本

此示例说明如何通过训练由线性 SVM 二类学习器组成的纠错输出编码 (ECOC) 模型来确定形状占据图像的哪个象限。此示例还说明存储支持向量、其标签和估计的 $α$ 系数的 ECOC 模型的磁盘空间消耗。

创建数据集

在一个 50×50 图像中随机放置一个半径为 5 的圆。生成 5000 个图像。为每个图像创建一个标签，指示圆占据的象限。象限 1 在右上角，象限 2 在左上角，象限 3 在左下角，象限 4 在右下角。预测变量是每个像素的强度。

d = 50;  % Height and width of the images in pixels
n = 5e4; % Sample size

X = zeros(n,d^2); % Predictor matrix preallocation 
Y = zeros(n,1);   % Label preallocation
theta = 0:(1/d):(2*pi);
r = 5;            % Circle radius
rng(1);           % For reproducibility

for j = 1:n
    figmat = zeros(d);                       % Empty image
    c = datasample((r + 1):(d - r - 1),2);   % Random circle center
    x = r*cos(theta) + c(1);                 % Make the circle 
    y = r*sin(theta) + c(2);               
    idx = sub2ind([d d],round(y),round(x));  % Convert to linear indexing
    figmat(idx) = 1;                         % Draw the circle
    X(j,:) = figmat(:);                % Store the data
    Y(j) = (c(2) >= floor(d/2)) + 2*(c(2) < floor(d/2)) + ...
        (c(1) < floor(d/2)) + ...
        2*((c(1) >= floor(d/2)) & (c(2) < floor(d/2))); % Determine the quadrant
end

绘制观测值。

figure
imagesc(figmat)
h = gca;
h.YDir = 'normal';
title(sprintf('Quadrant %d',Y(end)))

Figure contains an axes object. The axes object with title Quadrant 1 contains an object of type image.

训练 ECOC 模型

使用 25% 的留出样本，并指定训练和留出样本索引。

p = 0.25;
CVP = cvpartition(Y,'Holdout',p); % Cross-validation data partition
isIdx = training(CVP);            % Training sample indices
oosIdx = test(CVP);               % Test sample indices

创建一个 SVM 模板，它指定存储二类学习器的支持向量。将它和训练数据传递给 fitcecoc 以训练模型。确定训练样本分类误差。

t = templateSVM('SaveSupportVectors',true);
MdlSV = fitcecoc(X(isIdx,:),Y(isIdx),'Learners',t);
isLoss = resubLoss(MdlSV)

isLoss = 0

MdlSV 是经过训练的 ClassificationECOC 多类模型。它存储每个二类学习器的训练数据和支持向量。对于大型数据集，如图像分析中的数据集，该模型会消耗大量内存。

确定 ECOC 模型消耗的磁盘空间量。

infoMdlSV = whos('MdlSV');
mbMdlSV = infoMdlSV.bytes/1.049e6

mbMdlSV = 763.6150

该模型消耗 763.6 MB。

提高模型效率

您可以评估样本外的性能。您还可以使用不包含支持向量、其相关参数和训练数据的压缩模型来评估模型是否过拟合。

从经过训练的 ECOC 模型中丢弃支持向量和相关参数。然后，使用 compact 从生成的模型中丢弃训练数据。

Mdl = discardSupportVectors(MdlSV);
CMdl = compact(Mdl);
info = whos('Mdl','CMdl');
[bytesCMdl,bytesMdl] = info.bytes;
memReduction = 1 - [bytesMdl bytesCMdl]/infoMdlSV.bytes

memReduction = 1×2

    0.0626    0.9996

在本例中，丢弃支持向量可将内存消耗减少大约 6%。压缩和丢弃支持向量会将大小减小大约 99.96%。

管理支持向量的另一种方法是通过指定更大的框约束（如 100）来减少训练过程中的支持向量数量。虽然使用更少支持向量的 SVM 模型更可取并且消耗更少的内存，但增加框约束的值往往会增加训练时间。

从工作区中删除 MdlSV 和 Mdl。

clear Mdl MdlSV

评估留出样本性能

计算留出样本的分类误差。绘制留出样本预测的样本。

oosLoss = loss(CMdl,X(oosIdx,:),Y(oosIdx))

oosLoss = 0

yHat = predict(CMdl,X(oosIdx,:));
nVec = 1:size(X,1);
oosIdx = nVec(oosIdx);

figure;
for j = 1:9
    subplot(3,3,j)
    imagesc(reshape(X(oosIdx(j),:),[d d]))
    h = gca;
    h.YDir = 'normal';
    title(sprintf('Quadrant: %d',yHat(j)))
end
text(-1.33*d,4.5*d + 1,'Predictions','FontSize',17)

该模型不会对任何留出样本观测值进行误分类。

另请参阅

fitcsvm | bayesopt | kfoldLoss

参考

[1] Hastie, T., R. Tibshirani, and J. Friedman. The Elements of Statistical Learning, second edition. New York: Springer, 2008.

[2] Christianini, N., and J. Shawe-Taylor. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge, UK: Cambridge University Press, 2000.

[3] Fan, R.-E., P.-H. Chen, and C.-J. Lin. “Working set selection using second order information for training support vector machines.” Journal of Machine Learning Research, Vol 6, 2005, pp. 1889–1918.

[4] Kecman V., T. -M. Huang, and M. Vogt. “Iterative Single Data Algorithm for Training Kernel Machines from Huge Data Sets: Theory and Performance.” In Support Vector Machines: Theory and Applications. Edited by Lipo Wang, 255–274. Berlin: Springer-Verlag, 2005.