fitcsvm

训练 SVM 分类器

加载 Fisher 鸢尾花数据集。删除萼片的长度和宽度以及所有观测到的山鸢尾花。

load fisheriris
inds = ~strcmp(species,'setosa');
X = meas(inds,3:4);
y = species(inds);

使用经过处理的数据集训练 SVM 分类器。

SVMModel = fitcsvm(X,y)

SVMModel = 
  ClassificationSVM
             ResponseName: 'Y'
    CategoricalPredictors: []
               ClassNames: {'versicolor'  'virginica'}
           ScoreTransform: 'none'
          NumObservations: 100
                    Alpha: [24×1 double]
                     Bias: -14.4149
         KernelParameters: [1×1 struct]
           BoxConstraints: [100×1 double]
          ConvergenceInfo: [1×1 struct]
          IsSupportVector: [100×1 logical]
                   Solver: 'SMO'


  Properties, Methods

SVMModel 是经过训练的 ClassificationSVM 分类器。您可以查看 SVMModel 的属性。例如，使用圆点表示法查看类顺序。

classOrder = SVMModel.ClassNames

classOrder = 2×1 cell
    {'versicolor'}
    {'virginica' }

第一个类 ('versicolor') 是负类，第二个类 ('virginica') 是正类。您可以使用 'ClassNames' 名称-值对组参量在训练期间更改类顺序。

绘制数据的散点图并圈出支持向量。

sv = SVMModel.SupportVectors;
figure
gscatter(X(:,1),X(:,2),y)
hold on
plot(sv(:,1),sv(:,2),'ko','MarkerSize',10)
legend('versicolor','virginica','Support Vector')
hold off

Figure contains an axes object. The axes object contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent versicolor, virginica, Support Vector.

支持向量是发生在其估计的类边界之上或之外的观测值。

您可以使用 'BoxConstraint' 名称-值对组参量在训练过程中设置框约束来调整边界（从而调整支持向量的数量）。

绘制二类 SVM 分类器的决策边界和边际线

此示例说明如何绘制具有两个预测变量的二类（二元）SVM 分类器的决策边界和边距线。

加载 Fisher 鸢尾花数据集。排除所有杂色鸢尾花品种（仅留下山鸢尾花和海滨鸢尾花品种），仅保留萼片长度和宽度测量值。

load fisheriris;
inds = ~strcmp(species,'versicolor');
X = meas(inds,1:2);
s = species(inds);

训练线性核 SVM 分类器。

SVMModel = fitcsvm(X,s);

SVMModel 是经过训练的 ClassificationSVM 分类器，其属性包括支持向量、线性预测变量系数和偏置项。

sv = SVMModel.SupportVectors; % Support vectors
beta = SVMModel.Beta; % Linear predictor coefficients
b = SVMModel.Bias; % Bias term

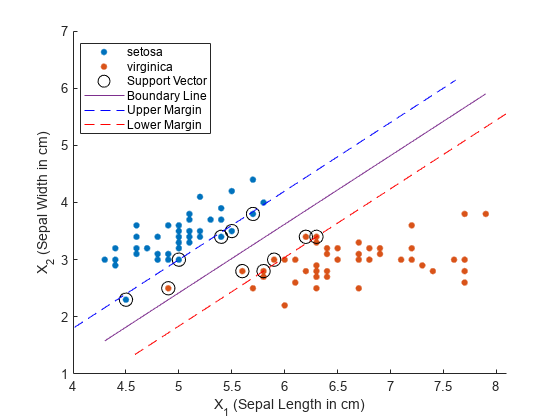
绘制数据的散点图并圈出支持向量。支持向量是发生在其估计的类边界之上或之外的观测值。

hold on
gscatter(X(:,1),X(:,2),s)
plot(sv(:,1),sv(:,2),'ko','MarkerSize',10)

SVMModel 分类器的最佳分离超平面是由 $β_{1} X_{1} + β_{2} X_{2} + b = 0$ 指定的直线。将两个品种之间的决策边界绘制为一条实线。

X1 = linspace(min(X(:,1)),max(X(:,1)),100);
X2 = -(beta(1)/beta(2)*X1)-b/beta(2);
plot(X1,X2,'-')

线性预测变量系数 $β$ 定义与决策边界正交的向量。最大边距宽度为 $2 {| | β ‖}^{- 1}$ （有关详细信息，请参阅用于二类分类的支持向量机）。将最大边距边界绘制为虚线。标记坐标区并添加图例。

m = 1/sqrt(beta(1)^2 + beta(2)^2);  % Margin half-width
X1margin_low = X1+beta(1)*m^2;
X2margin_low = X2+beta(2)*m^2;
X1margin_high = X1-beta(1)*m^2;
X2margin_high = X2-beta(2)*m^2;
plot(X1margin_high,X2margin_high,'b--')
plot(X1margin_low,X2margin_low,'r--')
xlabel('X_1 (Sepal Length in cm)')
ylabel('X_2 (Sepal Width in cm)')
legend('setosa','virginica','Support Vector', ...
    'Boundary Line','Upper Margin','Lower Margin')
hold off

Figure contains an axes object. The axes object with xlabel X_1 (Sepal blank Length blank in blank cm), ylabel X_2 (Sepal blank Width blank in blank cm) contains 6 objects of type line. One or more of the lines displays its values using only markers These objects represent setosa, virginica, Support Vector, Boundary Line, Upper Margin, Lower Margin.

训练和交叉验证 SVM 分类器

加载 ionosphere 数据集。

load ionosphere
rng(1); % For reproducibility

使用径向基核训练 SVM 分类器。让软件计算核函数的缩放值。对预测变量进行标准化。

SVMModel = fitcsvm(X,Y,'Standardize',true,'KernelFunction','RBF',...
    'KernelScale','auto');

SVMModel 是经过训练的 ClassificationSVM 分类器。

交叉验证 SVM 分类器。默认情况下，软件使用 10 折交叉验证。

CVSVMModel = crossval(SVMModel);

CVSVMModel 是 ClassificationPartitionedModel 交叉验证的分类器。

估计样本外的误分类率。

classLoss = kfoldLoss(CVSVMModel)

classLoss = 
0.0484

泛化率约为 5%。

使用 SVM 和一类学习检测离群值

通过将所有鸢尾花分配给同一个类来修改 Fisher 的鸢尾花数据集。检测修改后的数据集中的离群值，并确认观测值中离群值的预期比例。

加载 Fisher 鸢尾花数据集。删除花瓣的长度和宽度。将所有鸢尾花都视为来自同一个类。

load fisheriris
X = meas(:,1:2);
y = ones(size(X,1),1);

使用修改后的数据集训练 SVM 分类器。假设 5% 的观测值是离群值。对预测变量进行标准化。

rng(1);
SVMModel = fitcsvm(X,y,'KernelScale','auto','Standardize',true,...
    'OutlierFraction',0.05);

SVMModel 是经过训练的 ClassificationSVM 分类器。默认情况下，软件使用高斯核进行一类学习。

绘制观测值和决策边界。标记支持向量和潜在离群值。

svInd = SVMModel.IsSupportVector;
h = 0.02; % Mesh grid step size
[X1,X2] = meshgrid(min(X(:,1)):h:max(X(:,1)),...
    min(X(:,2)):h:max(X(:,2)));
[~,score] = predict(SVMModel,[X1(:),X2(:)]);
scoreGrid = reshape(score,size(X1,1),size(X2,2));

figure
plot(X(:,1),X(:,2),'k.')
hold on
plot(X(svInd,1),X(svInd,2),'ro','MarkerSize',10)
contour(X1,X2,scoreGrid)
colorbar;
title('{\bf Iris Outlier Detection via One-Class SVM}')
xlabel('Sepal Length (cm)')
ylabel('Sepal Width (cm)')
legend('Observation','Support Vector')
hold off

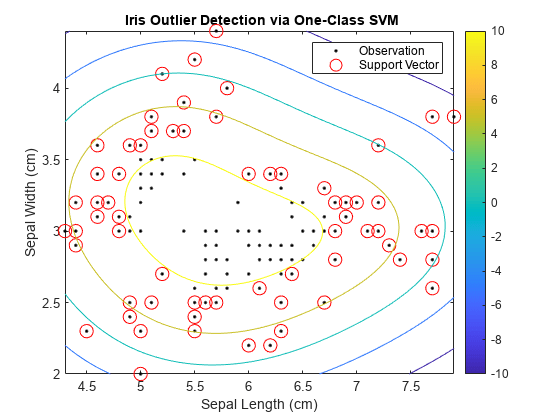
Figure contains an axes object. The axes object with title blank Iris blank Outlier blank Detection blank via blank One-Class blank SVM, xlabel Sepal Length (cm), ylabel Sepal Width (cm) contains 3 objects of type line, contour. One or more of the lines displays its values using only markers These objects represent Observation, Support Vector.

将离群值与其余数据分隔的边界出现在围道值为 0 的位置。

验证交叉验证数据中具有负分数的观测值的比例接近 5%。

CVSVMModel = crossval(SVMModel);
[~,scorePred] = kfoldPredict(CVSVMModel);
outlierRate = mean(scorePred<0)

outlierRate = 
0.0467

使用二类 SVM 计算多个类边界

创建 fisheriris 数据集的散点图。将图中网格的坐标点视为来自数据集分布的新观测值，并通过将坐标点分配给数据集中的三个类之一来找出类边界。

加载 Fisher 鸢尾花数据集。使用花瓣长度和宽度作为预测变量。

load fisheriris
X = meas(:,3:4);
Y = species;

检查数据的散点图。

figure
gscatter(X(:,1),X(:,2),Y);
h = gca;
lims = [h.XLim h.YLim]; % Extract the x and y axis limits
title('{\bf Scatter Diagram of Iris Measurements}');
xlabel('Petal Length (cm)');
ylabel('Petal Width (cm)');
legend('Location','Northwest');

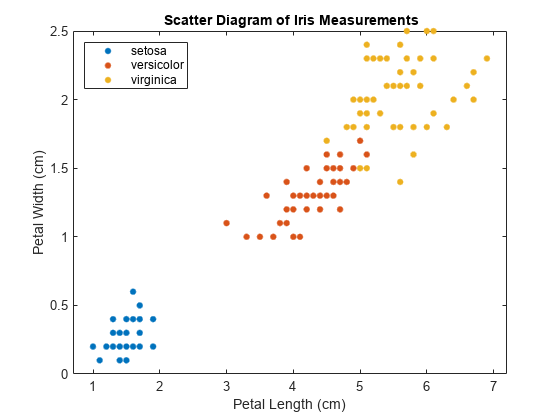
Figure contains an axes object. The axes object with title blank Scatter blank Diagram blank of blank Iris blank Measurements, xlabel Petal Length (cm), ylabel Petal Width (cm) contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent setosa, versicolor, virginica.

该数据包含三个类，其中一个类与其他类可线性分离。

对于每个类：

创建一个逻辑向量 (indx)，指示观测值是否为该类的成员。
使用预测变量数据和 indx 训练 SVM 分类器。
将该分类器存储在元胞数组的一个元胞中。

定义类顺序。

SVMModels = cell(3,1);
classes = unique(Y);
rng(1); % For reproducibility

for j = 1:numel(classes)
    indx = strcmp(Y,classes(j)); % Create binary classes for each classifier
    SVMModels{j} = fitcsvm(X,indx,'ClassNames',[false true],'Standardize',true,...
        'KernelFunction','rbf','BoxConstraint',1);
end

SVMModels 是 3×1 元胞数组，其中每个元胞包含一个 ClassificationSVM 分类器。对于每个元胞，正类分别是 setosa、versicolor 和 virginica。

在图中定义精细网格，并将坐标点视为来自训练数据分布的新观测值。使用每个分类器估计新观测值的分数。

d = 0.02;
[x1Grid,x2Grid] = meshgrid(min(X(:,1)):d:max(X(:,1)),...
    min(X(:,2)):d:max(X(:,2)));
xGrid = [x1Grid(:),x2Grid(:)];
N = size(xGrid,1);
Scores = zeros(N,numel(classes));

for j = 1:numel(classes)
    [~,score] = predict(SVMModels{j},xGrid);
    Scores(:,j) = score(:,2); % Second column contains positive-class scores
end

Scores 的每行包含三个分数。分数最高的元素的索引是新类观测值最可能属于的类的索引。

将每个新观测值与给它最高分数的分类器相关联。

[~,maxScore] = max(Scores,[],2);

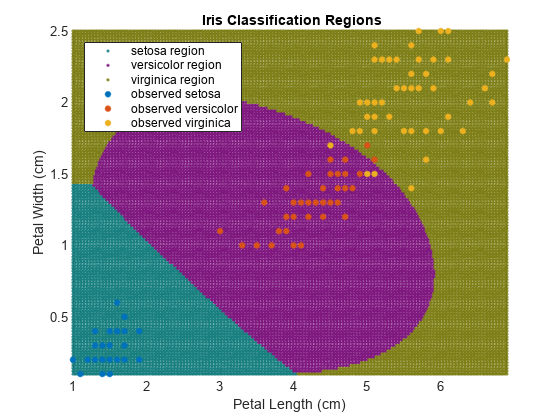
基于对应新观测值所属的类，在绘图区域中着色。

figure
h(1:3) = gscatter(xGrid(:,1),xGrid(:,2),maxScore,...
    [0.1 0.5 0.5; 0.5 0.1 0.5; 0.5 0.5 0.1]);
hold on
h(4:6) = gscatter(X(:,1),X(:,2),Y);
title('{\bf Iris Classification Regions}');
xlabel('Petal Length (cm)');
ylabel('Petal Width (cm)');
legend(h,{'setosa region','versicolor region','virginica region',...
    'observed setosa','observed versicolor','observed virginica'},...
    'Location','Northwest');
axis tight
hold off

Figure contains an axes object. The axes object with title blank Iris blank Classification blank Regions, xlabel Petal Length (cm), ylabel Petal Width (cm) contains 6 objects of type line. One or more of the lines displays its values using only markers These objects represent setosa region, versicolor region, virginica region, observed setosa, observed versicolor, observed virginica.

优化 SVM 分类器

使用 fitcsvm 自动优化超参数。

加载 ionosphere 数据集。

load ionosphere

通过使用自动超参数优化，找到最小化五折交叉验证损失的超参数。为了实现可再现性，请设置随机种子并使用 'expected-improvement-plus' 采集函数。

rng default
Mdl = fitcsvm(X,Y,'OptimizeHyperparameters','auto', ...
    'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName', ...
    'expected-improvement-plus'))

|====================================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   | BoxConstraint|  KernelScale |  Standardize |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |              |
|====================================================================================================================|
|    1 | Best   |     0.35897 |     0.19398 |     0.35897 |     0.35897 |       3.8653 |       961.53 |         true |
|    2 | Best   |     0.12821 |      9.0328 |     0.12821 |     0.15646 |       429.99 |       0.2378 |        false |
|    3 | Accept |     0.35897 |    0.047362 |     0.12821 |      0.1315 |      0.11801 |       8.9479 |        false |
|    4 | Accept |      0.1339 |       4.447 |     0.12821 |     0.12965 |    0.0010694 |    0.0032063 |         true |
|    5 | Accept |     0.15954 |      10.304 |     0.12821 |     0.12824 |       973.65 |      0.15179 |        false |
|    6 | Accept |     0.13675 |     0.21247 |     0.12821 |      0.1283 |       234.28 |       2.8822 |        false |
|    7 | Accept |     0.35897 |    0.064441 |     0.12821 |     0.12826 |     0.005253 |       835.53 |         true |
|    8 | Accept |     0.14245 |      10.593 |     0.12821 |     0.12829 |       91.176 |     0.042696 |        false |
|    9 | Accept |       0.151 |      9.8828 |     0.12821 |     0.12831 |    0.0064316 |    0.0010249 |         true |
|   10 | Accept |      0.1339 |      5.3155 |     0.12821 |     0.12835 |       153.27 |      0.38874 |        false |
|   11 | Accept |     0.26781 |      10.301 |     0.12821 |     0.12948 |       260.21 |     0.001097 |        false |
|   12 | Accept |     0.12821 |     0.16006 |     0.12821 |     0.12935 |    0.0034086 |     0.029311 |         true |
|   13 | Best   |     0.11966 |    0.098343 |     0.11966 |     0.12144 |    0.0010229 |     0.032368 |         true |
|   14 | Accept |     0.35897 |    0.058671 |     0.11966 |     0.12177 |       987.92 |       683.08 |        false |
|   15 | Accept |     0.12821 |    0.090764 |     0.11966 |     0.11979 |    0.0010124 |      0.28112 |         true |
|   16 | Accept |     0.22792 |      10.434 |     0.11966 |     0.11995 |       6.9606 |     0.001715 |         true |
|   17 | Accept |     0.11966 |    0.067735 |     0.11966 |     0.11979 |    0.0010509 |     0.078769 |         true |
|   18 | Accept |     0.12251 |    0.084681 |     0.11966 |     0.12049 |    0.0010131 |     0.054019 |         true |
|   19 | Accept |      0.1339 |      5.1717 |     0.11966 |     0.12071 |      0.08684 |     0.018067 |         true |
|   20 | Accept |     0.11966 |     0.10595 |     0.11966 |     0.12123 |     0.048335 |      0.21846 |         true |
|====================================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   | BoxConstraint|  KernelScale |  Standardize |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |              |
|====================================================================================================================|
|   21 | Accept |     0.11966 |     0.09685 |     0.11966 |     0.12119 |     0.013573 |      0.11789 |         true |
|   22 | Accept |      0.1339 |     0.46169 |     0.11966 |     0.12123 |       1.2995 |      0.26436 |         true |
|   23 | Accept |      0.1396 |      8.7181 |     0.11966 |     0.12127 |    0.0019603 |    0.0010023 |        false |
|   24 | Accept |     0.13675 |      7.1196 |     0.11966 |     0.12136 |      0.17347 |     0.010479 |        false |
|   25 | Accept |     0.14245 |     0.19526 |     0.11966 |     0.11914 |    0.0010001 |    0.0076351 |        false |
|   26 | Accept |     0.12536 |     0.15835 |     0.11966 |     0.12144 |     0.035903 |      0.11247 |         true |
|   27 | Accept |      0.1339 |         3.3 |     0.11966 |     0.12144 |       897.97 |        1.361 |        false |
|   28 | Accept |      0.1339 |      5.0878 |     0.11966 |     0.12146 |       6.6245 |     0.085879 |        false |
|   29 | Accept |     0.12251 |    0.066541 |     0.11966 |      0.1214 |    0.0069215 |      0.12029 |         true |
|   30 | Accept |     0.12251 |      0.1273 |     0.11966 |     0.12136 |     0.049433 |      0.43143 |         true |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 110.3716 seconds
Total objective function evaluation time: 101.9977

Best observed feasible point:
    BoxConstraint    KernelScale    Standardize
    _____________    ___________    ___________

      0.0010229       0.032368         true    

Observed objective function value = 0.11966
Estimated objective function value = 0.12229
Function evaluation time = 0.098343

Best estimated feasible point (according to models):
    BoxConstraint    KernelScale    Standardize
    _____________    ___________    ___________

      0.013573         0.11789         true    

Estimated objective function value = 0.12136
Estimated function evaluation time = 0.092121

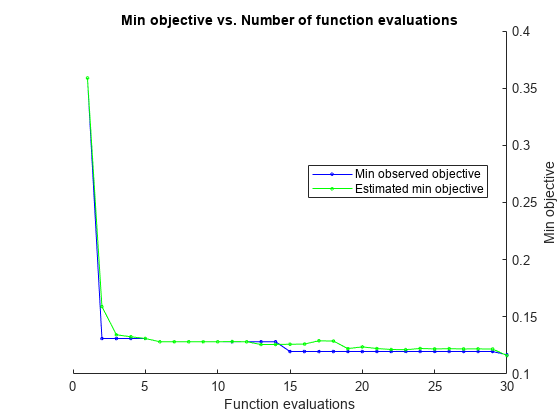
Figure contains an axes object. The axes object with title Min objective vs. Number of function evaluations, xlabel Function evaluations, ylabel Min objective contains 2 objects of type line. These objects represent Min observed objective, Estimated min objective.

Mdl = 
  ClassificationSVM
                         ResponseName: 'Y'
                CategoricalPredictors: []
                           ClassNames: {'b'  'g'}
                       ScoreTransform: 'none'
                      NumObservations: 351
    HyperparameterOptimizationResults: [1×1 BayesianOptimization]
                                Alpha: [90×1 double]
                                 Bias: -0.1318
                     KernelParameters: [1×1 struct]
                                   Mu: [0.8917 0 0.6413 0.0444 0.6011 0.1159 0.5501 0.1194 0.5118 0.1813 0.4762 0.1550 0.4008 0.0934 0.3442 0.0711 0.3819 -0.0036 0.3594 -0.0240 0.3367 0.0083 0.3625 -0.0574 0.3961 -0.0712 0.5416 -0.0695 … ] (1×34 double)
                                Sigma: [0.3112 0 0.4977 0.4414 0.5199 0.4608 0.4927 0.5207 0.5071 0.4839 0.5635 0.4948 0.6222 0.4949 0.6528 0.4584 0.6180 0.4968 0.6263 0.5191 0.6098 0.5182 0.6038 0.5275 0.5785 0.5085 0.5162 0.5500 0.5759 … ] (1×34 double)
                       BoxConstraints: [351×1 double]
                      ConvergenceInfo: [1×1 struct]
                      IsSupportVector: [351×1 logical]
                               Solver: 'SMO'


  Properties, Methods

输入参数

`Tbl` — 样本数据
表

用于训练模型的样本数据，指定为表。Tbl 的每行对应一个观测值，每列对应一个预测变量。不允许多列变量和字符向量元胞数组以外的元胞数组。

（可选）Tbl 可以包含一个对应于响应变量的列和一个对应于观测值权重的列。

响应变量必须为分类数组、字符数组或字符串数组、逻辑向量或数值向量，或者字符向量元胞数组。
- fitcsvm 仅支持一类和二类（二元）分类。或者响应变量最多只能包含两个不同类，或您必须使用 ClassNames 名称-值参量指定一个或两个用于训练的类。有关多类学习的信息，请参阅 fitcecoc。
- 使用 ClassNames 名称-值参量在响应变量中指定类的顺序是很好的做法。
权重列必须为数值向量。
您必须使用 ResponseVarName 或 formula 在 Tbl 中指定响应变量，并使用 Weights 在 Tbl 中指定观测值权重。
- 通过使用 ResponseVarName 指定响应变量 - fitcsvm 将其余变量用作预测变量。要使用 Tbl 中其余变量的子集作为预测变量，请使用 PredictorNames 指定预测变量。
- 使用 formula 定义模型设定 - fitcsvm 使用 Tbl 中变量的子集作为预测变量和响应变量，如 formula 中所指定的那样。

如果 Tbl 不包含响应变量，则使用 Y 指定响应变量。响应变量 Y 的长度和 Tbl 中的行数必须相等。要使用 Tbl 中变量的子集作为预测变量，请使用 PredictorNames 指定预测变量。

数据类型: table

`ResponseVarName` — 响应变量名称
`Tbl` 中变量的名称

响应变量名称，指定为 Tbl 中变量的名称。

您必须以字符向量或字符串标量指定 ResponseVarName。例如，如果响应变量 Y 存储为 Tbl.Y，则将其指定为 "Y"。否则，软件在训练模型时会将 Tbl 的所有列（包括 Y）视为预测变量。

响应变量必须为分类数组、字符数组或字符串数组、逻辑向量或数值向量，或者字符向量元胞数组。如果 Y 是字符数组，则响应变量的每个元素必须对应于数组的一行。

使用 ClassNames 名称-值参量来指定类的顺序是很好的做法。

数据类型: char | string

`formula` — 响应变量和预测变量子集的解释模型
字符向量 | 字符串标量

由响应变量和部分预测变量构成的解释模型，指定为 "Y~x1+x2+x3" 形式的字符向量或字符串标量。在此形式中，Y 表示响应变量，x1、x2、x3 表示预测变量。

要将 Tbl 中的一部分变量指定为模型训练的预测变量，请使用公式。如果您指定公式，则软件不会使用 Tbl 中未出现在 formula 中的任何变量。

公式中的变量名称必须既是 Tbl 中的变量名称 (Tbl.Properties.VariableNames)，又是有效的 MATLAB^® 标识符。您可以使用 isvarname 函数来验证 Tbl 中的变量名称。如果变量名称无效，可以使用 matlab.lang.makeValidName 函数进行转换。

数据类型: char | string

`Y` — 类标签
分类数组 | 字符数组 | 字符串数组 | 逻辑向量 | 数值向量 | 字符向量元胞数组

用于训练 SVM 模型的类标签，指定为分类、字符或字符串数组，逻辑或数值向量，或字符向量元胞数组。

fitcsvm 仅支持一类和二类（二元）分类。或者 Y 最多只能包含两个不同类，或您必须使用 ClassNames 名称-值参量指定一个或两个用于训练的类。有关多类学习的信息，请参阅 fitcecoc。
Y 的长度和 Tbl 或 X 的行数必须相等。
如果 Y 是字符数组，则每个标签必须对应于数组的一行。
使用 ClassNames 名称-值对组参量来指定类顺序是很好的做法。

`X` — 预测变量数据
数值矩阵

用于训练 SVM 分类器的预测变量数据，指定为数值矩阵。

X 的每行对应一个观测值（也称为实例或示例），每列对应一个预测变量（也称为特征）。

Y 的长度和 X 的行数必须相等。

要按预测变量在 X 中出现的顺序指定预测变量的名称，请使用 'PredictorNames' 名称-值对组参量。

数据类型: double | single

名称-值参数

以 Name1=Value1,...,NameN=ValueN 形式指定可选参量对组，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

在 R2021a 之前，使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: fitcsvm(X,Y,'KFold',10,'Cost',[0 2;1 0],'ScoreTransform','sign') 执行 10 折交叉验证，对假正的罚分是对假负的罚分的两倍，并使用 sign 函数转换分数。

SVM 选项

`BoxConstraint` — 框约束
1 (默认) | 正标量

框约束，指定为逗号分隔的对组，其中包含 'BoxConstraint' 和一个正标量。

对于一类学习，软件始终将框约束设置为 1。

有关 BoxConstraint、Cost、Prior、Standardize 和 Weights 的关系和算法行为的详细信息，请参阅算法。

示例: 'BoxConstraint',100

数据类型: double | single

`KernelFunction` — 核函数
`'linear'` | `'gaussian'` | `'rbf'` | `'polynomial'` | 函数名称

用于计算格拉姆矩阵的元素的核函数，指定为以逗号分隔的对组，其中包含 'KernelFunction' 和核函数名称。假设 G(x_j,x_k) 是格拉姆矩阵的元素 (j,k)，其中 x_j 和 x_k 是 p 维向量，表示 X 中的观测值 j 和 k。下表说明支持的核函数名称及其函数形式。

核函数名称描述公式

核函数名称	描述	公式
`'gaussian'` 或 `'rbf'`	高斯或径向基函数 (RBF) 核，默认用于一类学习	$G (x_{j}, x_{k}) = \exp (- {‖ x_{j} - x_{k} ‖}^{2})$
`'linear'`	线性核，默认用于二类学习	$G (x_{j}, x_{k}) = x_{j}' x_{k}$
`'polynomial'`	多项式核。使用 `'PolynomialOrder',q` 指定 `q` 次多项式核。	$G (x_{j}, x_{k}) = {(1 + x_{j}' x_{k})}^{q}$

'gaussian' 或 'rbf'

高斯或径向基函数 (RBF) 核，默认用于一类学习

$G (x_{j}, x_{k}) = \exp (- {‖ x_{j} - x_{k} ‖}^{2})$

'linear'

线性核，默认用于二类学习

$G (x_{j}, x_{k}) = x_{j}' x_{k}$

'polynomial'

多项式核。使用 'PolynomialOrder',q 指定 q 次多项式核。

$G (x_{j}, x_{k}) = {(1 + x_{j}' x_{k})}^{q}$

您可以通过设置 'KernelFunction','kernel' 来设置自己的核函数，例如 kernel。值 kernel 必须采用以下形式。

function G = kernel(U,V)

其中：

U 是 m×p 矩阵。列对应于预测变量，行对应于观测值。
V 是 n×p 矩阵。列对应于预测变量，行对应于观测值。
G 是 U 和 V 行的 m×n 格拉姆矩阵。

kernel.m 必须在 MATLAB 路径上。

避免对核函数使用泛型名称是很好的做法。例如，调用 sigmoid 核函数 'mysigmoid'，而不是 'sigmoid'。

示例: 'KernelFunction','gaussian'

数据类型: char | string

`KernelScale` — 核尺度参数
`1` (默认) | `'auto'` | 正标量

核尺度参数，指定为以逗号分隔的对组，其中包含 'KernelScale' 和 'auto' 或正标量。软件将预测变量矩阵 X 的所有元素除以 KernelScale 的值。然后，软件应用适当的核范数来计算格拉姆矩阵。

如果您指定 'auto'，则软件使用启发式过程选择适当的尺度因子。这种启发式过程使用二次抽样，因此不同调用的估计值可能不同。因此，为了重现结果，请在训练前使用 rng 设置随机数种子。
如果您指定 KernelScale 和您自己的核函数，例如 'KernelFunction','kernel'，则软件会引发错误。您必须在 kernel 中应用尺度缩放。

示例: 'KernelScale','auto'

数据类型: double | single | char | string

`PolynomialOrder` — 多项式核函数阶
`3` (默认) | 正整数

多项式核函数阶，指定为以逗号分隔的对组，其中包含 'PolynomialOrder' 和正整数。

如果您设置 'PolynomialOrder' 且 KernelFunction 不是 'polynomial'，则软件会引发错误。

示例: 'PolynomialOrder',2

数据类型: double | single

`KernelOffset` — 核偏移量参数
非负标量

核偏移量参数，指定为以逗号分隔的对组，其中包含 'KernelOffset' 和一个非负标量。

软件将 KernelOffset 添加到格拉姆矩阵的每个元素。

默认值为：

0，如果求解器是 SMO（也就是说，您设置 'Solver','SMO'）
0.1，如果求解器是 ISDA（也就是说，您设置 'Solver','ISDA'）

示例: 'KernelOffset',0

数据类型: double | single

`Standardize` — 指示是否标准化预测变量数据的标志
`false` (默认) | `true`

指示是否标准化预测变量数据的标志，指定为以逗号分隔的对组，其中包含 'Standardize' 和 true (1) 或 false (0)。

如果您设置 'Standardize',true：

软件按对应的加权列均值和标准差对每个预测变量（X 或 Tbl）进行中心化并缩放。有关加权标准化的详细信息，请参阅算法。MATLAB 不对为分类预测变量生成的虚拟变量列中包含的数据进行标准化。
软件使用经过标准化的预测变量训练分类器，但会将未标准化的预测变量以矩阵或表形式存储在分类器属性 X 中。

示例: 'Standardize',true

数据类型: logical

`Solver` — 优化例程
`'ISDA'` | `'L1QP'` | `'SMO'`

优化例程，指定为以逗号分隔的对组，其中包含 'Solver' 和下表中的一个值。

值	描述
`'ISDA'`	迭代单数据算法（请参阅 [4]）
`'L1QP'`	使用 `quadprog` (Optimization Toolbox) 通过二次规划实现 L1 软边距最小化。此选项需要 Optimization Toolbox™ 许可证。有关详细信息，请参阅二次规划定义 (Optimization Toolbox)。
`'SMO'`	序列最小优化（请参阅 [2]）

对于二类学习，如果您将 'OutlierFraction' 设置为正值，则默认值为 'ISDA'；否则为 'SMO'。

示例: 'Solver','ISDA'

`Alpha` — alpha 系数的初始估计值
非负值的数值向量

alpha 系数的初始估计值，指定为以逗号分隔的对组，其中包含 'Alpha' 和非负值的数值向量。Alpha 的长度必须等于 X 的行数。

'Alpha' 的每个元素对应于 X 中的一个观测值。
'Alpha' 不能包含任何 NaN。
如果您指定 'Alpha' 和任一交叉验证名称-值对组参量（'CrossVal'、'CVPartition'、'Holdout'、'KFold' 或 'Leaveout'），软件将返回错误。

如果 Y 包含任何缺失值，则删除与缺失值对应的 Y、X 和 'Alpha' 的所有行。即，输入：

idx = ~isundefined(categorical(Y));
Y = Y(idx,:);
X = X(idx,:);
alpha = alpha(idx);

然后分别将 Y、X 和 alpha 作为响应、预测变量和初始 alpha 估计值传递。

默认值为：

0.5*ones(size(X,1),1)（用于一类学习）
zeros(size(X,1),1)（用于二类学习）

示例: 'Alpha',0.1*ones(size(X,1),1)

数据类型: double | single

`CacheSize` — 缓存大小
`1000` (默认) | `'maximal'` | 正标量

缓存大小，指定为以逗号分隔的对组，其中包含 'CacheSize' 和 'maximal' 或正标量。

如果 CacheSize 是 'maximal'，则软件预留足够的内存来容纳整个 n×n 格拉姆矩阵。

如果 CacheSize 是正标量，则软件会预留 CacheSize MB 内存用于训练模型。

示例: 'CacheSize','maximal'

数据类型: double | single | char | string

`ClipAlphas` — 指定是否限定 alpha 系数的标志
`true` (默认) | `false`

指定是否限定 alpha 系数的标志，指定为以逗号分隔的对组，其中包含 'ClipAlphas' 和 true 或 false。

假设观测值 j 的 alpha 系数是 α_j，观测值 j 的框约束是 C_j，j = 1、...、n，其中 n 是训练样本大小。

值	描述
`true`	在每次迭代中，如果 α_j 接近 0 或接近 C_j，则 MATLAB 分别将 α_j 设置为 0 或 C_j。
`false`	MATLAB 在优化过程中不更改 alpha 系数。

MATLAB 将 α 的最终值存储在经过训练的 SVM 模型对象的 Alpha 属性中。

ClipAlphas 会影响 SMO 和 ISDA 收敛。

示例: 'ClipAlphas',false

数据类型: logical

`Nu` — 用于一类学习的 ν 参数
`0.5` (默认) | 正标量

用于一类学习的 ν 参数，指定为由 'Nu' 和正标量组成的以逗号分隔的对组。Nu 必须大于 0 且最大为 1。

Nu 用于在确保大多数训练样本为正类和尽量减小分数函数权重之间进行权衡。

示例: 'Nu',0.25

数据类型: double | single

`NumPrint` — 优化诊断消息的输出间隔（迭代次数）
`1000` (默认) | 非负整数

优化诊断消息的输出间隔（迭代次数），指定为由 'NumPrint' 和非负整数组成的以逗号分隔的对组。

如果您指定 'Verbose',1 和 'NumPrint',numprint，则软件会在命令行窗口中每隔 numprint 次迭代显示来自 SMO 和 ISDA 的所有优化诊断消息。

示例: 'NumPrint',500

数据类型: double | single

`OutlierFraction` — 训练数据中离群值的预期比例
`0` (默认) | 区间 [0,1) 中的数值标量

训练数据中离群值的预期比例，指定为以逗号分隔的对组，其中包含 'OutlierFraction' 和区间 [0,1) 中的数值标量。

假设您设置 'OutlierFraction',outlierfraction，其中 outlierfraction 是大于 0 的值。

对于二类学习，软件实现稳健学习。换句话说，当优化算法收敛时，软件尝试删除 100*outlierfraction% 的观测值。删除的观测值对应于幅值较大的梯度。
对于一类学习，软件会使用合适的偏差项，使得训练集中 outlierfraction 的观测值具有负分数。

示例: 'OutlierFraction',0.01

数据类型: double | single

`RemoveDuplicates` — 指定是否用单一观测值替换重复观测值的标志
`false` (默认) | `true`

指定是否在训练数据中用单一观测值替换重复观测值的标志，指定为以逗号分隔的对组，其中包含 'RemoveDuplicates' 和 true 或 false。

如果 RemoveDuplicates 是 true，则 fitcsvm 用相同值的单一观测值替换训练数据中的重复观测值。该单一观测值的权重等于对应删除副本的权重总和（请参阅 Weights）。

提示

如果您的数据集包含许多重复的观测值，则指定 'RemoveDuplicates',true 可以大大缩短收敛时间。

数据类型: logical

`Verbose` — 详细级别
`0` (默认) | `1` | `2`

详细级别，指定为以逗号分隔的对组，其中包含 'Verbose' 和 0、1 或 2。Verbose 的值控制软件在命令行窗口中显示的优化信息量，并将这些信息作为结构体保存到 Mdl.ConvergenceInfo.History 中。

下表总结了可用的详细级别选项。

值	描述
`0`	软件不显示或保存收敛信息。
`1`	软件显示诊断消息，并每隔 `numprint` 次迭代保存收敛条件，其中 `numprint` 是名称-值对组参量 `'NumPrint'` 的值。
`2`	软件显示诊断消息，并在每次迭代时保存收敛条件。

示例: 'Verbose',1

数据类型: double | single

其他分类选项

`CategoricalPredictors` — 分类预测变量列表
正整数向量 | 逻辑向量 | 字符矩阵 | 字符串数组 | 字符向量元胞数组 | `'all'`

分类预测变量列表，指定为本表中的值之一。

值	描述
正整数向量	向量中的每个条目为一个索引值，指示对应的预测变量是分类变量。索引值介于 1 和 `p` 之间，其中 `p` 是用于训练模型的预测变量数目。如果 `fitcsvm` 使用输入变量的子集作为预测变量，则此函数仅使用此子集对预测变量进行索引。`CategoricalPredictors` 值不计算任何响应变量、观测值权重变量或函数不使用的其他变量。
逻辑向量	`true` 条目表示对应的预测变量是分类变量。向量的长度为 `p`。
字符矩阵	矩阵的每行均为预测变量的名称。名称必须与 `PredictorNames` 中的条目相匹配。系统用空格填充名称以使字符矩阵的每行具有相同的长度。
字符串数组或字符向量元胞数组	数组中的每个元素均为预测变量的名称。名称必须与 `PredictorNames` 中的条目相匹配。
`"all"`	所有预测变量均为分类预测变量。

默认情况下，如果预测变量数据在表 (Tbl) 中，并且它是逻辑向量、分类向量、字符数组、字符串数组或字符向量元胞数组，则 fitcsvm 假设变量是分类变量。如果预测变量数据是矩阵 (X)，fitcsvm 假设所有预测变量均为连续的。要将任何其他预测变量识别为分类预测变量，请使用 CategoricalPredictors 名称-值参量指定它们。

对于已识别的分类预测变量，fitcsvm 根据分类变量是无序还是有序，使用两种不同方案创建虚拟变量。对于无序分类变量，fitcsvm 为分类变量的每个水平创建一个虚拟变量。对于有序分类变量，fitcsvm 创建的虚拟变量数比类别数少一个。有关详细信息，请参阅 Automatic Creation of Dummy Variables。

示例: 'CategoricalPredictors','all'

`ClassNames` — 用于二类学习的类的名称
分类数组 | 字符数组 | 字符串数组 | 逻辑向量 | 数值向量 | 字符向量元胞数组

用于二类学习的类的名称，指定为分类、字符或字符串数组；逻辑或数值向量；或字符向量元胞数组。ClassNames 必须与 Tbl 或 Y 中的响应变量具有相同的数据类型。

如果 ClassNames 是字符数组，则每个元素必须对应于数组的一行。

使用 ClassNames 可以：

指定训练期间类的顺序。
指定对应于类顺序的任何输入或输出参量维度的顺序。例如，使用 ClassNames 指定 Cost 的维度的顺序或 predict 返回的分类分数的列顺序。
选择用于训练的类的子集。例如，假设 Y 中所有不同类名的集合是 ["a","b","c"]。要仅使用来自 "a" 和 "c" 类的观测值训练模型，请指定 ClassNames=["a","c"]。

ClassNames 的默认值为 Tbl 或 Y 中的响应变量的所有不同类名的集合。

此参量只对二类学习有效。

示例: "ClassNames",["b","g"]

`Cost` — 二类学习的误分类代价
`[0 1; 1 0]` (默认) | 方阵 | 结构体数组

二类学习的误分类代价，指定为以逗号分隔的对组，其中包括 'Cost' 和一个方阵或结构体数组。

如果您指定方阵 Cost 且观测值的真实类是 i，则 Cost(i,j) 是将一个点分类到 j 类的代价。也就是说，行对应于真实类，列对应于预测的类。要为 Cost 的对应行和列指定类顺序，则还需指定 ClassNames 名称-值对组参量。
如果您指定结构体 S，则它必须有两个字段：
- S.ClassNames，其中包含类名作为一个变量，变量的数据类型与 Y 相同。
- S.ClassificationCosts，其中包含按 S.ClassNames 中的顺序排列行和列的代价矩阵

如果您指定代价矩阵，则软件会通过合并代价矩阵中所述的用于训练的罚分来更新先验概率，并将用户指定的值存储在已训练的 SVM 模型对象的 Cost 属性中。有关 BoxConstraint、Cost、Prior、Standardize 和 Weights 的关系和算法行为的详细信息，请参阅算法。

此参量只对二类学习有效。

示例: 'Cost',[0,1;2,0]

数据类型: double | single | struct

`PredictorNames` — 预测变量名称
唯一名称的字符串数组 | 唯一字符向量元胞数组

预测变量名称，指定为唯一名称字符串数组或唯一字符向量元胞数组。PredictorNames 的功能取决于您提供训练数据的方式。

如果您提供 X 和 Y，则可以使用 PredictorNames 为 X 中的预测变量指定名称。
- PredictorNames 中名称的顺序必须对应于 X 中列的顺序。也就是说，PredictorNames{1} 是 X(:,1) 的名称，PredictorNames{2} 是 X(:,2) 的名称，依此类推。此外，size(X,2) 和 numel(PredictorNames) 必须相等。
- 默认情况下，PredictorNames 是 {'x1','x2',...}。
如果您提供 Tbl，则您可以使用 PredictorNames 来选择在训练中使用哪些预测变量。也就是说，fitcsvm 仅使用 PredictorNames 中的预测变量和训练过程中的响应变量。
- PredictorNames 必须为 Tbl.Properties.VariableNames 的子集，并且不能包含响应变量的名称。
- 默认情况下，PredictorNames 包含所有预测变量的名称。
- 最好仅使用 PredictorNames 或 formula（但不能同时使用两者）来指定训练的预测变量。

示例: "PredictorNames",["SepalLength","SepalWidth","PetalLength","PetalWidth"]

数据类型: string | cell

`Prior` — 二类学习的每个类的先验概率
`'empirical'` (默认) | `'uniform'` | 数值向量 | 结构体数组

二类学习的每个类的先验概率，指定为以逗号分隔的对组，其中包含 'Prior' 和下表中的一个值。

值	描述
`'empirical'`	类先验概率是 `Y` 中的类相对频数。
`'uniform'`	所有类先验概率等于 1/K，其中 K 是类的数目。
数值向量	向量中的每个元素均为类先验概率。根据 `Mdl.ClassNames` 对元素进行排序，或使用 `ClassNames` 名称-值对组参量指定顺序。软件对元素进行归一化，使其总和为 `1`。
结构体	具有以下两个字段的结构体 `S`： `S.ClassNames` 包含类名作为一个变量，变量的数据类型与 `Y` 相同。 `S.ClassProbs` 包含对应先验概率的向量。软件会对向量的元素进行归一化，使其总和为 `1`。

如果您指定代价矩阵，则软件将通过合并代价矩阵中所述的用于训练的罚分来更新先验概率。在将概率归一化为总和为 1 后，软件将用户指定的先验概率存储在已训练模型对象的 Prior 属性中。有关 BoxConstraint、Cost、Prior、Standardize 和 Weights 的关系和算法行为的详细信息，请参阅算法。

此参量只对二类学习有效。

示例: struct('ClassNames',{{'setosa','versicolor','virginica'}},'ClassProbs',1:3)

数据类型: char | string | double | single | struct

`ResponseName` — 响应变量名称
`"Y"` (默认) | 字符向量 | 字符串标量

响应变量名称，指定为字符向量或字符串标量。

如果您提供 Y，则您可以使用 ResponseName 来指定响应变量的名称。
如果您提供 ResponseVarName 或 formula，则您无法使用 ResponseName。

示例: ResponseName="response"

数据类型: char | string

`ScoreTransform` — 分数转换
`"none"` (默认) | `"doublelogit"` | `"invlogit"` | `"ismax"` | `"logit"` | 函数句柄 | ...

分数变换，指定为字符向量、字符串标量或函数句柄。

下表总结了可用的字符向量和字符串标量。

值	描述
`"doublelogit"`	1/(1 + e^–2x)
`"invlogit"`	log(x / (1 – x))
`"ismax"`	将分数最高的类的分数设置为 1，并将所有其他类的分数设置为 0
`"logit"`	1/(1 + e^–x)
`"none"` 或 `"identity"`	x（无变换）
`"sign"`	–1 表示 x < 0 0 表示 x = 0 1 表示 x > 0
`"symmetric"`	2x – 1
`"symmetricismax"`	将分数最高的类的分数设置为 1，并将所有其他类的分数设置为 –1
`"symmetriclogit"`	2/(1 + e^–x) – 1

对于 MATLAB 函数或您定义的函数，请使用其函数句柄进行分数变换。函数句柄必须接受矩阵（原始分数）并返回相同大小（转换后的分数）的矩阵。

示例: ScoreTransform="logit"

数据类型: char | string | function_handle

`Weights` — 观测值权重
数值向量 | `Tbl` 中变量的名称

观测值权重，指定为以逗号分隔的对组，其中包含 'Weights' 和由正值组成的数值向量或 Tbl 中变量的名称。软件使用 Weights 中的对应值对 X 或 Tbl 的每行中的观测值进行加权。Weights 的大小必须等于 X 或 Tbl 的行数。

如果您将输入数据指定为表 Tbl，则 Weights 可以是包含数值向量的 Tbl 中的变量的名称。在本例中，您必须将 Weights 指定为字符向量或字符串标量。例如，如果权重向量 W 存储为 Tbl.W，则将其指定为 'W'。否则，软件在训练模型时会将 Tbl 的所有列（包括 W）视为预测变量或响应变量。

默认情况下，Weights 是 ones(n,1)，其中 n 是 X 或 Tbl 中的观测值数目。

软件会对 Weights 进行归一化，使其总和等于对应类中的先验概率值。Inf 权重不受支持。有关 BoxConstraint、Cost、Prior、Standardize 和 Weights 的关系和算法行为的详细信息，请参阅算法。

数据类型: double | single | char | string

注意

不能将任何交叉验证名称-值参量与 OptimizeHyperparameters 名称-值参量结合使用。您只能通过使用 HyperparameterOptimizationOptions 名称-值参量来修改 OptimizeHyperparameters 的交叉验证。

交叉验证选项

`CrossVal` — 指定是否训练交叉验证分类器的标志
`'off'` (默认) | `'on'`

指定是否训练交叉验证分类器的标志，指定为以逗号分隔的对组，其中包含 'Crossval' 和 'on' 或 'off'。

如果您指定 'on'，则软件使用 10 折来训练交叉验证分类器。

您可以使用 CVPartition、Holdout、KFold 或 Leaveout 名称-值对组参量覆盖此交叉验证设置。一次只能使用一个交叉验证名称-值对组参量来创建一个交叉验证模型。

或者，稍后通过将 Mdl 传递给 crossval 来进行交叉验证。

示例: 'Crossval','on'

`CVPartition` — 交叉验证分区
`[]` (默认) | `cvpartition` 对象

交叉验证分区，指定为 cvpartition 对象，该对象指定交叉验证的类型以及训练集和验证集的索引。

要创建交叉验证模型，您只能指定以下四个名称-值参量之一：CVPartition、Holdout、KFold 或 Leaveout。

示例: 假设您使用 cvp = cvpartition(500,KFold=5) 创建一个随机分区，用于对 500 个观测值进行 5 折交叉验证。然后，您可以通过设置 CVPartition=cvp 来指定交叉验证分区。

`Holdout` — 用于留出法验证的数据比例
范围 (0,1) 内的标量值

用于留出法验证的数据比例，指定为 (0,1) 范围内的标量值。如果您指定 Holdout=p，则软件将完成以下步骤：

随机选择并预留 p*100% 的数据作为验证数据，并使用其余数据训练模型。
将紧凑的经过训练的模型存储在交叉验证模型的 Trained 属性中。

要创建交叉验证模型，您只能指定以下四个名称-值参量之一：CVPartition、Holdout、KFold 或 Leaveout。

示例: Holdout=0.1

数据类型: double | single

`KFold` — 折的数目
`10` (默认) | 大于 1 的正整数值

交叉验证模型中使用的折的数目，指定为大于 1 的正整数值。如果您指定 KFold=k，则软件将完成以下步骤：

将数据随机分为 k 个数据集。
对于每个数据集，预留用作验证数据的数据集，并使用其他 k – 1 数据集训练模型。
将 k 个经过训练的紧凑模型存储在交叉验证模型的 Trained 属性中的 k×1 元胞向量中。

要创建交叉验证模型，您只能指定以下四个名称-值参量之一：CVPartition、Holdout、KFold 或 Leaveout。

示例: KFold=5

数据类型: single | double

`Leaveout` — 留一法交叉验证标志
`"off"` (默认) | `"on"`

留一法交叉验证标志，指定为 "on" 或 "off"。如果您指定 Leaveout="on"，则对于 n 个观测值中的每一个（其中 n 是不包括缺失观测值的观测值数目，在模型的 NumObservations 属性中指定），软件完成以下步骤：

预留作为验证数据的观测值，并使用其他 n - 1 个观测值训练模型。
将 n 个紧凑的经过训练的模型存储在交叉验证模型的 Trained 属性中的 n×1 元胞向量中。

要创建交叉验证模型，您只能指定以下四个名称-值参量之一：CVPartition、Holdout、KFold 或 Leaveout。

示例: Leaveout="on"

数据类型: char | string

收敛控制选项

`DeltaGradientTolerance` — 梯度差的容差
非负标量

通过序列最小优化 (SMO) 或迭代单数据算法 (ISDA) 获得的上违反量和下违反量之间梯度差的容差，指定为由 'DeltaGradientTolerance' 和非负标量组成的以逗号分隔的对组。

如果 DeltaGradientTolerance 是 0，则软件不使用梯度差的容差来检查优化收敛。

默认值为：

如果求解器是 SMO（例如，您设置 'Solver','SMO'），默认值为 1e-3
如果求解器是 ISDA（例如，您设置 'Solver','ISDA'），默认值 0

示例: 'DeltaGradientTolerance',1e-2

数据类型: double | single

`GapTolerance` — 可行性间隙容差
`0` (默认) | 非负标量

通过 SMO 或 ISDA 获得的可行性间隙容差，指定为由 'GapTolerance' 和非负标量组成的以逗号分隔的对组。

如果 GapTolerance 是 0，则软件不使用可行性间隙容差来检查优化收敛。

示例: 'GapTolerance',1e-2

数据类型: double | single

`IterationLimit` — 数值优化迭代的最大次数
`1e6` (默认) | 正整数

数值优化迭代的最大次数，指定为以逗号分隔的对组，其中包含 'IterationLimit' 和一个正整数。

无论优化例程是否成功收敛，软件都会返回经过训练的模型。Mdl.ConvergenceInfo 包含收敛信息。

示例: 'IterationLimit',1e8

数据类型: double | single

`KKTTolerance` — 卡鲁什-库恩-塔克互补条件违规容限
非负标量

卡鲁什-库恩-塔克 (KKT) 互补条件违规容限，指定为由 'KKTTolerance' 和非负标量组成的以逗号分隔的对组。

如果 KKTTolerance 是 0，则软件不使用 KKT 互补条件违规容限来检查优化收敛。

默认值为：

如果求解器是 SMO（例如，您设置 'Solver','SMO'），默认值为 0
如果求解器是 ISDA（例如，您设置 'Solver','ISDA'），默认值 1e-3

示例: 'KKTTolerance',1e-2

数据类型: double | single

`ShrinkagePeriod` — 活动集各次归约之间的迭代次数
`0` (默认) | 非负整数

活动集各次归约之间的迭代次数，指定为由 'ShrinkagePeriod' 和非负整数组成的以逗号分隔的对组。

如果您设置 'ShrinkagePeriod',0，则软件不会缩小活动集。

示例: 'ShrinkagePeriod',1000

数据类型: double | single

超参数优化选项

`OptimizeHyperparameters` — 要针对二类学习优化的参数
`'none'` (默认) | `'auto'` | `'all'` | 合格参数名称的字符串数组或元胞数组 | `optimizableVariable` 对象的向量

要针对二类学习优化的参数，指定为以逗号分隔的对组，其中包含 'OptimizeHyperparameters' 和下列值之一：

'none' - 不优化。
'auto' - 使用 {'BoxConstraint','KernelScale','Standardize'}。
'all' - 优化所有合格参数。
合格参数名称的字符串数组或元胞数组。
optimizableVariable 对象的向量，通常是 hyperparameters 的输出。

优化尝试通过更改参数来最小化 fitcsvm 的交叉验证损失（误差）。要控制交叉验证类型和优化的其他方面，请使用 HyperparameterOptimizationOptions 名称-值参量。使用 HyperparameterOptimizationOptions 时，可以通过设置 ConstraintType 和 ConstraintBounds 选项，使用（紧凑）模型大小（而不是交叉验证损失）作为优化目标。

注意

OptimizeHyperparameters 的值会覆盖您使用其他名称-值参量指定的任何值。例如，将 OptimizeHyperparameters 设置为 "auto" 会导致 fitcsvm 优化与 "auto" 选项对应的超参数，并忽略超参数的任何指定值。

fitcsvm 的合格参数包括：

BoxConstraint - fitcsvm 在正值中搜索，默认情况下对数尺度范围为 [1e-3,1e3]。
KernelFunction - fitcsvm 在 'gaussian'、'linear' 和 'polynomial' 中搜索。
KernelScale - fitcsvm 在正值中搜索，默认情况下对数尺度范围为 [1e-3,1e3]。
PolynomialOrder - fitcsvm 在 [2,4] 范围内的整数中搜索。
Standardize - fitcsvm 在 'true' 和 'false' 中搜索。

通过传递具有非默认值的 optimizableVariable 对象的向量可设置非默认参数。例如：

load fisheriris
params = hyperparameters('fitcsvm',meas,species);
params(1).Range = [1e-4,1e6];

将 params 作为 OptimizeHyperparameters 的值传递。

默认情况下，迭代输出会出现在命令行中，绘图会根据优化中的超参数个数来显示。对于优化和绘图，目标函数是误分类率。要控制迭代输出的显示，请设置 HyperparameterOptimizationOptions 名称-值参量的 Verbose 选项。要控制绘图，请设置 HyperparameterOptimizationOptions 名称-值参量的 ShowPlots 字段。

有关示例，请参阅优化 SVM 分类器。

此参量只对二类学习有效。

示例: 'OptimizeHyperparameters','auto'

`HyperparameterOptimizationOptions` — 二类学习的优化选项
结构体

二类学习的优化选项，指定为 HyperparameterOptimizationOptions 对象或结构体。此参量修改 OptimizeHyperparameters 名称-值参量的效果。如果指定 HyperparameterOptimizationOptions，则还必须指定 OptimizeHyperparameters。所有选项均为可选项。但是，必须设置 ConstraintBounds 和 ConstraintType 才能返回 AggregateOptimizationResults。您可以在结构体中设置的选项与在 HyperparameterOptimizationOptions 对象中的选项相同，如下表中所述。

选项	值	默认值
`Optimizer`	`"bayesopt"` - 使用贝叶斯优化。在内部，此设置调用 `bayesopt`。 `"gridsearch"` - 使用每个维度的 `NumGridDivisions` 值进行网格搜索。`"gridsearch"` 基于网格的均匀无放回抽样以随机顺序进行搜索。优化后，您可以使用命令 `sortrows(Mdl.HyperparameterOptimizationResults)` 按网格顺序获得一个表。 `"randomsearch"` - 在 `MaxObjectiveEvaluations` 个点中随机搜索。	`"bayesopt"`
`ConstraintBounds`	N 优化问题的约束边界，指定为 N×2 数值矩阵或 `[]`。`ConstraintBounds` 的列包含优化问题的上界值和下界值。如果将 `ConstraintBounds` 指定为数值向量，软件会将值分配给 `ConstraintBounds` 的第二列，并将零分配给第一列。如果指定 `ConstraintBounds`，则还必须指定 `ConstraintType`。	`[]`
`ConstraintTarget`	优化问题的约束目标，指定为 `"matlab"` 或 `"coder"`。如果 `ConstraintBounds` 和 `ConstraintType` 是 `[]`，并且您设置了 `ConstraintTarget`，则软件会将 `ConstraintTarget` 设置为 `[]`。`ConstraintTarget` 和 `ConstraintType` 的值确定目标函数和约束函数。有关详细信息，请参阅 `HyperparameterOptimizationOptions`。	如果指定 `ConstraintBounds` 和 `ConstraintType`，则默认值为 `"matlab"`。否则，默认值为 `[]`。
`ConstraintType`	优化问题的约束类型，指定为 `"size"` 或 `"loss"`。如果指定 `ConstraintType`，则还必须指定 `ConstraintBounds`。`ConstraintTarget` 和 `ConstraintType` 的值确定目标函数和约束函数。有关详细信息，请参阅 `HyperparameterOptimizationOptions`。	`[]`
`AcquisitionFunctionName`	采集函数的类型： `"expected-improvement-per-second-plus"` `"expected-improvement"` `"expected-improvement-plus"` `"expected-improvement-per-second"` `"lower-confidence-bound"` `"probability-of-improvement"` 其名称包含 `per-second` 的采集函数不会产生可重现的结果，因为优化取决于目标函数的运行时间。其名称包含 `plus` 的采集函数在过度开发某个区域时会更改其行为。有关详细信息，请参阅Acquisition Function Types。	`"expected-improvement-per-second-plus"`
`MaxObjectiveEvaluations`	目标函数计算的最大数量。如果使用 `ConstraintBounds` 指定多个优化问题，则 `MaxObjectiveEvaluations` 的值将分别应用于每个优化问题。	对于 `"bayesopt"` 和 `"randomsearch"` 为 `30`，对于 `"gridsearch"` 为整个网格
`MaxTime`	优化的时间限制，指定为非负实数标量。时间限制（以秒为单位），由 `tic` 和 `toc` 测量。不管 `MaxTime` 的值如何，软件至少执行一次优化迭代。运行时间可以超过 `MaxTime`，因为 `MaxTime` 不会中断函数计算。如果使用 `ConstraintBounds` 指定多个优化问题，时间限制将分别应用于每个优化问题。	`Inf`
`NumGridDivisions`	用于 `Optimizer="gridsearch"`，表示每个维度中的值的数量。该值可以是由指定每个维度上值个数的正整数组成的向量，也可以是应用于所有维度的标量。对于分类变量，软件会忽略此选项。	`10`
`ShowPlots`	指示是否显示优化进度图的逻辑值。如果此选项为 `true`，则软件绘制最佳观测目标函数值对迭代编号的图。如果使用贝叶斯优化 (`Optimizer="bayesopt"`)，软件还会绘制最佳估计目标函数值。最佳观测目标函数值和最佳估计目标函数值分别对应于迭代输出的 `BestSoFar (observed)` 和 `BestSoFar (estim.)` 列中的值。您可以在 `Mdl.HyperparameterOptimizationResults` 的属性 `ObjectiveMinimumTrace` 和 `EstimatedObjectiveMinimumTrace` 中找到这些值。如果问题包含一个或两个用于贝叶斯优化的优化参数，则 `ShowPlots` 还会绘制目标函数的模型对这些参数的图。	`true`
`SaveIntermediateResults`	指示是否保存优化结果的逻辑值。如果此选项为 `true`，则软件会在每次迭代中覆盖名为 `"BayesoptResults"` 的工作区变量。变量是 `BayesianOptimization` 对象。如果使用 `ConstraintBounds` 指定多个优化问题，则工作区变量是名为 `"AggregateBayesoptResults"` 的 `AggregateBayesianOptimization` 对象。	`false`
`Verbose`	在命令行中的显示级别： `0` - 不显示迭代输出 `1` - 显示迭代输出 `2` - 显示带额外信息的迭代输出有关详细信息，请参阅 `bayesopt` `Verbose` 名称-值参量和示例使用贝叶斯优化来优化分类器拟合。	`1`
`UseParallel`	指示是否并行运行贝叶斯优化的逻辑值（并行运行贝叶斯优化需要 Parallel Computing Toolbox™）。由于并行时序的不可再现性，并行贝叶斯优化不一定产生可重现的结果。有关详细信息，请参阅 Parallel Bayesian Optimization。	`false`
`Repartition`	逻辑值，指示是否在每次迭代时对交叉验证进行重新分区。如果此选项为 `false`，优化器将使用单个分区进行优化。值 `true` 通常可得到最稳健的结果，因为此设置考虑分区噪声。然而，为了获得最优结果，设置为 `true` 后函数计算次数至少会翻一倍。	`false`
仅指定以下三个选项之一。
`CVPartition`	`cvpartition` 对象，由 `cvpartition` 创建	如果未指定交叉验证选项，则为 `KFold=5`
`Holdout`	`(0,1)` 范围内的标量，表示保留比例
`KFold`	大于 1 的整数

此参量只对二类学习有效。

示例: 'HyperparameterOptimizationOptions',struct('MaxObjectiveEvaluations',60)

数据类型: struct

输出参量

`Mdl` — 经过训练的 SVM 分类模型
`ClassificationSVM` 模型对象 | `ClassificationPartitionedModel` 交叉验证模型对象

经过训练的 SVM 分类模型，以 ClassificationSVM 模型对象或 ClassificationPartitionedModel 交叉验证模型对象形式返回。

如果您设置任一名称-值对组参量 KFold、Holdout、Leaveout、CrossVal 或 CVPartition，则 Mdl 是 ClassificationPartitionedModel 交叉验证模型对象。否则，Mdl 为 ClassificationSVM 模型对象。

要引用 Mdl 的属性，请使用圆点表示法。例如，在命令行窗口中输入 Mdl.Alpha 以显示经过训练的拉格朗日乘数。

如果指定 OptimizeHyperparameters 并设置 HyperparameterOptimizationOptions 的 ConstraintType 和 ConstraintBounds 选项，则 Mdl 是由模型对象组成的 N×1 元胞数组，其中 N 等于 ConstraintBounds 中的行数。如果优化问题都未产生可行的模型，则每个元胞数组值为 []。

`AggregateOptimizationResults` — 聚合优化结果
`AggregateBayesianOptimization` 对象

聚合多个优化问题的优化结果，以 AggregateBayesianOptimization 对象形式返回。要返回 AggregateOptimizationResults，必须指定 OptimizeHyperparameters 和 HyperparameterOptimizationOptions。您还必须指定 HyperparameterOptimizationOptions 的 ConstraintType 和 ConstraintBounds 选项。有关说明如何生成此输出的示例，请参阅Hyperparameter Optimization with Multiple Constraint Bounds。

限制

fitcsvm 为一类或二类学习应用训练 SVM 分类器。要使用就有两个以上类的数据训练 SVM 分类器，请使用 fitcecoc。
fitcsvm 支持低维和中维数据集。对于高维数据集，请改用 fitclinear。

详细信息

框约束

框约束是参数，它控制对违反边距的观测值施加的最大罚分，这有助于防止过拟合（正则化）。

如果增加框约束，则 SVM 分类器分配的支持向量会更少。然而，增加框约束会导致更长的训练时间。

格拉姆矩阵

由 n 个向量 {x₁,..,x_n; x_j ∊ R^p} 组成的格拉姆矩阵是一个 n×n 矩阵，其中元素 (j,k) 定义为 G(x_j,x_k) = <ϕ(x_j),ϕ(x_k)>，即使用核函数 ϕ 的变换后的预测变量的内积。

对于非线性 SVM，算法使用预测变量数据 X 的行形成格拉姆矩阵。对偶问题形式用生成的格拉姆矩阵的对应元素替换 X 中观测值的内积（称为“核方法”）。因此，非线性 SVM 在变换后的预测变量空间中运算以找到分离超平面。

卡鲁什-库恩-塔克 (KKT) 互补条件

KKT 互补条件是最优非线性规划解所需的优化约束。

在 SVM 中，对于所有 j = 1、...、n，KKT 互补条件是

${\begin{cases} α_{j} [y_{j} f (x_{j}) - 1 + ξ_{j}] = 0 \\ ξ_{j} (C - α_{j}) = 0 \end{cases}$

，其中 $f (x_{j}) = ϕ (x_{j})' β + b,$ ϕ 是核函数（请参阅格拉姆矩阵），ξ_j 是松弛变量。如果这些类完全可分离，则对于所有 j = 1,...,n，满足 ξ_j = 0。

一类学习

一类学习，或无监督 SVM，旨在从高维预测变量空间（而不是原始预测变量空间）的原点分离数据，是一种用于离群值检测的算法。

该算法类似于二类分类的 SVM 的算法。目标是最小化关于 $α_{1}, ..., α_{n}$ 的对偶表达式

$0.5 \sum_{j k} α_{j} α_{k} G (x_{j}, x_{k})$

，且对于所有 j = 1、...、n，满足

$\sum α_{j} = n ν$

和 $0 \leq α_{j} \leq 1$ 。G(x_j,x_k) 的值在格拉姆矩阵的元素 (j,k) 中。

较小的 ν 值会导致较少支持向量，因此决策边界平滑、粗糙。较大的 ν 值会导致较多支持向量，因此决策边界弯曲、灵活。最佳 ν 值应足够大以体现数据的复杂性，同时足够小以避免过度训练。此外，0 < ν ≤ 1。

有关详细信息，请参阅[5]。

支持向量

支持向量是与 α₁,...,α_n 的严格正估计值对应的观测值。

对于给定训练集，最好选用产生较少支持向量的 SVM 分类器。

用于二类分类的支持向量机

SVM 二类分类算法搜索将数据分成两类的最优超平面。对于可分离类，最优超平面会最大化自身周围的边距（不包含任何观测值的空间），从而在正类和负类间创建边界。对于不可分离的类，目标是相同的，但是，如果有观测值位于其类边界的错误一侧，则算法会相应地对边距长度施加罚分。

线性 SVM 分数函数是

$f (x) = x' β + b,$

其中：

x 是观测值（对应于 X 的一行）。
向量 β 包含定义超平面的正交向量的系数（对应于 Mdl.Beta）。对于可分离的数据，最佳边距长度是 $2 / ‖ β ‖ .$
b 是偏差项（对应于 Mdl.Bias）。

特定系数的 f(x) 的根定义超平面。对于特定的超平面，f(z) 是从 z 点到超平面的距离。

算法搜索最大边距长度，同时将观测值分为正类 (y = 1) 和负类 (y = –1)。

对于可分离的类，目标是最小化关于 β 和 b 的 $‖ β ‖$ ，并且对于所有 j = 1、...、n，满足 y_jf(x_j) ≥ 1。这是针对可分离类的原问题形式。
对于不可分离的类，算法会在遇到跨越类边界的观测值时使用松弛变量 (ξ_j) 对目标函数进行罚分。对于未跨越类边界的观测值，ξ_j = 0，否则 ξ_j ≥ 0。
目标是最小化关于 β、b 和 ξ_j 的 $0.5 {‖ β ‖}^{2} + C \sum ξ_{j}$ ，对于所有 j = 1,..,n 和正标量框约束 C，满足 $y_{j} f (x_{j}) \geq 1 - ξ_{j}$ 和 $ξ_{j} \geq 0$ 。这是针对不可分离类的原问题形式。

算法采用拉格朗日乘数方法优化目标，引入 n 个系数 α₁,...,α_n（对应于 Mdl.Alpha）。线性 SVM 的对偶问题形式如下：

对于可分离的类，最小化关于 α₁,...,α_n 的

$0.5 \sum_{j = 1}^{n} \sum_{k = 1}^{n} α_{j} α_{k} y_{j} y_{k} x_{j}' x_{k} - \sum_{j = 1}^{n} α_{j}$
，对于所有 j = 1,...,n，满足 $\sum α_{j} y_{j} = 0$ ，α_j ≥ 0，且满足卡鲁什-库恩-塔克 (KKT) 互补条件。
对于不可分离的类，目标与可分离的类相同，不同之处是所有 j = 1、...、n 需满足附加条件 $0 \leq α_{j} \leq C$ 。

得到的分数函数是

$\hat{f} (x) = \sum_{j = 1}^{n} {\hat{α}}_{j} y_{j} x' x_{j} + \hat{b} .$

$\hat{b}$ 是偏差的估计值， ${\hat{α}}_{j}$ 是向量 $\hat{α}$ 的第 j 个估计值，j = 1,...,n。写为这种形式时，score 函数不再需要原问题形式中的 β 估计值。

SVM 算法使用 $sign (\hat{f} (z)) .$ 对新观测值 z 进行分类

在某些情况下，非线性边界对类进行分隔。非线性 SVM 在经过变换的预测变量空间中计算以找到最佳的分离超平面。

非线性 SVM 的对偶问题可表示为关于 α₁、...、α_n 的以下形式

$0.5 \sum_{j = 1}^{n} \sum_{k = 1}^{n} α_{j} α_{k} y_{j} y_{k} G (x_{j}, x_{k}) - \sum_{j = 1}^{n} α_{j}$

对于所有 j = 1、..、n，满足 $\sum α_{j} y_{j} = 0$ ， $0 \leq α_{j} \leq C$ ，且满足 KKT 互补条件。G(x_k,x_j) 是格拉姆矩阵的元素。得到的分数函数是

$\hat{f} (x) = \sum_{j = 1}^{n} {\hat{α}}_{j} y_{j} G (x, x_{j}) + \hat{b} .$

有关详细信息，请参阅了解支持向量机、[1] 和 [3]。

提示

除非您的数据集很大，否则请始终尝试标准化预测变量（请参阅 Standardize）。标准化可使预测变量不受其测量尺度的影响。
使用 KFold 名称-值对组参量进行交叉验证是很好的做法。交叉验证结果决定 SVM 分类器的泛化能力。
对于一类学习：
- 名称-值对组参量 Alpha 的默认设置可能导致较长的训练时间。要加快训练速度，可将 Alpha 设置为主要由 0 组成的向量。
- 将名称-值对组参量 Nu 设置为更接近 0 的值可产生更少的支持向量，从而获得更平滑但粗糙的决策边界。
支持向量中的稀疏性是 SVM 分类器的一个理想属性。要减少支持向量的数量，可将 BoxConstraint 设置为较大的值。此操作会增加训练时间。
为了获得最佳训练时间，请将 CacheSize 设置为计算机允许的最大内存限制。
如果您期望支持向量比训练集中的观测值少得多，则您可以使用名称-值对组参量 'ShrinkagePeriod' 缩小活动集，从而显著加快收敛速度。指定 'ShrinkagePeriod',1000 是很好的做法。
远离决策边界的重复观测值不影响收敛。然而，决策边界附近出现的少数几个重复的观测值可能会大幅减慢收敛速度。在以下情况下，要加快收敛速度，请指定 'RemoveDuplicates',true：
- 您的数据集包含许多重复的观测值。
- 您怀疑有几个重复的观测值接近决策边界。
要在训练期间保留原始数据集，fitcsvm 必须临时分别存储两个数据集：原始数据集和没有重复观测值的数据集。因此，如果您为包含少量重复观测值的数据集指定 true，则 fitcsvm 消耗的内存将接近原始数据的两倍。
在训练模型后，您可以生成预测新数据标签的 C/C++ 代码。生成 C/C++ 代码需要 MATLAB Coder™。有关详细信息，请参阅Introduction to Code Generation。

算法

有关 SVM 二类分类算法的数学公式，请参阅用于二类分类的支持向量机和了解支持向量机。
NaN、<undefined>、空字符向量 ('')、空字符串 ("") 和 <missing> 值表示缺失值。fitcsvm 会删除对应于缺失响应的整行数据。在计算总权重时（请参阅下几项内容），如果某权重所对应的观测值至少具有一个缺失变量，则 fitcsvm 忽略该权重。此操作会导致平衡类问题中出现不平衡的先验概率。因此，观测值框约束可能不等于 BoxConstraint。
如果您指定 Cost、Prior 和 Weights 名称-值参量，则输出模型对象会将指定的值分别存储在 Cost、Prior 和 W 属性中。Cost 属性存储用户指定的代价矩阵 (C)，无需进行任何修改。Prior 和 W 属性分别存储归一化后的先验概率和观测值权重。对于模型训练，软件会更新先验概率和观测值权重，以纳入代价矩阵中所述的罚分。有关详细信息，请参阅Misclassification Cost Matrix, Prior Probabilities, and Observation Weights。
请注意，Cost 和 Prior 名称-值参量用于二类学习。对于一类学习，Cost 和 Prior 属性分别存储 0 和 1。
对于二类学习，fitcsvm 为训练数据中的每个观测值指定一个框约束。观测值 j 的框约束的公式是

$C_{j} = n C_{0} w_{j}^{*},$
，其中 C₀ 是初始框约束（请参阅 BoxConstraint 名称-值参量），而 w_j^* 是观测值 j 的由 Cost 和 Prior 调整的观测值权重。有关观测值权重的详细信息，请参阅Adjust Prior Probabilities and Observation Weights for Misclassification Cost Matrix。
如果您将 Standardize 指定为 true 并设置 Cost、Prior 或 Weights 名称-值参量，则 fitcsvm 会使用对应于预测变量的加权均值和加权标准差对预测变量进行标准化。也就是说，fitcsvm 使用

$x_{j}^{*} = \frac{x_{j} - μ_{j}^{*}}{σ_{j}^{*}},$
标准化预测变量 j（x_j，其中 x_jk 是预测变量 j（列）的观测值 k（行），且

$\begin{matrix} μ_{j}^{*} = \frac{1}{\sum_{k} w_{k}^{*}} \sum_{k} w_{k}^{*} x_{j k}, \\ {(σ_{j}^{*})}^{2} = \frac{v_{1}}{v_{1}^{2} - v_{2}} \sum_{k} w_{k}^{*} {(x_{j k} - μ_{j}^{*})}^{2}, \\ v_{1} = \sum_{j} w_{j}^{*}, \\ v_{2} = \sum_{j} {(w_{j}^{*})}^{2} . \end{matrix}$
假设 p 是您预期在训练数据中的离群值比例，并且您设置了 'OutlierFraction',p。
- 对于一类学习，软件会训练偏差项，使得训练数据中 100p% 的观测值具有负分数。
- 对于二类学习，软件会实施稳健学习。换句话说，当优化算法收敛时，软件会尝试删除 100p% 的观测值。删除的观测值对应于幅值较大的梯度。
如果预测变量数据包含分类变量，则软件通常会对这些变量进行完全虚拟变量编码。软件为每个分类变量的每个水平创建一个虚拟变量。
- PredictorNames 属性为每个原始预测变量名称存储一个元素。例如，假设有三个预测变量，其中一个是具有三个水平的分类变量。那么 PredictorNames 是 1×3 个字符向量元胞数组，其中包含预测变量的原始名称。
- ExpandedPredictorNames 属性为每个预测变量（包括虚拟变量）存储一个元素。例如，假设有三个预测变量，其中一个是具有三个水平的分类变量。那么 ExpandedPredictorNames 就是 1×5 字符向量数组，其中包含预测变量和新虚拟变量的名称。
- 同样，Beta 属性为每个预测变量（包括虚拟变量）存储一个 beta 系数。
- SupportVectors 属性存储支持向量的预测变量值，包括虚拟变量。例如，假设有 m 个支持向量和三个预测变量，其中一个预测变量是具有三个水平的分类变量。那么 SupportVectors 就是 n×5 矩阵。
- X 属性将训练数据存储为原始输入，不包括虚拟变量。当输入为表时，X 仅包含用作预测变量的列。
对于表中指定的预测变量，如果任何变量包含经过排序的（有序）类别，软件会对这些变量使用有序编码。
- 对于具有 k 个有序水平的变量，软件会创建 k – 1 个虚拟变量。在第 j 个虚拟变量中，前 j 个水平的对应值为 –1；从 j + 1 至 k 的水平的对应值为 +1。
- 存储在 ExpandedPredictorNames 属性中的虚拟变量的名称使用值 +1 指示第一个水平。软件会为虚拟变量另外存储 k – 1 个预测变量名称，包括水平 2、3、...、k 的名称。
所有求解器都实现 L1 软边距最小化算法。
对于一类学习，软件估计拉格朗日乘数 α₁、...、α_n，满足

$\sum_{j = 1}^{n} α_{j} = n ν .$

替代功能

您还可以使用 ocsvm 函数来训练用于异常检测的一类 SVM 模型。

与 fitcsvm 函数相比，ocsvm 函数针对异常检测提供的首选工作流更简单。
- ocsvm 函数返回 OneClassSVM 对象、异常指标和异常分数。您可以使用输出来识别训练数据中的异常。要找出新数据中的异常，可以使用 OneClassSVM 的 isanomaly 对象函数。isanomaly 函数返回新数据的异常指标和分数。
- fitcsvm 函数支持一类和二类分类。如果类标签变量只包含一个类（例如，由 1 组成的向量），fitcsvm 会训练一类分类模型并返回 ClassificationSVM 对象。要识别异常，您必须首先使用 ClassificationSVM 的 resubPredict 或 predict 对象函数计算异常分数，然后通过找出具有负分数的观测值来识别异常。
- 请注意，大的正异常分数表示 ocsvm 中存在异常，而负分数表示 ClassificationSVM 的 predict 中存在异常。
ocsvm 函数基于 SVM 的原问题形式找到决策边界，而 fitcsvm 函数基于 SVM 的对偶问题形式找到决策边界。
对于大型数据集（大型 n），ocsvm 中求解器的计算开销低于 fitcsvm 中的求解器。与 fitcsvm 中需要计算 n×n格拉姆矩阵的求解器不同，ocsvm 中的求解器只需形成大小为 n×m 的矩阵。此处，m 是扩展空间的维数，对于大数据来说，此维数通常远远小于 n。

参考

[1] Christianini, N., and J. C. Shawe-Taylor. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge, UK: Cambridge University Press, 2000.

[2] Fan, R.-E., P.-H. Chen, and C.-J. Lin. “Working set selection using second order information for training support vector machines.” Journal of Machine Learning Research, Vol. 6, 2005, pp. 1889–1918.

[3] Hastie, T., R. Tibshirani, and J. Friedman. The Elements of Statistical Learning, Second Edition. NY: Springer, 2008.

[4] Kecman V., T. -M. Huang, and M. Vogt. “Iterative Single Data Algorithm for Training Kernel Machines from Huge Data Sets: Theory and Performance.” Support Vector Machines: Theory and Applications. Edited by Lipo Wang, 255–274. Berlin: Springer-Verlag, 2005.

[5] Scholkopf, B., J. C. Platt, J. C. Shawe-Taylor, A. J. Smola, and R. C. Williamson. “Estimating the Support of a High-Dimensional Distribution.” Neural Comput., Vol. 13, Number 7, 2001, pp. 1443–1471.

[6] Scholkopf, B., and A. Smola. Learning with Kernels: Support Vector Machines, Regularization, Optimization and Beyond, Adaptive Computation and Machine Learning. Cambridge, MA: The MIT Press, 2002.

扩展功能

自动并行支持
通过使用 Parallel Computing Toolbox™ 自动运行并行计算来加快代码执行。

要执行并行超参数优化，请在调用 fitcsvm 函数时使用 HyperparameterOptimizationOptions 名称-值参量中的 UseParallel=true 选项。

有关并行超参数优化的详细信息，请参阅 Parallel Bayesian Optimization。

有关并行计算的一般信息，请参阅使用自动并行支持运行 MATLAB 函数 (Parallel Computing Toolbox)。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

用法说明和限制：

不支持一类分类。标签必须包含两个不同类。
您无法将 KernelFunction 名称-值参量指定为自定义核函数。
您只能将 Solver 名称-值参量指定为 "SMO"。
您无法指定 OutlierFraction 或 ShrinkagePeriod 名称-值参量。
预测变量数据不能包含无限值。
如果满足以下任一条件，则 fitcsvm 在 GPU 上进行模型拟合：
- 输入参量 X 是 gpuArray 对象。
- 输入参量 Tbl 包含 gpuArray 预测变量。

有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2014a 中推出