Main Content

edge

Classification edge for generalized additive model (GAM)

Since R2021a

collapse all in page

    Syntax

    e = edge(Mdl,Tbl,ResponseVarName)
    e = edge(Mdl,Tbl,Y)
    e = edge(Mdl,X,Y)
    e = edge(___,Name,Value)

    Description

    e = edge(Mdl,Tbl,ResponseVarName) returns the Classification Edge (e) for the generalized additive model Mdl using the predictor data in Tbl and the true class labels in Tbl.ResponseVarName.

    e = edge(Mdl,Tbl,Y) uses the predictor data in table Tbl and the true class labels in Y.

    e = edge(Mdl,X,Y) uses the predictor data in matrix X and the true class labels in Y.

    example

    e = edge(___,Name,Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in previous syntaxes. For example, you can specify observation weights and whether to include interaction terms in computations.

    example

    Examples

    collapse all

    Open Live Script

    Estimate the test sample classification margins and edge of a generalized additive model. The test sample margins are the observed true class scores minus the false class scores, and the test sample edge is the mean of the margins.

    Load the fisheriris data set. Create X as a numeric matrix that contains two sepal and two petal measurements for versicolor and virginica irises. Create Y as a cell array of character vectors that contains the corresponding iris species.

    load fisheriris
inds = strcmp(species,'versicolor') | strcmp(species,'virginica');
X = meas(inds,:);
Y = species(inds,:);

    Randomly partition observations into a training set and a test set with stratification, using the class information in Y. Specify a 30% holdout sample for testing.

    rng('default') % For reproducibility
cv = cvpartition(Y,'HoldOut',0.30);

    Extract the training and test indices.

    trainInds = training(cv);
testInds = test(cv);

    Specify the training and test data sets.

    XTrain = X(trainInds,:);
YTrain = Y(trainInds);
XTest = X(testInds,:);
YTest = Y(testInds);

    Train a GAM using the predictors XTrain and class labels YTrain. A recommended practice is to specify the class names.

    Mdl = fitcgam(XTrain,YTrain,'ClassNames',{'versicolor','virginica'});

    Mdl is a ClassificationGAM model object.

    Estimate the test sample classification margins and edge.

    m = margin(Mdl,XTest,YTest);
e = edge(Mdl,XTest,YTest)
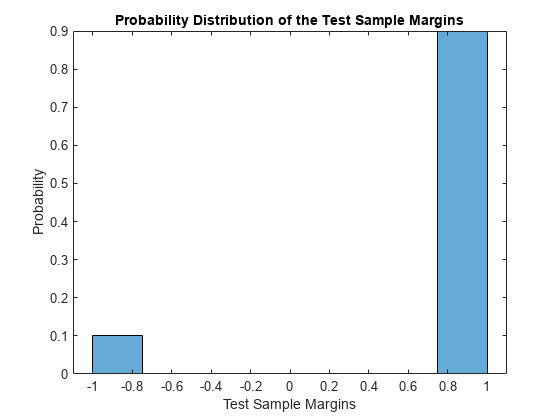
    e = 
0.8000

    Display the histogram of the test sample classification margins.

    histogram(m,length(unique(m)),'Normalization','probability')
xlabel('Test Sample Margins')
ylabel('Probability')
title('Probability Distribution of the Test Sample Margins')

    Figure contains an axes object. The axes object with title Probability Distribution of the Test Sample Margins, xlabel Test Sample Margins, ylabel Probability contains an object of type histogram.

    Open Live Script

    Estimate the test sample weighted edge (the weighted average of margins) of a generalized additive model.

    Load the fisheriris data set. Create X as a numeric matrix that contains two sepal and two petal measurements for versicolor and virginica irises. Create Y as a cell array of character vectors that contains the corresponding iris species.

    load fisheriris
idx1 = strcmp(species,'versicolor') | strcmp(species,'virginica');
X = meas(idx1,:);
Y = species(idx1,:);

    Suppose that the quality of some measurements is lower because they were measured with older technology. To simulate this effect, add noise to a random subset of 20 measurements.

    rng('default') % For reproducibility
idx2 = randperm(size(X,1),20);
X(idx2,:) = X(idx2,:) + 2*randn(20,size(X,2));

    Randomly partition observations into a training set and a test set with stratification, using the class information in Y. Specify a 30% holdout sample for testing.

    cv = cvpartition(Y,'HoldOut',0.30);

    Extract the training and test indices.

    trainInds = training(cv);
testInds = test(cv);

    Specify the training and test data sets.

    XTrain = X(trainInds,:);
YTrain = Y(trainInds);
XTest = X(testInds,:);
YTest = Y(testInds);

    Train a GAM using the predictors XTrain and class labels YTrain. A recommended practice is to specify the class names.

    Mdl = fitcgam(XTrain,YTrain,'ClassNames',{'versicolor','virginica'});

    Mdl is a ClassificationGAM model object.

    Estimate the test sample edge.

    e = edge(Mdl,XTest,YTest)
    e = 
0.8000

    The average margin is approximately 0.80.

    One way to reduce the effect of the noisy measurements is to assign them less weight than the other observations. Define a weight vector that gives the higher quality observations twice the weight of the other observations.

    n = size(X,1);
weights = ones(size(X,1),1);
weights(idx2) = 0.5;
weightsTrain = weights(trainInds);
weightsTest = weights(testInds);

    Train a GAM using the predictors XTrain, class labels YTrain, and weights weightsTrain.

    Mdl_W = fitcgam(XTrain,YTrain,'Weights',weightsTrain,...
    'ClassNames',{'versicolor','virginica'});

    Estimate the test sample weighted edge using the weighting scheme.

    e_W = edge(Mdl_W,XTest,YTest,'Weights',weightsTest)
    e_W = 
0.8770

    The weighted average margin is approximately 0.88. This result indicates that, on average, the labels from weighted classifier labels have higher confidence.

    Open Live Script

    Compare a GAM with linear terms to a GAM with both linear and interaction terms by examining the test sample margins and edge. Based solely on this comparison, the classifier with the highest margins and edge is the best model.

    Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, either bad ('b') or good ('g').

    load ionosphere

    Randomly partition observations into a training set and a test set with stratification, using the class information in Y. Specify a 30% holdout sample for testing.

    rng('default') % For reproducibility
cv = cvpartition(Y,'Holdout',0.30);

    Extract the training and test indices.

    trainInds = training(cv);
testInds = test(cv);

    Specify the training and test data sets.

    XTrain = X(trainInds,:);
YTrain = Y(trainInds);
XTest = X(testInds,:);
YTest = Y(testInds);

    Train a GAM that contains both linear and interaction terms for predictors. Specify to include all available interaction terms whose p-values are not greater than 0.05.

    Mdl = fitcgam(XTrain,YTrain,'Interactions','all','MaxPValue',0.05)
    Mdl = 
  ClassificationGAM
             ResponseName: 'Y'
    CategoricalPredictors: []
               ClassNames: {'b'  'g'}
           ScoreTransform: 'logit'
                Intercept: 3.0398
             Interactions: [561x2 double]
          NumObservations: 246

    Mdl is a ClassificationGAM model object. Mdl includes all available interaction terms.

    Estimate the test sample margins and edge for Mdl. 

    M = margin(Mdl,XTest,YTest);
E = edge(Mdl,XTest,YTest)
    E = 
0.7848

    Estimate the test sample margins and edge for Mdl without including interaction terms.

    M_nointeractions = margin(Mdl,XTest,YTest,'IncludeInteractions',false);
E_nointeractions = edge(Mdl,XTest,YTest,'IncludeInteractions',false)
    E_nointeractions = 
0.7871

    Display the distributions of the margins using box plots.

    boxplot([M M_nointeractions],'Labels',{'Linear and Interaction Terms','Linear Terms Only'})
title('Box Plots of Test Sample Margins')

    Figure contains an axes object. The axes object with title Box Plots of Test Sample Margins contains 14 objects of type line. One or more of the lines displays its values using only markers

    The margins M and M_nointeractions have a similar distribution, but the test sample edge of the classifier with only linear terms is larger. Classifiers that yield relatively large margins are preferred.

    Input Arguments

    collapse all

    Generalized additive model, specified as a ClassificationGAM or CompactClassificationGAM model object.

    • If you trained Mdl using sample data contained in a table, then the input data for edge must also be in a table (Tbl).

    • If you trained Mdl using sample data contained in a matrix, then the input data for edge must also be in a matrix (X).

    Sample data, specified as a table. Each row of Tbl corresponds to one observation, and each column corresponds to one predictor variable. Multicolumn variables and cell arrays other than cell arrays of character vectors are not allowed.

    Tbl must contain all the predictors used to train Mdl. Optionally, Tbl can contain a column for the response variable and a column for the observation weights.

    • The response variable must have the same data type as Mdl.Y. (The software treats string arrays as cell arrays of character vectors.) If the response variable in Tbl has the same name as the response variable used to train Mdl, then you do not need to specify ResponseVarName.

    • The weight values must be a numeric vector. You must specify the observation weights in Tbl by using 'Weights'.

    If you trained Mdl using sample data contained in a table, then the input data for edge must also be in a table.

    Data Types: table

    Response variable name, specified as a character vector or string scalar containing the name of the response variable in Tbl. For example, if the response variable Y is stored in Tbl.Y, then specify it as 'Y'.

    Data Types: char | string

    Class labels, specified as a categorical, character, or string array, a logical or numeric vector, or a cell array of character vectors. Each row of Y represents the classification of the corresponding row of X or Tbl.

    Y must have the same data type as Mdl.Y. (The software treats string arrays as cell arrays of character vectors.)

    Data Types: single | double | categorical | logical | char | string | cell

    Predictor data, specified as a numeric matrix. Each row of X corresponds to one observation, and each column corresponds to one predictor variable.

    If you trained Mdl using sample data contained in a matrix, then the input data for edge must also be in a matrix.

    Data Types: single | double

    Name-Value Arguments

    Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

    Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

    Example: 'IncludeInteractions',false,'Weights',w specifies to exclude interaction terms from the model and to use the observation weights w.

    Flag to include interaction terms of the model, specified as true or false.

    The default 'IncludeInteractions' value is true if Mdl contains interaction terms. The value must be false if the model does not contain interaction terms.

    Example: 'IncludeInteractions',false

    Data Types: logical

    Observation weights, specified as a vector of scalar values or the name of a variable in Tbl. The software weights the observations in each row of X or Tbl with the corresponding value in Weights. The size of Weights must equal the number of rows in X or Tbl.

    If you specify the input data as a table Tbl, then Weights can be the name of a variable in Tbl that contains a numeric vector. In this case, you must specify Weights as a character vector or string scalar. For example, if the weights vector W is stored in Tbl.W, then specify it as 'W'.

    edge normalizes the weights in each class to add up to the value of the prior probability of the respective class.

    Data Types: single | double | char | string

    More About

    collapse all

    Classification Edge

    The classification edge is the weighted mean of the classification margins.

    One way to choose among multiple classifiers, for example to perform feature selection, is to choose the classifier that yields the greatest edge.

    Classification Margin

    The classification margin for binary classification is, for each observation, the difference between the classification score for the true class and the classification score for the false class.

    If the margins are on the same scale (that is, the score values are based on the same score transformation), then they serve as a classification confidence measure. Among multiple classifiers, those that yield greater margins are better.

    Version History

    Introduced in R2021a

    See Also

    | | |

    Topics