聚类分析
此示例说明如何使用 Statistics and Machine Learning Toolbox™ 中的聚类分析来检查观测值或对象的相似性和相异性。数据通常可以自然划分到观测值组或簇中,同一簇中对象的特性是相似的,不同簇中对象的特性是相异的。
K 均值和层次聚类
Statistics and Machine Learning Toolbox 中的一些函数可执行 K 均值聚类和层次聚类。
K 均值聚类是一种分区方法,它将数据中的观测值视为具有位置和相互间距离的对象。它将对象划分为 K 个互斥簇,使每个簇中的对象尽可能彼此靠近,并尽可能远离其他簇中的对象。每个簇的特性由其质心或中心点决定。当然,聚类中使用的距离通常不代表空间距离。
层次聚类是通过创建聚类树,同时在多个距离尺度内调查数据分组的一种方法。与 K-均值法不同,树并不是一组簇的简单组合,而是一个多级层次结构,较低级别的簇在相邻的更高级别合并成新的簇。使用这种方法,您可以选择最适合您的应用场景的聚类尺度或级别。
此示例中使用的一些函数调用 MATLAB® 内置随机数生成函数。要得到与此示例完全相同的结果,请执行以下命令,将随机数生成器设置为已知状态。如果您不设置状态,结果可能会略有不同,例如,簇可能会以不同的顺序编号。另外,有可能产生次优聚类解(本示例也讨论了次优解,以及避免次优解的方法)。
rng(6,'twister')
Fisher 鸢尾花数据
20 世纪 20 年代,植物学家收集了 150 个鸢尾花标本(三个品种各取 50 个标本)的萼片长度、萼片宽度、花瓣长度和花瓣宽度的测量值。这些测量值被称为 Fisher 鸢尾花数据集。
在此数据集中,每个观测值都来自一个已知的品种,因此已经有明显的方法对数据进行分组。现在,我们将忽略品种信息,仅使用原始测量值对数据进行聚类。完成后,我们可以将得到的簇与实际的品种进行比较,以了解这三种鸢尾花是否具有不同的特性。
使用 K 均值聚类方法对 Fisher 鸢尾花数据进行聚类
函数 kmeans 使用迭代算法执行 K 均值聚类,该算法将对象分配给簇,使每个对象到其所在簇质心的距离之和最小。对 Fisher 鸢尾花数据应用该函数时,它将根据鸢尾花标本萼片和花瓣的测量值找到它们的自然分组。使用 K 均值聚类,您必须指定要创建的簇数。
首先,加载数据并调用 kmeans,将所需的簇数设置为 2,并使用平方欧几里德距离。要了解生成的簇区分数据的效果,可以绘制轮廓图。轮廓图显示一个簇中的每个点与相邻簇中的点的接近程度。
load fisheriris [cidx2,cmeans2] = kmeans(meas,2,'dist','sqeuclidean'); [silh2,h] = silhouette(meas,cidx2,'sqeuclidean');
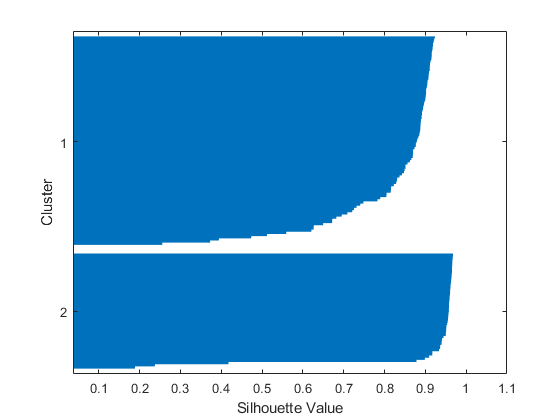
从轮廓图中可以看出,两个簇中的大多数点都具有较大的轮廓值(大于 0.8),表明这些点可以与相邻簇很好地区分。但是,每个簇中还有一些点的轮廓值较低,表示它们靠近其他簇中的点。
事实证明,这些数据中的第四个测量值(花瓣宽度)与第三个测量值(花瓣长度)高度相关,因此前三个测量值的三维图可以很好地表示数据,而无需求助于四个维度。如果绘制数据,则使用不同的符号表示 kmeans 创建的每个簇,就可以识别轮廓值较小的点,也就是与其他簇中的点相距较近的点。
ptsymb = {'bs','r^','md','go','c+'};
for i = 1:2
clust = find(cidx2==i);
plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i});
hold on
end
plot3(cmeans2(:,1),cmeans2(:,2),cmeans2(:,3),'ko');
plot3(cmeans2(:,1),cmeans2(:,2),cmeans2(:,3),'kx');
hold off
xlabel('Sepal Length');
ylabel('Sepal Width');
zlabel('Petal Length');
view(-137,10);
grid on
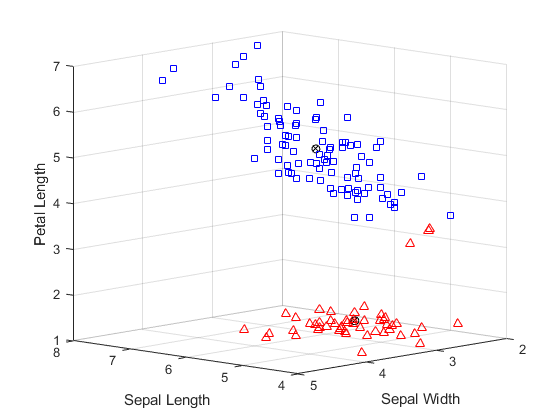
每个簇的质心用带圆圈的 X 表示。下方簇中用三角形表示的点中,有三个非常靠近上方簇中用正方形表示的点。由于上方簇相当分散,这三个点更靠近下方簇的质心而不是上方簇的质心,虽然这些点与所在簇中的大部分点存在明显距离。由于 K 均值聚类只考虑距离而不是密度,因此可能会出现这种结果。
您可以增加簇数以查看 kmeans 是否可以在数据中找到进一步的分组结构。这次,使用可选的 'Display' 名称-值对组参量显示聚类算法中有关每次迭代的信息。
[cidx3,cmeans3] = kmeans(meas,3,'Display','iter');
iter phase num sum
1 1 150 146.424
2 1 5 144.333
3 1 4 143.924
4 1 3 143.61
5 1 1 143.542
6 1 2 143.414
7 1 2 143.023
8 1 2 142.823
9 1 1 142.786
10 1 1 142.754
Best total sum of distances = 142.754
在每次迭代时,kmeans 算法(请参阅 算法)在簇之间重新分配点,以减小点到质心距离的总和,然后重新计算新簇分配的簇质心。请注意,距离总和与重新分配次数随着每次迭代而减小,直到算法达到最小值。kmeans 中使用的算法由两个阶段组成。在此示例中,算法的第二阶段未进行任何重新分配,表明第一阶段在进行几次迭代后就达到了最小值。
默认情况下,kmeans 使用随机选择的一组初始质心位置开始聚类过程。kmeans 算法会收敛于作为局部最小值的解;也就是说,kmeans 可对数据进行分区,使得将任一点移到其他簇都会增加距离总和。但是,同许多其他类型的数值最小化问题一样,kmeans 达到的解有时取决于起点。因此,该数据可能存在其他具有更小距离总和的解(局部最小值)。您可以使用可选的 'Replicates' 名称-值对组参量来检验不同的解。指定多次重复时,kmeans 会在每次重复时从不同的随机选择质心重新开始聚类过程。kmeans 随后返回所有重复中距离总和最小的解。
[cidx3,cmeans3,sumd3] = kmeans(meas,3,'replicates',5,'display','final');
Replicate 1, 9 iterations, total sum of distances = 78.8557. Replicate 2, 10 iterations, total sum of distances = 78.8557. Replicate 3, 8 iterations, total sum of distances = 78.8557. Replicate 4, 8 iterations, total sum of distances = 78.8557. Replicate 5, 1 iterations, total sum of distances = 78.8514. Best total sum of distances = 78.8514
输出表明,即使对于这样相对简单的问题,也存在非全局最小值。这五次重复分别从一组不同的初始质心开始。根据起始位置,kmeans 达到两个不同的解之一。但是,kmeans 最终返回的解是所有重复中距离总和最小的解。第三个输出参量包含每个簇中对于该最佳解的距离总和。
sum(sumd3)
ans = 78.8514
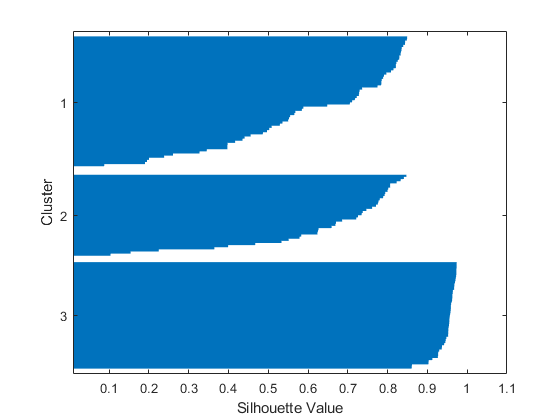
该三簇解的轮廓图显示,有一个簇区分效果很好,但另外两个簇的区别不是很明显。
[silh3,h] = silhouette(meas,cidx3,'sqeuclidean');
同样,您可以绘制原始数据以查看 kmeans 如何将点分配给簇。
for i = 1:3 clust = find(cidx3==i); plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i}); hold on end plot3(cmeans3(:,1),cmeans3(:,2),cmeans3(:,3),'ko'); plot3(cmeans3(:,1),cmeans3(:,2),cmeans3(:,3),'kx'); hold off xlabel('Sepal Length'); ylabel('Sepal Width'); zlabel('Petal Length'); view(-137,10); grid on
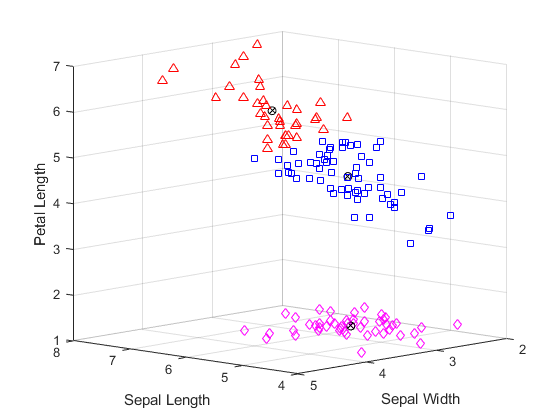
您可以看到,kmeans 已将双簇解中的上方簇一分为二,而且这两个簇非常接近。跟之前的双簇解相比,这个三簇解是否更为有用取决于您在聚类后要对数据进行的操作。silhouette 的第一个输出参量包含每个点的轮廓值,您可以使用这些值对两个解进行定量比较。双簇解的平均轮廓值更大,表明就簇的区分效果而言,这是更好的解。
[mean(silh2) mean(silh3)]
ans =
0.8504 0.7357
您还可以使用不同距离对这些数据进行聚类。余弦距离可能适用于这些数据,因为它会忽略测量值的绝对大小,只考虑相对大小。因此,对于两朵大小不同但花瓣和萼片的形状相似的花,使用平方欧几里德距离可能不接近,但使用余弦距离则会接近。
[cidxCos,cmeansCos] = kmeans(meas,3,'dist','cos');
从轮廓图中可以看出,这些簇的区分效果好像只比使用平方欧几里德距离时稍好一点。
[silhCos,h] = silhouette(meas,cidxCos,'cos');
[mean(silh2) mean(silh3) mean(silhCos)]
ans =
0.8504 0.7357 0.7491

请注意,簇的顺序与之前的轮廓图不一样。这是因为 kmeans 会随机选择初始簇分配。
通过绘制原始数据,您可以看到使用两种不同距离创建的簇在形状上的差异。两个解较为相似,但使用余弦距离时,上方的两个簇向原点拉伸。
for i = 1:3 clust = find(cidxCos==i); plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i}); hold on end hold off xlabel('Sepal Length'); ylabel('Sepal Width'); zlabel('Petal Length'); view(-137,10); grid on
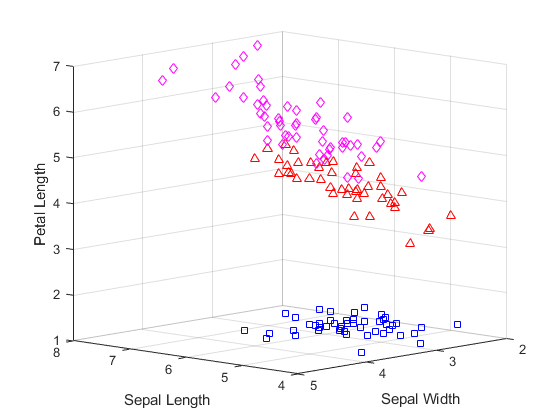
此图不包括簇质心,因为使用余弦距离时,质心是以原始数据空间原点为起点的射线。但是,您可以绘制归一化数据点的平行坐标图,以直观地了解簇质心的差异。
lnsymb = {'b-','r-','m-'};
names = {'SL','SW','PL','PW'};
meas0 = meas ./ repmat(sqrt(sum(meas.^2,2)),1,4);
ymin = min(min(meas0));
ymax = max(max(meas0));
for i = 1:3
subplot(1,3,i);
plot(meas0(cidxCos==i,:)',lnsymb{i});
hold on;
plot(cmeansCos(i,:)','k-','LineWidth',2);
hold off;
title(sprintf('Cluster %d',i));
xlim([.9, 4.1]);
ylim([ymin, ymax]);
h_gca = gca;
h_gca.XTick = 1:4;
h_gca.XTickLabel = names;
end

从图中可以清楚地看出,三个簇所包含的标本在花瓣和萼片的平均相对大小方面明显不同。第一个簇的花瓣严格小于萼片。后面两个簇的花瓣和萼片的大小重叠,但第三个簇的重叠超过第二个簇。您还可以看到,第二个和第三个簇包含一些非常相似的标本。
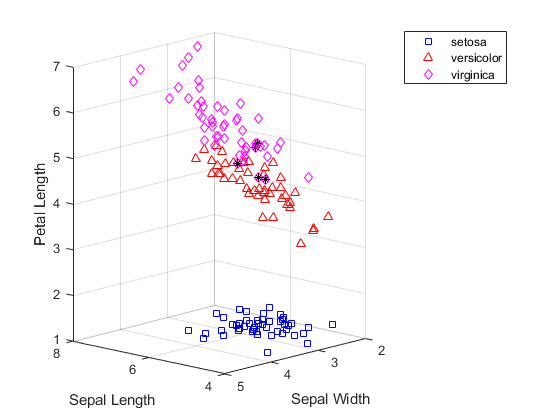
因为我们知道数据中每个观测值所属的品种,所以可以将 kmeans 发现的簇与实际品种进行比较,以了解这三个品种是否具有明显不同的物理特性。实际上,如下图所示,使用余弦距离创建的簇与实际品种分组的不同之处只有五朵花。这五个点(用星形标记绘制)都靠近上方两个簇的边缘交界处。
subplot(1,1,1); for i = 1:3 clust = find(cidxCos==i); plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i}); hold on end xlabel('Sepal Length'); ylabel('Sepal Width'); zlabel('Petal Length'); view(-137,10); grid on sidx = grp2idx(species); miss = find(cidxCos ~= sidx); plot3(meas(miss,1),meas(miss,2),meas(miss,3),'k*'); legend({'setosa','versicolor','virginica'}); hold off
使用层次聚类方法对 Fisher 鸢尾花数据进行聚类
K 均值聚类只产生一个鸢尾花数据分区,但您可能还想按照不同的分组尺度来研究数据。要实现这一点,您可以通过层次聚类创建层次聚类树。
首先,使用鸢尾花数据中观测值之间的距离创建一个聚类树。先使用欧几里德距离。
eucD = pdist(meas,'euclidean'); clustTreeEuc = linkage(eucD,'average');
共性相关是验证聚类树与原始距离是否一致的一种方法。较大的值表明树对距离的拟合良好,即观测值之间的两两连接与它们实际上的两两距离是相关的。此树对距离的拟合看起来相当好。
cophenet(clustTreeEuc,eucD)
ans =
0.8770
要可视化聚类的层次结构,可以绘制树状图。
[h,nodes] = dendrogram(clustTreeEuc,0);
h_gca = gca;
h_gca.TickDir = 'out';
h_gca.TickLength = [.002 0];
h_gca.XTickLabel = [];

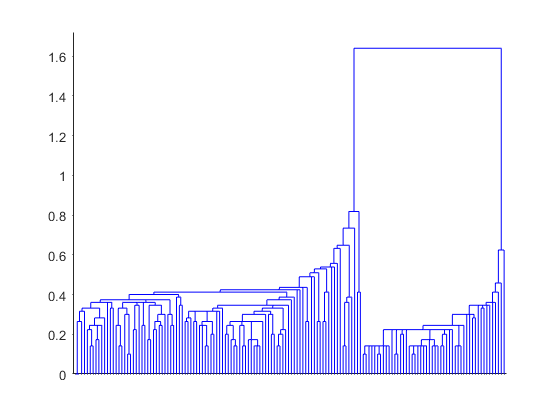
树中的根节点远远高于其余节点,证实了您在 K 均值聚类中所看到的:两个很大的、区别明显的观测值组。在每个组中可以看到,随着距离尺度越来越小,较低级别的组逐渐出现。有许多级别不同、大小不同、区别度不同的组。
根据 K 均值聚类的结果,我们也不妨使用余弦来测度距离。由此生成的层次结构树很不一样,让我们能够以一种完全不同的方式观察鸢尾花数据的组结构。
cosD = pdist(meas,'cosine'); clustTreeCos = linkage(cosD,'average'); cophenet(clustTreeCos,cosD)
ans =
0.9360
[h,nodes] = dendrogram(clustTreeCos,0);
h_gca = gca;
h_gca.TickDir = 'out';
h_gca.TickLength = [.002 0];
h_gca.XTickLabel = [];

此树的最高级别将鸢尾花标本分成两个区别很大的组。树状图显示,使用余弦距离,相对于组间差异的组内差异远小于使用欧几里德距离的情况。这正是您期望的数据结果,因为对于从原点出发的相同“方向”上的对象,余弦距离将其两两距离计为零。
包含 150 个观测值的图较为杂乱,但您可以制作简化的树状图,不显示树中靠近底部的级别。
[h,nodes] = dendrogram(clustTreeCos,12);
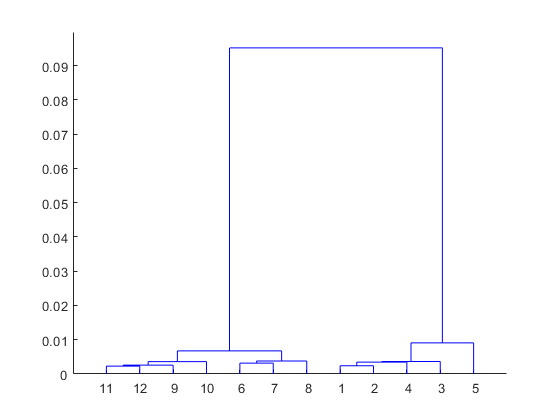
此树中的三个最高节点划分出三个大小相同的组,以及一个与任何其他组都不相近的标本(标记为叶节点 5)。
[sum(ismember(nodes,[11 12 9 10])) sum(ismember(nodes,[6 7 8])) ...
sum(ismember(nodes,[1 2 4 3])) sum(nodes==5)]
ans =
54 46 49 1
在很多情况下,树状图结果或许已能满足分类要求。但是,您可以更进一步,使用 cluster 函数来裁剪树并将观测值显式划分为特定的聚类,就像使用 K 均值一样。根据使用余弦距离的层次结构创建聚类,指定连接高度以在三个最高节点下方裁剪树,创建四个聚类,然后绘制经过聚类的原始数据。
hidx = cluster(clustTreeCos,'criterion','distance','cutoff',.006); for i = 1:5 clust = find(hidx==i); plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i}); hold on end hold off xlabel('Sepal Length'); ylabel('Sepal Width'); zlabel('Petal Length'); view(-137,10); grid on

此图显示,就其性质而言,使用余弦距离的层次聚类结果与三簇 K 均值聚类的结果类似。但是,创建层次聚类树可以一次性可视化所有结果,而在 K 均值聚类中需要使用不同的 K 值进行大量试验。
层次聚类还允许您使用不同的连接进行试验。例如,相比基于平均距离连接聚类,基于单连接对鸢尾花数据进行聚类时,往往将距离更大的对象连接在一起,从而给出对数据结构的另一种解释。
clustTreeSng = linkage(eucD,'single'); [h,nodes] = dendrogram(clustTreeSng,0); h_gca = gca; h_gca.TickDir = 'out'; h_gca.TickLength = [.002 0]; h_gca.XTickLabel = [];