kmeans

k-means clustering

Syntax

idx = kmeans(X,k)

idx = kmeans(X,k,Name,Value)

[idx,C]
= kmeans(___)

[idx,C,sumd]
= kmeans(___)

[idx,C,sumd,D]
= kmeans(___)

Description

idx = kmeans(X,k) performs k-means clustering to partition the observations of the n-by-p data matrix X into k clusters, and returns an n-by-1 vector (idx) containing cluster indices of each observation. Rows of X correspond to points and columns correspond to variables.

By default, kmeans uses the squared Euclidean distance metric and the k-means++ algorithm for cluster center initialization.

example

idx = kmeans(X,k,Name,Value) returns the cluster indices with additional options specified by one or more Name,Value pair arguments.

For example, specify the cosine distance, the number of times to repeat the clustering using new initial values, or to use parallel computing.

example

[idx,C] = kmeans(___) returns the k cluster centroid locations in the k-by-p matrix C.

example

[idx,C,sumd] = kmeans(___) returns the within-cluster sums of point-to-centroid distances in the k-by-1 vector sumd.

example

[idx,C,sumd,D] = kmeans(___) returns distances from each point to every centroid in the n-by-k matrix D.

example

Examples

collapse all

Train a k-Means Clustering Algorithm

Open Live Script

Cluster data using k-means clustering, then plot the cluster regions.

Load Fisher's iris data set. Use the petal lengths and widths as predictors.

load fisheriris
X = meas(:,3:4);

figure;
plot(X(:,1),X(:,2),'k*','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)'; 
ylabel 'Petal Widths (cm)';

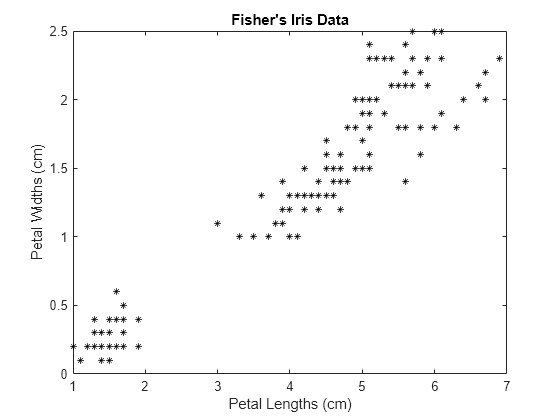
Figure contains an axes object. The axes object with title Fisher's Iris Data, xlabel Petal Lengths (cm), ylabel Petal Widths (cm) contains a line object which displays its values using only markers.

The larger cluster seems to be split into a lower variance region and a higher variance region. This might indicate that the larger cluster is two, overlapping clusters.

Cluster the data. Specify k = 3 clusters.

rng(1); % For reproducibility
[idx,C] = kmeans(X,3);

idx is a vector of predicted cluster indices corresponding to the observations in X. C is a 3-by-2 matrix containing the final centroid locations.

Use kmeans to compute the distance from each centroid to points on a grid. To do this, pass the centroids (C) and points on a grid to kmeans, and implement one iteration of the algorithm.

x1 = min(X(:,1)):0.01:max(X(:,1));
x2 = min(X(:,2)):0.01:max(X(:,2));
[x1G,x2G] = meshgrid(x1,x2);
XGrid = [x1G(:),x2G(:)]; % Defines a fine grid on the plot

idx2Region = kmeans(XGrid,3,'MaxIter',1,'Start',C);

Warning: Failed to converge in 1 iterations.

    % Assigns each node in the grid to the closest centroid

kmeans displays a warning stating that the algorithm did not converge, which you should expect since the software only implemented one iteration.

Plot the cluster regions.

figure;
gscatter(XGrid(:,1),XGrid(:,2),idx2Region,...
    [0,0.75,0.75;0.75,0,0.75;0.75,0.75,0],'..');
hold on;
plot(X(:,1),X(:,2),'k*','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)';
ylabel 'Petal Widths (cm)'; 
legend('Region 1','Region 2','Region 3','Data','Location','SouthEast');
hold off;

Figure contains an axes object. The axes object with title Fisher's Iris Data, xlabel Petal Lengths (cm), ylabel Petal Widths (cm) contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent Region 1, Region 2, Region 3, Data.

Partition Data into Two Clusters

Open Live Script

Randomly generate the sample data.

rng default; % For reproducibility
X = [randn(100,2)*0.75+ones(100,2);
    randn(100,2)*0.5-ones(100,2)];

figure;
plot(X(:,1),X(:,2),'.');
title 'Randomly Generated Data';

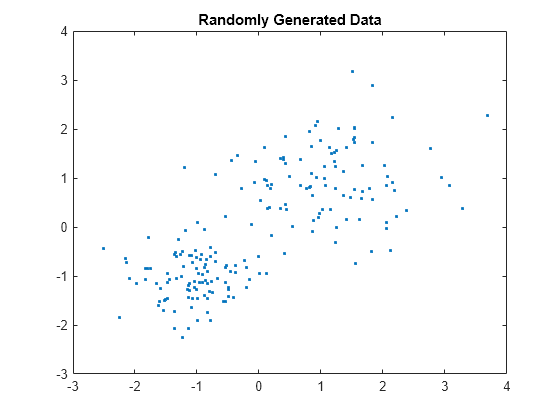
Figure contains an axes object. The axes object with title Randomly Generated Data contains a line object which displays its values using only markers.

There appears to be two clusters in the data.

Partition the data into two clusters, and choose the best arrangement out of five initializations. Display the final output.

opts = statset('Display','final');
[idx,C] = kmeans(X,2,'Distance','cityblock',...
    'Replicates',5,'Options',opts);

Replicate 1, 3 iterations, total sum of distances = 201.533.
Replicate 2, 5 iterations, total sum of distances = 201.533.
Replicate 3, 3 iterations, total sum of distances = 201.533.
Replicate 4, 3 iterations, total sum of distances = 201.533.
Replicate 5, 2 iterations, total sum of distances = 201.533.
Best total sum of distances = 201.533

By default, the software initializes the replicates separately using k-means++.

Plot the clusters and the cluster centroids.

figure;
plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12)
hold on
plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12)
plot(C(:,1),C(:,2),'kx',...
     'MarkerSize',15,'LineWidth',3) 
legend('Cluster 1','Cluster 2','Centroids',...
       'Location','NW')
title 'Cluster Assignments and Centroids'
hold off

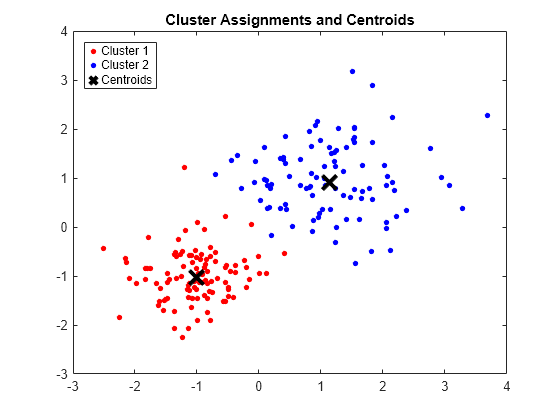
Figure contains an axes object. The axes object with title Cluster Assignments and Centroids contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Cluster 1, Cluster 2, Centroids.

You can determine how well separated the clusters are by passing idx to silhouette.

Cluster Data Using Parallel Computing

This example uses:

Open Live Script

Clustering large data sets might take time, particularly if you use online updates (set by default). If you have a Parallel Computing Toolbox ™ license and you set the options for parallel computing, then kmeans runs each clustering task (or replicate) in parallel. And, if Replicates>1, then parallel computing decreases time to convergence.

Randomly generate a large data set from a Gaussian mixture model.

rng(1); % For reproducibility
Mu = ones(20,30).*(1:20)'; % Gaussian mixture mean
rn30 = randn(30,30);
Sigma = rn30'*rn30; % Symmetric and positive-definite covariance
Mdl = gmdistribution(Mu,Sigma); % Define the Gaussian mixture distribution

X = random(Mdl,10000);

Mdl is a 30-dimensional gmdistribution model with 20 components. X is a 10000-by-30 matrix of data generated from Mdl.

Specify the options for parallel computing.

stream = RandStream('mlfg6331_64');  % Random number stream
options = statset('UseParallel',1,'UseSubstreams',1,...
    'Streams',stream);

The input argument 'mlfg6331_64' of RandStream specifies to use the multiplicative lagged Fibonacci generator algorithm. options is a structure array with fields that specify options for controlling estimation.

Cluster the data using k-means clustering. Specify that there are k = 20 clusters in the data and increase the number of iterations. Typically, the objective function contains local minima. Specify 10 replicates to help find a lower, local minimum.

tic; % Start stopwatch timer
[idx,C,sumd,D] = kmeans(X,20,'Options',options,'MaxIter',10000,...
    'Display','final','Replicates',10);

Starting parallel pool (parpool) using the 'Processes' profile ...
Connected to the parallel pool (number of workers: 6).
Replicate 4, 79 iterations, total sum of distances = 7.62412e+06.
Replicate 2, 56 iterations, total sum of distances = 7.62036e+06.
Replicate 3, 76 iterations, total sum of distances = 7.62583e+06.
Replicate 6, 96 iterations, total sum of distances = 7.6258e+06.
Replicate 5, 103 iterations, total sum of distances = 7.61753e+06.
Replicate 1, 94 iterations, total sum of distances = 7.60746e+06.
Replicate 10, 66 iterations, total sum of distances = 7.62582e+06.
Replicate 8, 113 iterations, total sum of distances = 7.60741e+06.
Replicate 9, 80 iterations, total sum of distances = 7.60592e+06.
Replicate 7, 77 iterations, total sum of distances = 7.61939e+06.
Best total sum of distances = 7.60592e+06

toc % Terminate stopwatch timer

Elapsed time is 72.873647 seconds.

The Command Window indicates that six workers are available. The number of workers might vary on your system. The Command Window displays the number of iterations and the terminal objective function value for each replicate. The output arguments contain the results of replicate 9 because it has the lowest total sum of distances.

Assign New Data to Existing Clusters and Generate C/C++ Code

This example uses:

Open Live Script

kmeans performs k-means clustering to partition data into k clusters. When you have a new data set to cluster, you can create new clusters that include the existing data and the new data by using kmeans. The kmeans function supports C/C++ code generation, so you can generate code that accepts training data and returns clustering results, and then deploy the code to a device. In this workflow, you must pass training data, which can be of considerable size. To save memory on the device, you can separate training and prediction by using kmeans and pdist2, respectively.

Use kmeans to create clusters in MATLAB® and use pdist2 in the generated code to assign new data to existing clusters. For code generation, define an entry-point function that accepts the cluster centroid positions and the new data set, and returns the index of the nearest cluster. Then, generate code for the entry-point function.

Generating C/C++ code requires MATLAB® Coder™.

Perform k-Means Clustering

Generate a training data set using three distributions.

rng('default') % For reproducibility
X = [randn(100,2)*0.75+ones(100,2);
    randn(100,2)*0.5-ones(100,2);
    randn(100,2)*0.75];

Partition the training data into three clusters by using kmeans.

[idx,C] = kmeans(X,3);

Plot the clusters and the cluster centroids.

figure
gscatter(X(:,1),X(:,2),idx,'bgm')
hold on
plot(C(:,1),C(:,2),'kx')
legend('Cluster 1','Cluster 2','Cluster 3','Cluster Centroid')

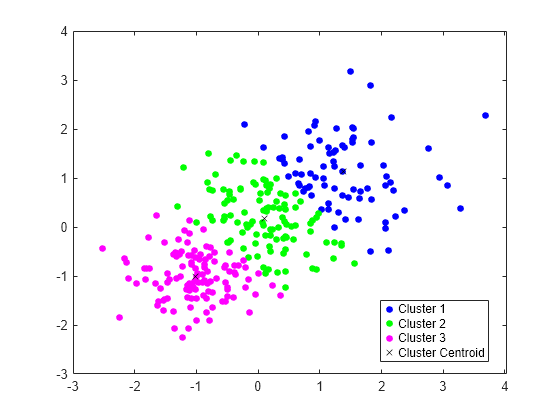
Figure contains an axes object. The axes object contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent Cluster 1, Cluster 2, Cluster 3, Cluster Centroid.

Assign New Data to Existing Clusters

Generate a test data set.

Xtest = [randn(10,2)*0.75+ones(10,2);
    randn(10,2)*0.5-ones(10,2);
    randn(10,2)*0.75];

Classify the test data set using the existing clusters. Find the nearest centroid from each test data point by using pdist2.

[~,idx_test] = pdist2(C,Xtest,'euclidean','Smallest',1);

Plot the test data and label the test data using idx_test by using gscatter.

gscatter(Xtest(:,1),Xtest(:,2),idx_test,'bgm','ooo')
legend('Cluster 1','Cluster 2','Cluster 3','Cluster Centroid', ...
    'Data classified to Cluster 1','Data classified to Cluster 2', ...
    'Data classified to Cluster 3')

Figure contains an axes object. The axes object contains 7 objects of type line. One or more of the lines displays its values using only markers These objects represent Cluster 1, Cluster 2, Cluster 3, Cluster Centroid, Data classified to Cluster 1, Data classified to Cluster 2, Data classified to Cluster 3.

Generate Code

Generate C code that assigns new data to the existing clusters. Note that generating C/C++ code requires MATLAB® Coder™.

Define an entry-point function named findNearestCentroid that accepts centroid positions and new data, and then find the nearest cluster by using pdist2.

Add the %#codegen compiler directive (or pragma) to the entry-point function after the function signature to indicate that you intend to generate code for the MATLAB algorithm. Adding this directive instructs the MATLAB Code Analyzer to help you diagnose and fix violations that would cause errors during code generation.

type findNearestCentroid % Display contents of findNearestCentroid.m

function idx = findNearestCentroid(C,X) %#codegen
[~,idx] = pdist2(C,X,'euclidean','Smallest',1); % Find the nearest centroid

Note: If you click the button located in the upper-right section of this page and open this example in MATLAB®, then MATLAB® opens the example folder. This folder includes the entry-point function file.

Generate code by using codegen (MATLAB Coder). Because C and C++ are statically typed languages, you must determine the properties of all variables in the entry-point function at compile time. To specify the data type and array size of the inputs of findNearestCentroid, pass a MATLAB expression that represents the set of values with a certain data type and array size by using the -args option. For details, see Specify Variable-Size Arguments for Code Generation.

codegen findNearestCentroid -args {C,Xtest}

Code generation successful.

codegen generates the MEX function findNearestCentroid_mex with a platform-dependent extension.

Verify the generated code.

myIndx = findNearestCentroid(C,Xtest);
myIndex_mex = findNearestCentroid_mex(C,Xtest);
verifyMEX = isequal(idx_test,myIndx,myIndex_mex)

verifyMEX = logical
   1

isequal returns logical 1 (true), which means all the inputs are equal. The comparison confirms that the pdist2 function, the findNearestCentroid function, and the MEX function return the same index.

You can also generate optimized CUDA® code using GPU Coder™.

cfg = coder.gpuConfig('mex');
codegen -config cfg findNearestCentroid -args {C,Xtest}

For more information on code generation, see General Code Generation Workflow. For more information on GPU coder, see Get Started with GPU Coder (GPU Coder) and Supported Functions (GPU Coder).

Input Arguments

collapse all

`X` — Data
numeric matrix

Data, specified as a numeric matrix. The rows of X correspond to observations, and the columns correspond to variables.

If X is a numeric vector, then kmeans treats it as an n-by-1 data matrix, regardless of its orientation.

The software treats NaNs in X as missing data and removes any row of X that contains at least one NaN. Removing rows of X reduces the sample size. The kmeans function returns NaN for the corresponding value in the output argument idx.

Data Types: single | double

`k` — Number of clusters
positive integer

Number of clusters in the data, specified as a positive integer.

Data Types: single | double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Distance','cosine','Replicates',10,'Options',statset('UseParallel',1) specifies the cosine distance, 10 replicate clusters at different starting values, and to use parallel computing.

`Display` — Level of output to display
`'off'` (default) | `'final'` | `'iter'`

Level of output to display in the Command Window, specified as the comma-separated pair consisting of 'Display' and one of the following options:

'final' — Displays results of the final iteration
'iter' — Displays results of each iteration
'off' — Displays nothing

When you specify 'iter', the software displays the following information after each iteration:

Iteration number
Phase, where 1 corresponds to the batch update phase, and 2 corresponds to the online update phase (see Algorithms)
Number of points reassigned to a different cluster during the iteration
Sum of the point-to-cluster-centroid distances

Example: 'Display','final'

`Distance` — Distance metric
`'sqeuclidean'` (default) | `'cityblock'` | `'cosine'` | `'correlation'` | `'hamming'`

Distance metric, in p-dimensional space, used for minimization, specified as the comma-separated pair consisting of 'Distance' and 'sqeuclidean', 'cityblock', 'cosine', 'correlation', or 'hamming'.

kmeans computes centroid clusters differently for the supported distance metrics. This table summarizes the available distance metrics. In the formulae, x is an observation (that is, a row of X) and c is a centroid (a row vector).

Distance Metric	Description	Formula
`'sqeuclidean'`	Squared Euclidean distance (default). Each centroid is the mean of the points in that cluster.	$d (x, c) = (x - c) (x - c)^{'}$
`'cityblock'`	Sum of absolute differences, i.e., the L1 distance. Each centroid is the component-wise median of the points in that cluster.	$d (x, c) = \sum_{j = 1}^{p} \| x_{j} - c_{j} \|$
`'cosine'`	One minus the cosine of the included angle between points (treated as vectors). Each centroid is the mean of the points in that cluster, after normalizing those points to unit Euclidean length.	$d (x, c) = 1 - \frac{x c'}{\sqrt{(x x^{'}) (c c')}}$
`'correlation'`	One minus the sample correlation between points (treated as sequences of values). Each centroid is the component-wise mean of the points in that cluster, after centering and normalizing those points to zero mean and unit standard deviation.	$d (x, c) = 1 - \frac{(x - \vec{\bar{x}}) {(c - \vec{\bar{c}})}^{'}}{\sqrt{(x - \vec{\bar{x}}) {(x - \vec{\bar{x}})}^{'}} \sqrt{(c - \vec{\bar{c}}) {(c - \vec{\bar{c}})}^{'}}},$ where $\vec{\bar{x}} = \frac{1}{p} (\sum_{j = 1}^{p} x_{j}) {\vec{1}}_{p}$ $\vec{\bar{c}} = \frac{1}{p} (\sum_{j = 1}^{p} c_{j}) {\vec{1}}_{p}$ ${\vec{1}}_{p}$ is a row vector of p ones.
`'hamming'`	This metric is only suitable for binary data. It is the proportion of bits that differ. Each centroid is the component-wise median of points in that cluster.	$d (x, y) = \frac{1}{p} \sum_{j = 1}^{p} I {x_{j} \neq y_{j}},$ where I is the indicator function.

Example: 'Distance','cityblock'

`EmptyAction` — Action to take if cluster loses all member observations
`'singleton'` (default) | `'error'` | `'drop'`

Action to take if a cluster loses all its member observations, specified as the comma-separated pair consisting of 'EmptyAction' and one of the following options.

Value	Description
`'error'`	Treat an empty cluster as an error.
`'drop'`	Remove any clusters that become empty. `kmeans` sets the corresponding return values in `C` and `D` to `NaN`.
`'singleton'`	Create a new cluster consisting of the one point furthest from its centroid (default).

Example: 'EmptyAction','error'

`MaxIter` — Maximum number of iterations
`100` (default) | positive integer

Maximum number of iterations, specified as the comma-separated pair consisting of 'MaxIter' and a positive integer.

Example: 'MaxIter',1000

Data Types: double | single

`OnlinePhase` — Online update flag
`'off'` (default) | `'on'`

Online update flag, specified as the comma-separated pair consisting of 'OnlinePhase' and 'off' or 'on'.

If OnlinePhase is on, then kmeans performs an online update phase in addition to a batch update phase. The online phase can be time consuming for large data sets, but guarantees a solution that is a local minimum of the distance criterion. In other words, the software finds a partition of the data in which moving any single point to a different cluster increases the total sum of distances.

Example: 'OnlinePhase','on'

`Options` — Options for controlling iterative algorithm for minimizing fitting criteria
`[]` (default) | structure array returned by `statset`

Options for controlling the iterative algorithm for minimizing the fitting criteria, specified as the comma-separated pair consisting of 'Options' and a structure array returned by statset. Supported fields of the structure array specify options for controlling the iterative algorithm.

This table summarizes the supported fields. Note that the supported fields require Parallel Computing Toolbox™.

Field Description

Field	Description
`'Streams'`	A `RandStream` object or cell array of such objects. If you do not specify `Streams`, `kmeans` uses the default stream or streams. If you specify `Streams`, use a single object except when all of the following conditions exist: You have an open parallel pool. `UseParallel` is `true`. `UseSubstreams` is `false`. In this case, use a cell array the same size as the parallel pool. If a parallel pool is not open, then `Streams` must supply a single random number stream.
`'UseParallel'`	If `true` and `Replicates` > 1, then `kmeans` implements the k-means algorithm on each replicate in parallel. If Parallel Computing Toolbox is not installed, then computation occurs in serial mode. The default is `false`, indicating serial computation.
`'UseSubstreams'`	Set to `true` to compute in a reproducible fashion. The default is `false`. To compute reproducibly, set `Streams` to a type allowing substreams: `'mlfg6331_64'` or `'mrg32k3a'`.

'Streams'

A RandStream object or cell array of such objects. If you do not specify Streams, kmeans uses the default stream or streams. If you specify Streams, use a single object except when all of the following conditions exist:

You have an open parallel pool.
UseParallel is true.
UseSubstreams is false.

In this case, use a cell array the same size as the parallel pool. If a parallel pool is not open, then Streams must supply a single random number stream.

'UseParallel'

If true and Replicates > 1, then kmeans implements the k-means algorithm on each replicate in parallel.
If Parallel Computing Toolbox is not installed, then computation occurs in serial mode. The default is false, indicating serial computation.

'UseSubstreams' Set to true to compute in a reproducible fashion. The default is false. To compute reproducibly, set Streams to a type allowing substreams: 'mlfg6331_64' or 'mrg32k3a'.

To ensure more predictable results, use parpool (Parallel Computing Toolbox) and explicitly create a parallel pool before invoking kmeans and setting 'Options',statset('UseParallel',1).

Example: 'Options',statset('UseParallel',1)

Data Types: struct

`Replicates` — Number of times to repeat clustering using new initial cluster centroid positions
`1` (default) | positive integer

Number of times to repeat clustering using new initial cluster centroid positions, specified as the comma-separated pair consisting of 'Replicates' and an integer. kmeans returns the solution with the lowest sumd.

You can set 'Replicates' implicitly by supplying a 3-D array as the value for the 'Start' name-value pair argument.

Example: 'Replicates',5

Data Types: double | single

`Start` — Method for choosing initial cluster centroid positions
`'plus'` (default) | `'cluster'` | `'sample'` | `'uniform'` | numeric matrix | numeric array

Method for choosing initial cluster centroid positions (or seeds), specified as the comma-separated pair consisting of 'Start' and 'cluster', 'plus', 'sample', 'uniform', a numeric matrix, or a numeric array. This table summarizes the available options for choosing seeds.

Value	Description
`'cluster'`	Perform a preliminary clustering phase on a random 10% subsample of `X` when the number of observations in the subsample is greater than `k`. This preliminary phase is itself initialized using `'sample'`. If the number of observations in the random 10% subsample is less than `k`, then the software selects `k` observations from `X` at random.
`'plus'` (default)	Select `k` seeds by implementing the k-means++ algorithm for cluster center initialization.
`'sample'`	Select `k` observations from `X` at random.
`'uniform'`	Select `k` points uniformly at random from the range of `X`. Not valid with the Hamming distance.
numeric matrix	`k`-by-p matrix of centroid starting locations. The rows of `Start` correspond to seeds. The software infers `k` from the first dimension of `Start`, so you can pass in `[]` for `k`.
numeric array	`k`-by-p-by-r array of centroid starting locations. The rows of each page correspond to seeds. The third dimension invokes replication of the clustering routine. Page j contains the set of seeds for replicate j. The software infers the number of replicates (specified by the `'Replicates'` name-value pair argument) from the size of the third dimension.

Example: 'Start','sample'

Data Types: char | string | double | single

Output Arguments

collapse all

`idx` — Cluster indices
numeric column vector

Cluster indices, returned as a numeric column vector. idx has as many rows as X, and each row indicates the cluster assignment of the corresponding observation.

`C` — Cluster centroid locations
numeric matrix

Cluster centroid locations, returned as a numeric matrix. C is a k-by-p matrix, where row j is the centroid of cluster j. The location of a centroid depends on the distance metric specified by the Distance name-value argument.

`sumd` — Within-cluster sums of point-to-centroid distances
numeric column vector

Within-cluster sums of point-to-centroid distances, returned as a numeric column vector. sumd is a k-by-1 vector, where element j is the sum of point-to-centroid distances within cluster j. By default, kmeans uses the squared Euclidean distance (see 'Distance' metrics).

`D` — Distances from each point to every centroid
numeric matrix

Distances from each point to every centroid, returned as a numeric matrix. D is an n-by-k matrix, where element (j,m) is the distance from observation j to centroid m. By default, kmeans uses the squared Euclidean distance (see 'Distance' metrics).

More About

collapse all

k-Means Clustering

k-means clustering, or Lloyd’s algorithm [2], is an iterative, data-partitioning algorithm that assigns n observations to exactly one of k clusters defined by centroids, where k is chosen before the algorithm starts.

The algorithm proceeds as follows:

Choose k initial cluster centers (centroid). For example, choose k observations at random (by using 'Start','sample') or use the k-means ++ algorithm for cluster center initialization (the default).
Compute point-to-cluster-centroid distances of all observations to each centroid.
There are two ways to proceed (specified by OnlinePhase):
- Batch update — Assign each observation to the cluster with the closest centroid.
- Online update — Individually assign observations to a different centroid if the reassignment decreases the sum of the within-cluster, sum-of-squares point-to-cluster-centroid distances.
For more details, see Algorithms.
Compute the average of the observations in each cluster to obtain k new centroid locations.
Repeat steps 2 through 4 until cluster assignments do not change, or the maximum number of iterations is reached.

k-means++ Algorithm

The k-means++ algorithm uses an heuristic to find centroid seeds for k-means clustering. According to Arthur and Vassilvitskii [1], k-means++ improves the running time of Lloyd’s algorithm, and the quality of the final solution.

The k-means++ algorithm chooses seeds as follows, assuming the number of clusters is k.

Select an observation uniformly at random from the data set, X. The chosen observation is the first centroid, and is denoted c₁.
Compute distances from each observation to c₁. Denote the distance between c_j and the observation m as $d (x_{m}, c_{j})$ .
Select the next centroid, c₂ at random from X with probability

$\frac{d^{2} (x_{m}, c_{1})}{\sum_{j = 1}^{n} d^{2} (x_{j}, c_{1})} .$
To choose center j:
1. Compute the distances from each observation to each centroid, and assign each observation to its closest centroid.
2. For m = 1,...,n and p = 1,...,j – 1, select centroid j at random from X with probability
  
  $\frac{d^{2} (x_{m}, c_{p})}{\sum_{{h; x_{h} \in C_{p}}}^{} d^{2} (x_{h}, c_{p})},$
  where C_p is the set of all observations closest to centroid c_p and x_m belongs to C_p.
  That is, select each subsequent center with a probability proportional to the distance from itself to the closest center that you already chose.
Repeat step 4 until k centroids are chosen.

Arthur and Vassilvitskii [1] demonstrate, using a simulation study for several cluster orientations, that k-means++ achieves faster convergence to a lower sum of within-cluster, sum-of-squares point-to-cluster-centroid distances than Lloyd’s algorithm.

Algorithms

kmeans uses a two-phase iterative algorithm to minimize the sum of point-to-centroid distances, summed over all k clusters.
1. This first phase uses batch updates, where each iteration consists of reassigning points to their nearest cluster centroid, all at once, followed by recalculation of cluster centroids. This phase occasionally does not converge to solution that is a local minimum. That is, a partition of the data where moving any single point to a different cluster increases the total sum of distances. This is more likely for small data sets. The batch phase is fast, but potentially only approximates a solution as a starting point for the second phase.
2. This second phase uses online updates, where points are individually reassigned if doing so reduces the sum of distances, and cluster centroids are recomputed after each reassignment. Each iteration during this phase consists of one pass though all the points. This phase converges to a local minimum, although there might be other local minima with lower total sum of distances. In general, finding the global minimum is solved by an exhaustive choice of starting points, but using several replicates with random starting points typically results in a solution that is a global minimum.
If Replicates = r > 1 and Start is plus (the default), then the software selects r possibly different sets of seeds according to the k-means++ algorithm.
If you enable the UseParallel option in Options and Replicates > 1, then each worker selects seeds and clusters in parallel.

References

[1] Arthur, David, and Sergi Vassilvitskii. “K-means++: The Advantages of Careful Seeding.” SODA ‘07: Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms. 2007, pp. 1027–1035.

[2] Lloyd, Stuart P. “Least Squares Quantization in PCM.” IEEE Transactions on Information Theory. Vol. 28, 1982, pp. 129–137.

[3] Seber, G. A. F. Multivariate Observations. Hoboken, NJ: John Wiley & Sons, Inc., 1984.

[4] Spath, H. Cluster Dissection and Analysis: Theory, FORTRAN Programs, Examples. Translated by J. Goldschmidt. New York: Halsted Press, 1985.

Extended Capabilities

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

Usage notes and limitations:

Supported syntaxes are:
- idx = kmeans(X,k)
- [idx,C] = kmeans(X,k)
- [idx,C,sumd] = kmeans(X,k)
- [___] = kmeans(___,Name,Value)
Supported name-value pair arguments, and any differences, are:
- 'Display' — Default value is 'iter'.
- 'MaxIter'
- 'Options' — Supports only the 'TolFun' field of the structure array created by statset. The default value of 'TolFun' is 1e-4. The kmeans function uses the value of 'TolFun' as the termination tolerance for the within-cluster sums of point-to-centroid distances. For example, you can specify 'Options',statset('TolFun',1e-8).
- 'Replicates'
- 'Start' — Supports only 'plus', 'sample', and a numeric array.

For more information, see Tall Arrays for Out-of-Memory Data.

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

For more information on code generation, see Introduction to Code Generation and General Code Generation Workflow.

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

To run in parallel, specify the Options name-value argument in the call to this function and set the UseParallel field of the options structure to true using statset:

Options=statset(UseParallel=true)

For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced before R2006a

kmeans

Syntax

Description

Examples

Train a k-Means Clustering Algorithm

Partition Data into Two Clusters

Cluster Data Using Parallel Computing

Assign New Data to Existing Clusters and Generate C/C++ Code

Input Arguments

`X` — Data
numeric matrix

`k` — Number of clusters
positive integer

Name-Value Arguments

`Display` — Level of output to display
`'off'` (default) | `'final'` | `'iter'`

`Distance` — Distance metric
`'sqeuclidean'` (default) | `'cityblock'` | `'cosine'` | `'correlation'` | `'hamming'`

`EmptyAction` — Action to take if cluster loses all member observations
`'singleton'` (default) | `'error'` | `'drop'`

`MaxIter` — Maximum number of iterations
`100` (default) | positive integer

`OnlinePhase` — Online update flag
`'off'` (default) | `'on'`

`Options` — Options for controlling iterative algorithm for minimizing fitting criteria
`[]` (default) | structure array returned by `statset`

`Replicates` — Number of times to repeat clustering using new initial cluster centroid positions
`1` (default) | positive integer

`Start` — Method for choosing initial cluster centroid positions
`'plus'` (default) | `'cluster'` | `'sample'` | `'uniform'` | numeric matrix | numeric array

Output Arguments

`idx` — Cluster indices
numeric column vector

`C` — Cluster centroid locations
numeric matrix

`sumd` — Within-cluster sums of point-to-centroid distances
numeric column vector

`D` — Distances from each point to every centroid
numeric matrix

More About

k-Means Clustering

k-means++ Algorithm

Algorithms

References

Extended Capabilities

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Version History

See Also

Topics

External Websites

kmeans

Syntax

Description

Examples

Train a k-Means Clustering Algorithm

Partition Data into Two Clusters

Cluster Data Using Parallel Computing

Assign New Data to Existing Clusters and Generate C/C++ Code

Input Arguments

X — Data numeric matrix

k — Number of clusters positive integer

Name-Value Arguments

Display — Level of output to display 'off' (default) | 'final' | 'iter'

Distance — Distance metric 'sqeuclidean' (default) | 'cityblock' | 'cosine' | 'correlation' | 'hamming'

EmptyAction — Action to take if cluster loses all member observations 'singleton' (default) | 'error' | 'drop'

MaxIter — Maximum number of iterations 100 (default) | positive integer

OnlinePhase — Online update flag 'off' (default) | 'on'

Options — Options for controlling iterative algorithm for minimizing fitting criteria [] (default) | structure array returned by statset

Replicates — Number of times to repeat clustering using new initial cluster centroid positions 1 (default) | positive integer

Start — Method for choosing initial cluster centroid positions 'plus' (default) | 'cluster' | 'sample' | 'uniform' | numeric matrix | numeric array

Output Arguments

idx — Cluster indices numeric column vector

C — Cluster centroid locations numeric matrix

sumd — Within-cluster sums of point-to-centroid distances numeric column vector

D — Distances from each point to every centroid numeric matrix

More About

k-Means Clustering

k-means++ Algorithm

Algorithms

References

Extended Capabilities

Tall Arrays Calculate with arrays that have more rows than fit in memory.

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

Automatic Parallel Support Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

GPU Arrays Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Version History

See Also

Topics

External Websites

`X` — Data
numeric matrix

`k` — Number of clusters
positive integer

`Display` — Level of output to display
`'off'` (default) | `'final'` | `'iter'`

`Distance` — Distance metric
`'sqeuclidean'` (default) | `'cityblock'` | `'cosine'` | `'correlation'` | `'hamming'`

`EmptyAction` — Action to take if cluster loses all member observations
`'singleton'` (default) | `'error'` | `'drop'`

`MaxIter` — Maximum number of iterations
`100` (default) | positive integer

`OnlinePhase` — Online update flag
`'off'` (default) | `'on'`

`Options` — Options for controlling iterative algorithm for minimizing fitting criteria
`[]` (default) | structure array returned by `statset`

`Replicates` — Number of times to repeat clustering using new initial cluster centroid positions
`1` (default) | positive integer

`Start` — Method for choosing initial cluster centroid positions
`'plus'` (default) | `'cluster'` | `'sample'` | `'uniform'` | numeric matrix | numeric array

`idx` — Cluster indices
numeric column vector

`C` — Cluster centroid locations
numeric matrix

`sumd` — Within-cluster sums of point-to-centroid distances
numeric column vector

`D` — Distances from each point to every centroid
numeric matrix

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.