silhouette
Silhouette plot
Syntax
Description
silhouette(
accepts one or more additional distance metric parameter values when you specify
X,clust,Distance,DistParameter)Distance as a custom distance function handle
@ that accepts the additional
parameter values.distfun
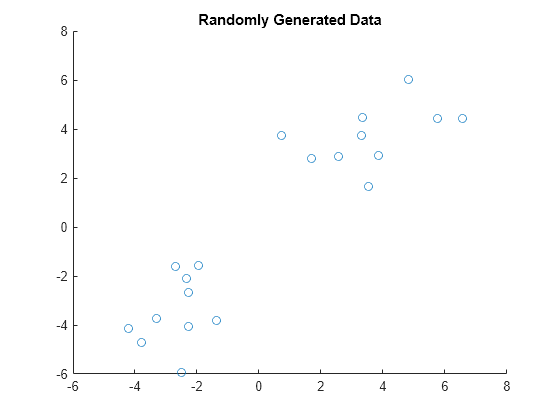
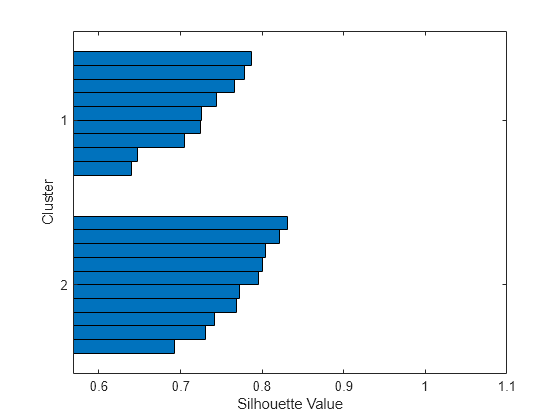
Examples
Input Arguments
Output Arguments
More About
References
[1] Kaufman L., and P. J. Rousseeuw. Finding Groups in Data: An Introduction to Cluster Analysis. Hoboken, NJ: John Wiley & Sons, Inc., 1990.
Version History
Introduced before R2006a