rangesearch

Find all neighbors within specified distance using searcher object

Syntax

Idx = rangesearch(Mdl,Y,r)

Idx = rangesearch(Mdl,Y,r,Name,Value)

[Idx,D]
= rangesearch(___)

Description

Idx = rangesearch(Mdl,Y,r) searches for all neighbors (i.e., points, rows, or observations) in Mdl.X within radius r of each point (i.e., row or observation) in the query data Y using an exhaustive search or a Kd-tree. rangesearch returns Idx, which is a column vector of the indices of Mdl.X within r units.

example

Idx = rangesearch(Mdl,Y,r,Name,Value) returns the indices of the observation in Mdl.X within radius r of each observation in Y with additional options specified by one or more Name,Value pair arguments. For example, you can specify to use a different distance metric than is stored in Mdl.Distance or a different distance metric parameter than is stored in Mdl.DistParameter.

example

[Idx,D] = rangesearch(___) additionally returns the matrix D using any of the input arguments in the previous syntaxes. D contains the distances between the observations in Mdl.X within radius r of each observation in Y. By default, the function arranges the columns of D in ascending order by closeness, with respect to the distance metric.

example

Examples

collapse all

Search for Neighbors Within a Radius Using Kd-tree and Exhaustive Search

Open Live Script

rangesearch accepts ExhaustiveSearcher or KDTreeSearcher model objects to search the training data for the nearest neighbors to the query data. An ExhaustiveSearcher model invokes the exhaustive searcher algorithm, and a KDTreeSearcher model defines a Kd-tree, which rangesearch uses to search for nearest neighbors.

Load Fisher's iris data set. Randomly reserve five observations from the data for query data. Focus on the petal dimensions.

load fisheriris
rng(1); % For reproducibility
n = size(meas,1);
idx = randsample(n,5);
X = meas(~ismember(1:n,idx),3:4); % Training data
Y = meas(idx,3:4);                % Query data

Grow a default two-dimensional Kd-tree.

MdlKDT = KDTreeSearcher(X)

MdlKDT = 
  KDTreeSearcher with properties:

       BucketSize: 50
         Distance: 'euclidean'
    DistParameter: []
                X: [145x2 double]

MdlKDT is a KDTreeSearcher model object. You can alter its writable properties using dot notation.

Prepare an exhaustive nearest neighbor searcher.

MdlES = ExhaustiveSearcher(X)

MdlES = 
  ExhaustiveSearcher with properties:

         Distance: 'euclidean'
    DistParameter: []
                X: [145x2 double]

MdlES is an ExhaustiveSearcher model object. It contains the options, such as the distance metric, to use to find nearest neighbors.

Alternatively, you can grow a Kd-tree or prepare an exhaustive nearest neighbor searcher using createns.

Search training data for the nearest neighbor indices that correspond to each query observation that are within a 0.5 cm radius. Conduct both types of searches and use the default settings.

r = 0.15; % Search radius
IdxKDT = rangesearch(MdlKDT,Y,r);
IdxES = rangesearch(MdlES,Y,r);
[IdxKDT IdxES]

ans=5×2 cell array
    {[ 1 4 8 27 32 45 47 2 35 37 41 6 17 12 36 3 7 10 26 33 38 46 39 40 19 9 31]}    {[ 1 4 8 27 32 45 47 2 35 37 41 6 17 12 36 3 7 10 26 33 38 46 39 40 19 9 31]}
    {[                                                                       13]}    {[                                                                       13]}
    {[6 17 39 40 1 4 8 27 32 45 47 19 2 35 37 41 16 3 7 10 26 33 38 46 15 21 30]}    {[6 17 39 40 1 4 8 27 32 45 47 19 2 35 37 41 16 3 7 10 26 33 38 46 15 21 30]}
    {[                                                                    64 66]}    {[                                                                    64 66]}
    {1x0 double                                                                 }    {1x0 double                                                                 }

IdxKDT and IdxES are cell arrays of vectors corresponding to the indices of X that are within 0.15 cm of the observations in Y. Each row of the index matrices corresponds to a query observation.

Compare the results between the methods.

cellfun(@isequal,IdxKDT,IdxES)

ans = 5x1 logical array

   1
   1
   1
   1
   1

In this case, the results are the same.

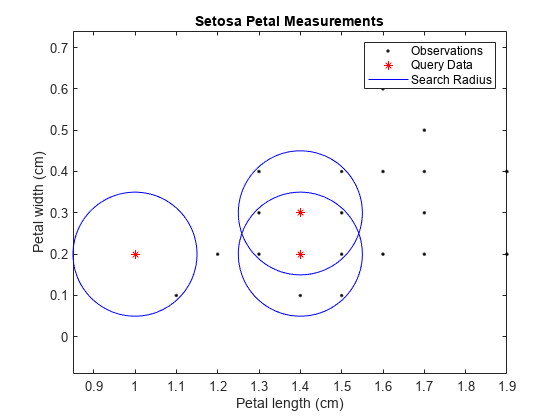
Plot the results for the setosa irises.

setosaIdx = strcmp(species(~ismember(1:n,idx)),'setosa');
XSetosa = X(setosaIdx,:);
ySetosaIdx = strcmp(species(idx),'setosa');
YSetosa = Y(ySetosaIdx,:);

figure;
plot(XSetosa(:,1),XSetosa(:,2),'.k');
hold on;
plot(YSetosa(:,1),YSetosa(:,2),'*r');
for j = 1:sum(ySetosaIdx)
    c = YSetosa(j,:);
    circleFun = @(x1,x2)r^2 - (x1 - c(1)).^2 - (x2 - c(2)).^2;
    fimplicit(circleFun,[c(1) + [-1 1]*r, c(2) + [-1 1]*r],'b-')
end
xlabel 'Petal length (cm)';
ylabel 'Petal width (cm)';
title 'Setosa Petal Measurements';
legend('Observations','Query Data','Search Radius');
axis equal
hold off

Figure contains an axes object. The axes object with title Setosa Petal Measurements, xlabel Petal length (cm), ylabel Petal width (cm) contains 5 objects of type line, implicitfunctionline. One or more of the lines displays its values using only markers These objects represent Observations, Query Data, Search Radius.

Search for Neighbors Within a Radius Using the Mahalanobis Distance

Open Live Script

Load Fisher's iris data set.

load fisheriris

Remove five irises randomly from the predictor data to use as a query set.

rng(1);                     % For reproducibility
n = size(meas,1);           % Sample size
qIdx = randsample(n,5);     % Indices of query data
X = meas(~ismember(1:n,qIdx),:);
Y = meas(qIdx,:);

Prepare a default exhaustive nearest neighbor searcher.

Mdl = ExhaustiveSearcher(X)

Mdl = 
  ExhaustiveSearcher with properties:

         Distance: 'euclidean'
    DistParameter: []
                X: [145x4 double]

Mdl is an ExhaustiveSearcher model.

Find the indices of the training data (X) that are within 0.15 cm of each point in the query data (Y). Specify that the distances are with respect to the Mahalanobis metric.

r = 1;
Idx = rangesearch(Mdl,Y,r,'Distance','mahalanobis')

Idx=5×1 cell array
    {[26 38 7 17 47 4 27 46 25 10 39 20 21 2 33]}
    {[                             6 21 25 4 19]}
    {[                          1 34 33 22 24 2]}
    {[                                       84]}
    {[                                       69]}

Idx{3}

ans = 1×6

     1    34    33    22    24     2

Each cell of Idx corresponds to a query data observation and contains in X a vector of indices of the neighbors within 0.15cm of the query data. rangesearch arranges the indices in ascending order by distance. For example, using the Mahalanobis distance, the second nearest neighbor of Y(3,:) is X(34,:).

Compute Distances of Neighbors Within a Radius

Open Live Script

Load Fisher's iris data set.

load fisheriris

Remove five irises randomly from the predictor data to use as a query set.

rng(4);                     % For reproducibility
n = size(meas,1);           % Sample size
qIdx = randsample(n,5);     % Indices of query data
X = meas(~ismember(1:n,qIdx),:);
Y = meas(qIdx,:);

Grow a four-dimensional Kd-tree using the training data. Specify to use the Minkowski distance for finding nearest neighbors.

Mdl = KDTreeSearcher(X);

Mdl is a KDTreeSearcher model. By default, the distance metric for finding nearest neighbors is the Euclidean metric.

Find the indices of the training data (X) that are within 0.5 cm from each point in the query data (Y).

r = 0.5;
[Idx,D] = rangesearch(Mdl,Y,r);

Idx and D are five-element cell arrays of vectors. The vector values in Idx are the indices in X. The X indices represent the observations that are within 0.5 cm of the query data, Y. D contains the distances that correspond to the observations.

Display the results for query observation 3.

Idx{3}

ans = 1×2

   127   122

D{3}

ans = 1×2

    0.2646    0.4359

The closest observation to Y(3,:) is X(127,:), which is 0.2646 cm away. The next closest is X(122,:), which is 0.4359 cm away. All other observations are greater than 0.5 cm away from Y(5,:).

Input Arguments

collapse all

`Mdl` — Nearest neighbor searcher
`ExhaustiveSearcher` model object | `KDTreeSearcher` model object | `hnswSearcher` model object

Nearest neighbor searcher, specified as an ExhaustiveSearcher, KDTreeSearcher, or hnswSearcher model object.

If Mdl is an ExhaustiveSearcher model, then rangesearch searches for nearest neighbors using an exhaustive search. If Mdl is a KDTreeSearcher model, rangesearch uses the grown Kd-tree to search for nearest neighbors. If Mdl is an hnswSearcher model, rangesearch uses the Hierarchical Navigable Small Worlds approximate neighbor search algorithm. For descriptions, see k-Nearest Neighbor Search and Radius Search.

`Y` — Query data
numeric matrix

Query data, specified as a numeric matrix.

Y is an m-by-K matrix. Rows of Y correspond to observations (i.e., examples), and columns correspond to predictors (i.e., variables or features). Y must have the same number of columns as the training data stored in Mdl.X.

Data Types: single | double

`r` — Search radius
nonnegative scalar

Search radius around each point in the query data, specified as a nonnegative scalar.

rangesearch finds all observations in Mdl.X that are within distance r of each observation in Y. The property Mdl.Distance stores the distance.

Data Types: single | double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Distance','minkowski','P',3 specifies to find all observations in Mdl.X within distance r of each observation in Y, using the Minkowski distance metric with exponent 3.

For Both Nearest Neighbor Searchers

collapse all

`Distance` — Distance metric
`Mdl.Distance` (default) | `'cityblock'` | `'euclidean'` | `'mahalanobis'` | `'minkowski'` | `'seuclidean'` | function handle | ...

Distance metric used to find neighbors of the training data to the query observations, specified as one of the values in this table or function handle.

For all types of nearest neighbor searchers, rangesearch supports these distance metrics.

Value	Description
`'chebychev'`	Chebychev distance (maximum coordinate difference)
`'cityblock'`	City block distance
`'euclidean'`	Euclidean distance
`'minkowski'`	Minkowski distance. The default exponent is 2. To specify a different exponent, use the `'P'` name-value argument.

If Mdl is an ExhaustiveSearcher model object, then rangesearch also supports these distance metrics.

Value	Description
`'correlation'`	One minus the sample linear correlation between observations (treated as sequences of values)
`'cosine'`	One minus the cosine of the included angle between observations (treated as row vectors)
`'fasteuclidean'`	Euclidean distance computed by using an alternative algorithm that saves time when the number of predictors is at least 10. In some cases, this faster algorithm can reduce accuracy. This distance metric is available only when `NSMethod` is `'exhaustive'`. Algorithms starting with `'fast'` do not support sparse data. For details, see Algorithms.
`'fastseuclidean'`	Standardized Euclidean distance computed by using an alternative algorithm that saves time when the number of predictors is at least 10. In some cases, this faster algorithm can reduce accuracy. This distance metric is available only when `NSMethod` is `'exhaustive'`. Algorithms starting with `'fast'` do not support sparse data. For details, see Algorithms.
`'hamming'`	Hamming distance, which is the percentage of coordinates that differ
`'jaccard'`	One minus the Jaccard coefficient, which is the percentage of nonzero coordinates that differ
`'mahalanobis'`	Mahalanobis distance, computed using a positive definite covariance matrix. To change the value of the covariance matrix, use the `'Cov'` name-value argument.
`'seuclidean'`	Standardized Euclidean distance. Each coordinate difference between the rows in `X` and the query matrix `Y` is scaled by dividing by the corresponding element of the standard deviation computed from `X`. To specify a different scaling, use the `'Scale'` name-value argument.
`'spearman'`	One minus the sample Spearman's rank correlation between observations (treated as sequences of values)

If Mdl is an hnswSearcher model object, rangesearch supports all the distances in the ExhaustiveSearcher table except for those beginning with fast: "fasteuclidean" and "fastseuclidean".

If Mdl is an ExhaustiveSearcher model object, then you can also specify a function handle for a custom distance metric by using @ (for example, @distfun). The custom distance function must:

Have the form function D2 = distfun(ZI,ZJ).
Take as arguments:
- A 1-by-K vector ZI containing a single row from Mdl.X or Y, where K is the number of columns of Mdl.X.
- An m-by-K matrix ZJ containing multiple rows of Mdl.X or Y, where m is a positive integer.
Return an m-by-1 vector of distances D2, where D2(j) is the distance between the observations ZI and ZJ(j,:).

For more details, see Distance Metrics.

Example: 'Distance','minkowski'

Data Types: char | string | function_handle

`P` — Exponent for Minkowski distance metric
`2` (default) | positive scalar

Exponent for the Minkowski distance metric, specified as a positive scalar. This argument is valid only when Distance is "minkowski".

The value of P sets the value of the DistParameter property in the model object.

Example: P=3

Data Types: single | double

`SortIndices` — Flag to sort returned indices according to distance
`true` (`1`) (default) | `false` (`0`)

Flag to sort returned indices according to distance, specified as the comma-separated pair consisting of 'SortIndices' and either true (1) or false (0).

For faster performance when Y contains many observations that have many nearest points, you can set SortIndices to false. In this case, rangesearch returns the indices of the nearest points in no particular order. When SortIndices is true, the function arranges the indices of the nearest points in ascending order by distance.

Example: 'SortIndices',false

Data Types: logical

For Exhaustive Nearest Neighbor Searchers

collapse all

`Cov` — Covariance matrix for Mahalanobis distance metric
`cov(Mdl.X,'omitrows')` (default) | positive definite matrix

Covariance matrix for the Mahalanobis distance metric, specified as the comma-separated pair consisting of 'Cov' and a positive definite matrix. Cov is a K-by-K matrix, where K is the number of columns of Mdl.X. If you specify Cov and do not specify 'Distance','mahalanobis', then rangesearch returns an error message.

Example: 'Cov',eye(3)

Data Types: single | double

`Scale` — Scale parameter value for standardized Euclidean distance metric
`std(Mdl.X,'omitnan')` (default) | nonnegative numeric vector

Scale parameter value for the standardized Euclidean distance metric, specified as the comma-separated pair consisting of 'Scale' and a nonnegative numeric vector. Scale has length K, where K is the number of columns of Mdl.X.

The software scales each difference between the training and query data using the corresponding element of Scale. If you specify Scale and do not specify 'Distance','seuclidean', then rangesearch returns an error message.

Example: 'Scale',quantile(Mdl.X,0.75) - quantile(Mdl.X,0.25)

Data Types: single | double

Note

If you specify 'Distance', 'Cov', 'P', or 'Scale', then Mdl.Distance and Mdl.DistParameter do not change value.

Output Arguments

collapse all

`Idx` — Training data indices of nearest neighbors
cell array of numeric vectors

Training data indices of nearest neighbors, returned as a cell array of numeric vectors.

Idx is an m-by-1 cell array such that cell j (Idx{j}) contains an m_j-dimensional vector of indices of the observations in Mdl.X that are within r units to the query observation Y(j,:). If SortIndices is true, then rangesearch arranges the elements of the vectors in ascending order by distance.

`D` — Distances of nearest neighbors to the query data
cell array of numeric vectors

Distances of the neighbors to the query data, returned as a numeric matrix or cell array of numeric vectors.

D is an m-by-1 cell array such that cell j (D{j}) contains an m_j-dimensional vector of the distances that the observations in Mdl.X are from the query observation Y(j,:). All elements of the vector are less than r. If SortIndices is true, then rangesearch arranges the elements of the vectors in ascending order.

Tips

knnsearch finds the k (positive integer) points in Mdl.X that are k-nearest for each Y point. In contrast, rangesearch finds all the points in Mdl.X that are within distance r (positive scalar) of each Y point.

Alternative Functionality

rangesearch is an object function that requires an ExhaustiveSearcher or a KDTreeSearcher model object, query data, and a distance. Under equivalent conditions, rangesearch returns the same results as rangesearch when you specify the name-value pair argument 'NSMethod','exhaustive' or 'NSMethod','kdtree', respectively.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

This table contains notes about the arguments of rangesearch. Arguments not included in this table are fully supported.

Argument	Notes and Limitations
`Mdl`	There are two ways to use `Mdl` in code generation. For an example, see Code Generation for Nearest Neighbor Searcher. Use `saveLearnerForCoder`, `loadLearnerForCoder`, and `codegen` (MATLAB Coder) to generate code for the `rangesearch` function. Save a trained model by using `saveLearnerForCoder`. Define an entry-point function that loads the saved model by using `loadLearnerForCoder` and calls the `rangesearch` function. Then use `codegen` to generate code for the entry-point function. Include `coder.Constant(Mdl)` in the `-args` value of `codegen` (MATLAB Coder). If `Mdl` is a `KDTreeSearcher` object, and the code generation build type is a MEX function, then `codegen` (MATLAB Coder) generates a MEX function using Intel^® Threading Building Blocks (TBB) for parallel computation. Otherwise, `codegen` generates code using `parfor` (MATLAB Coder). MEX function for the kd-tree search algorithm — `codegen` generates an optimized MEX function using Intel TBB for parallel computation on multicore platforms. You can use the MEX function to accelerate MATLAB^® algorithms. For details on Intel TBB, see https://www.intel.com/content/www/us/en/developer/tools/oneapi/onetbb.html. If you generate the MEX function to test the generated code of the `parfor` version, you can disable the usage of Intel TBB. Set the `ExtrinsicCalls` property of the MEX configuration object to `false`. For details, see `coder.MexCodeConfig` (MATLAB Coder). MEX function for the exhaustive search algorithm and standalone C/C++ code for both algorithms — The generated code of `rangesearch` uses `parfor` (MATLAB Coder) to create loops that run in parallel on supported shared-memory multicore platforms in the generated code. If your compiler does not support the Open Multiprocessing (OpenMP) application interface or you disable OpenMP library, MATLAB Coder™ treats the `parfor`-loops as `for`-loops. To find supported compilers, see Supported Compilers. To disable OpenMP library, set the `EnableOpenMP` property of the configuration object to `false`. For details, see `coder.CodeConfig` (MATLAB Coder).
`'Distance'`	Cannot be a custom distance function. Must be a compile-time constant; its value cannot change in the generated code.
`'SortIndices'`	Not supported. The output arguments are always sorted.
Name-value pair arguments	Names in name-value arguments must be compile-time constants. For example, to allow a user-defined exponent for the Minkowski distance in the generated code, include `{coder.Constant('Distance'),coder.Constant('Minkowski'),coder.Constant('P'),0}` in the `-args` value of `codegen` (MATLAB Coder).
`Idx`	The sorted order of tied distances in the generated code can be different from the order in MATLAB due to numerical precision. `rangesearch` returns integer-type (`int32`) indices in generated standalone C/C++ code. Therefore, the function allows for strict single-precision support when you use single-precision inputs. For MEX code generation, the function still returns double-precision indices to match the MATLAB behavior. Before R2020a: `rangesearch` returns double-precision indices in generated standalone C/C++ code.

For more information, see Introduction to Code Generation and Code Generation for Nearest Neighbor Searcher.

Version History

Introduced in R2011b

rangesearch

Syntax

Description

Examples

Search for Neighbors Within a Radius Using Kd-tree and Exhaustive Search

Search for Neighbors Within a Radius Using the Mahalanobis Distance

Compute Distances of Neighbors Within a Radius

Input Arguments

`Mdl` — Nearest neighbor searcher
`ExhaustiveSearcher` model object | `KDTreeSearcher` model object | `hnswSearcher` model object

`Y` — Query data
numeric matrix

`r` — Search radius
nonnegative scalar

Name-Value Arguments

`Distance` — Distance metric
`Mdl.Distance` (default) | `'cityblock'` | `'euclidean'` | `'mahalanobis'` | `'minkowski'` | `'seuclidean'` | function handle | ...

`P` — Exponent for Minkowski distance metric
`2` (default) | positive scalar

`SortIndices` — Flag to sort returned indices according to distance
`true` (`1`) (default) | `false` (`0`)

`Cov` — Covariance matrix for Mahalanobis distance metric
`cov(Mdl.X,'omitrows')` (default) | positive definite matrix

`Scale` — Scale parameter value for standardized Euclidean distance metric
`std(Mdl.X,'omitnan')` (default) | nonnegative numeric vector

Output Arguments

`Idx` — Training data indices of nearest neighbors
cell array of numeric vectors

`D` — Distances of nearest neighbors to the query data
cell array of numeric vectors

Tips

Alternative Functionality

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

See Also

Topics

rangesearch

Syntax

Description

Examples

Search for Neighbors Within a Radius Using Kd-tree and Exhaustive Search

Search for Neighbors Within a Radius Using the Mahalanobis Distance

Compute Distances of Neighbors Within a Radius

Input Arguments

Mdl — Nearest neighbor searcher ExhaustiveSearcher model object | KDTreeSearcher model object | hnswSearcher model object

Y — Query data numeric matrix

r — Search radius nonnegative scalar

Name-Value Arguments

Distance — Distance metric Mdl.Distance (default) | 'cityblock' | 'euclidean' | 'mahalanobis' | 'minkowski' | 'seuclidean' | function handle | ...

P — Exponent for Minkowski distance metric 2 (default) | positive scalar

SortIndices — Flag to sort returned indices according to distance true (1) (default) | false (0)

Cov — Covariance matrix for Mahalanobis distance metric cov(Mdl.X,'omitrows') (default) | positive definite matrix

Scale — Scale parameter value for standardized Euclidean distance metric std(Mdl.X,'omitnan') (default) | nonnegative numeric vector

Output Arguments

Idx — Training data indices of nearest neighbors cell array of numeric vectors

D — Distances of nearest neighbors to the query data cell array of numeric vectors

Tips

Alternative Functionality

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

Version History

See Also

Topics

`Mdl` — Nearest neighbor searcher
`ExhaustiveSearcher` model object | `KDTreeSearcher` model object | `hnswSearcher` model object

`Y` — Query data
numeric matrix

`r` — Search radius
nonnegative scalar

`Distance` — Distance metric
`Mdl.Distance` (default) | `'cityblock'` | `'euclidean'` | `'mahalanobis'` | `'minkowski'` | `'seuclidean'` | function handle | ...

`P` — Exponent for Minkowski distance metric
`2` (default) | positive scalar

`SortIndices` — Flag to sort returned indices according to distance
`true` (`1`) (default) | `false` (`0`)

`Cov` — Covariance matrix for Mahalanobis distance metric
`cov(Mdl.X,'omitrows')` (default) | positive definite matrix

`Scale` — Scale parameter value for standardized Euclidean distance metric
`std(Mdl.X,'omitnan')` (default) | nonnegative numeric vector

`Idx` — Training data indices of nearest neighbors
cell array of numeric vectors

`D` — Distances of nearest neighbors to the query data
cell array of numeric vectors

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.