Main Content

fscnca

Feature selection using neighborhood component analysis for classification

collapse all in page

Syntax

mdl = fscnca(Tbl,ResponseVarName)
mdl = fscnca(Tbl,formula)
mdl = fscnca(Tbl,Y)
mdl = fscnca(X,Y)
mdl = fscnca(X,Y,Name,Value)

Description

fscnca performs feature selection using neighborhood component analysis (NCA) for classification.

To perform NCA-based feature selection for regression, see fsrnca.

mdl = fscnca(Tbl,ResponseVarName) returns the NCA feature selection model for classification using the sample data contained in the table Tbl. ResponseVarName is the name of the variable in Tbl that contains the class labels.

fscnca learns the feature weights by using a diagonal adaptation of NCA with regularization.

mdl = fscnca(Tbl,formula) returns the NCA feature selection model for classification using the sample data contained in the table Tbl. formula is an explanatory model of the response and a subset of the predictor variables in the table Tbl used to fit mdl.

mdl = fscnca(Tbl,Y) returns the NCA feature selection model for classification using the predictors in the table Tbl and responses in Y.

mdl = fscnca(X,Y) returns the NCA feature selection model for classification using the predictors in matrix X and responses in Y.

example

mdl = fscnca(X,Y,Name,Value) specifies additional options using one or more name-value arguments. For example, you can specify the method for fitting the model, the regularization parameter, and the initial feature weights.

example

Examples

collapse all

Open Live Script

Generate toy data where the response variable depends on the 3rd, 9th, and 15th predictors.

rng(0,'twister'); % For reproducibility
N = 100;
X = rand(N,20);
y = -ones(N,1);
y(X(:,3).*X(:,9)./X(:,15) < 0.4) = 1;

Fit the neighborhood component analysis model for classification.

mdl = fscnca(X,y,'Solver','sgd','Verbose',1);
 o Tuning initial learning rate: NumTuningIterations = 20, TuningSubsetSize = 100

|===============================================|
|    TUNING    | TUNING SUBSET |    LEARNING    |
|     ITER     |   FUN VALUE   |      RATE      |
|===============================================|
|            1 | -3.755936e-01 |   2.000000e-01 |
|            2 | -3.950971e-01 |   4.000000e-01 |
|            3 | -4.311848e-01 |   8.000000e-01 |
|            4 | -4.903195e-01 |   1.600000e+00 |
|            5 | -5.630190e-01 |   3.200000e+00 |
|            6 | -6.166993e-01 |   6.400000e+00 |
|            7 | -6.255669e-01 |   1.280000e+01 |
|            8 | -6.255669e-01 |   1.280000e+01 |
|            9 | -6.255669e-01 |   1.280000e+01 |
|           10 | -6.255669e-01 |   1.280000e+01 |
|           11 | -6.255669e-01 |   1.280000e+01 |
|           12 | -6.255669e-01 |   1.280000e+01 |
|           13 | -6.255669e-01 |   1.280000e+01 |
|           14 | -6.279210e-01 |   2.560000e+01 |
|           15 | -6.279210e-01 |   2.560000e+01 |
|           16 | -6.279210e-01 |   2.560000e+01 |
|           17 | -6.279210e-01 |   2.560000e+01 |
|           18 | -6.279210e-01 |   2.560000e+01 |
|           19 | -6.279210e-01 |   2.560000e+01 |
|           20 | -6.279210e-01 |   2.560000e+01 |

 o Solver = SGD, MiniBatchSize = 10, PassLimit = 5

|==========================================================================================|
|   PASS   |     ITER     | AVG MINIBATCH | AVG MINIBATCH |   NORM STEP   |    LEARNING    |
|          |              |   FUN VALUE   |   NORM GRAD   |               |      RATE      |
|==========================================================================================|
|        0 |            9 | -5.658450e-01 |  4.492407e-02 |  9.290605e-01 |   2.560000e+01 |
|        1 |           19 | -6.131382e-01 |  4.923625e-02 |  7.421541e-01 |   1.280000e+01 |
|        2 |           29 | -6.225056e-01 |  3.738784e-02 |  3.277588e-01 |   8.533333e+00 |
|        3 |           39 | -6.233366e-01 |  4.947901e-02 |  5.431133e-01 |   6.400000e+00 |
|        4 |           49 | -6.238576e-01 |  3.445763e-02 |  2.946188e-01 |   5.120000e+00 |

         Two norm of the final step = 2.946e-01
Relative two norm of the final step = 6.588e-02, TolX = 1.000e-06
EXIT: Iteration or pass limit reached.

Plot the selected features. The weights of the irrelevant features should be close to zero.

figure()
plot(mdl.FeatureWeights,'ro')
grid on
xlabel('Feature index')
ylabel('Feature weight')

Figure contains an axes object. The axes object with xlabel Feature index, ylabel Feature weight contains a line object which displays its values using only markers.

fscnca correctly detects the relevant features.

Open Live Script

Load and partition the ovarian cancer data set, and determine if feature selection is necessary. Fit the model, plot the feature weights, and then classify observations using the selected features. 

load ovariancancer; 
whos
  Name        Size                Bytes  Class     Attributes

  grp       216x1                 28512  cell                
  obs       216x4000            3456000  single

The obs variable consists of 216 observations with 4000 features. Each element in grp defines the group to which the corresponding row of obs belongs.

Use cvpartition to divide the data into a training set of size 160 and a test set of size 56. Both the training set and the test set have roughly the same group proportions as in grp.

rng(1,"twister"); % For reproducibility
cvp = cvpartition(grp,Holdout=56)
cvp = 
Hold-out cross validation partition
   NumObservations: 216
       NumTestSets: 1
         TrainSize: 160
          TestSize: 56
          IsCustom: 0

Xtrain = obs(cvp.training,:);
ytrain = grp(cvp.training,:);
Xtest  = obs(cvp.test,:);
ytest  = grp(cvp.test,:);

To determine if feature selection is necessary, first compute the generalization error without fitting. 

nca = fscnca(Xtrain,ytrain,FitMethod="none");
loss(nca,Xtest,ytest)
ans = 
0.0893

The software computes the generalization error of the neighborhood component analysis (NCA) feature selection model using the initial feature weights (in this case, the default feature weights) provided by fscnca.

Fit the NCA model without the regularization parameter (that is, Lambda = 0).

nca = fscnca(Xtrain,ytrain,FitMethod="exact",Lambda=0,...
      Solver="sgd",Standardize=true);
loss(nca,Xtest,ytest)
ans = 
0.0714

The improvement in the loss value suggests that feature selection is worthwhile. Tuning the regularization parameter (Lambda value) usually improves the results.

Tuning the regularization parameter for the NCA model means finding the Lambda value that produces the minimum classification loss. To tune the parameter using five-fold cross-validation:

1. Partition the training data into five folds and extract the number of validation (test) sets. For each fold, cvpartition assigns four-fifths of the data as a training set, and one-fifth of the data as a test set.

cvp = cvpartition(ytrain,KFold=5);
numvalidsets = cvp.NumTestSets;

Assign Lambda values and create an array to store the loss function values.

n = length(ytrain);
lambdavals = linspace(0,20,20)/n;
lossvals = zeros(length(lambdavals),numvalidsets);

2. Train the NCA model for each Lambda value, using the training set in each fold.

3. Compute the classification loss for the corresponding test set in the fold using the NCA model. Record the loss value.

4. Repeat this process for all folds and all Lambda values.

for i = 1:length(lambdavals)
    for k = 1:numvalidsets
        X = Xtrain(cvp.training(k),:);
        y = ytrain(cvp.training(k),:);
        Xvalid = Xtrain(cvp.test(k),:);
        yvalid = ytrain(cvp.test(k),:);

        nca = fscnca(X,y,FitMethod="exact", ...
             Solver="sgd",Lambda=lambdavals(i), ...
             IterationLimit=30,GradientTolerance=1e-4, ...
             Standardize=true);
                  
        lossvals(i,k) = loss(nca,Xvalid,yvalid,LossFunction="classiferror");
    end
end

Compute the average loss obtained from the folds for each Lambda value.

meanloss = mean(lossvals,2);

Plot the average loss values versus the Lambda values.

figure()
plot(lambdavals,meanloss,"ro-")
xlabel("Lambda")
ylabel("Loss (MSE)")
grid on

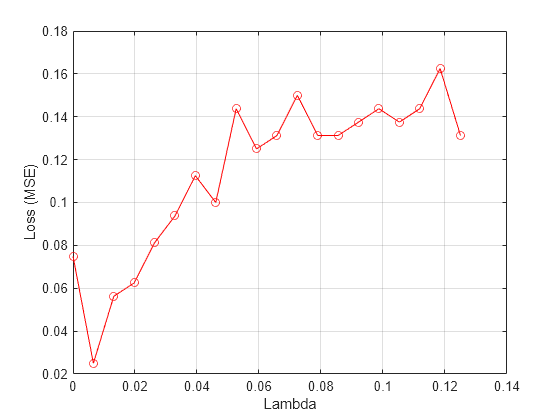
Figure contains an axes object. The axes object with xlabel Lambda, ylabel Loss (MSE) contains an object of type line.

Find the best Lambda value that corresponds to the minimum average loss.

[~,idx] = min(meanloss) % Find the index
idx = 
2

bestlambda = lambdavals(idx) % Find the best Lambda value
bestlambda = 
0.0066

bestloss = meanloss(idx)
bestloss = 
0.0312

Fit the NCA model on all the data using the best Lambda value. Use the solver sgd and standardize the predictor values. 

nca = fscnca(Xtrain,ytrain,FitMethod="exact",Solver="sgd",...
    Lambda=bestlambda,Standardize=true,Verbose=1);
 o Tuning initial learning rate: NumTuningIterations = 20, TuningSubsetSize = 100

|===============================================|
|    TUNING    | TUNING SUBSET |    LEARNING    |
|     ITER     |   FUN VALUE   |      RATE      |
|===============================================|
|            1 |  2.403497e+01 |   2.000000e-01 |
|            2 |  2.275050e+01 |   4.000000e-01 |
|            3 |  2.036845e+01 |   8.000000e-01 |
|            4 |  1.627647e+01 |   1.600000e+00 |
|            5 |  1.023512e+01 |   3.200000e+00 |
|            6 |  3.864283e+00 |   6.400000e+00 |
|            7 |  4.743816e-01 |   1.280000e+01 |
|            8 | -7.260138e-01 |   2.560000e+01 |
|            9 | -7.260138e-01 |   2.560000e+01 |
|           10 | -7.260138e-01 |   2.560000e+01 |
|           11 | -7.260138e-01 |   2.560000e+01 |
|           12 | -7.260138e-01 |   2.560000e+01 |
|           13 | -7.260138e-01 |   2.560000e+01 |
|           14 | -7.260138e-01 |   2.560000e+01 |
|           15 | -7.260138e-01 |   2.560000e+01 |
|           16 | -7.260138e-01 |   2.560000e+01 |
|           17 | -7.260138e-01 |   2.560000e+01 |
|           18 | -7.260138e-01 |   2.560000e+01 |
|           19 | -7.260138e-01 |   2.560000e+01 |
|           20 | -7.260138e-01 |   2.560000e+01 |

 o Solver = SGD, MiniBatchSize = 10, PassLimit = 5

|==========================================================================================|
|   PASS   |     ITER     | AVG MINIBATCH | AVG MINIBATCH |   NORM STEP   |    LEARNING    |
|          |              |   FUN VALUE   |   NORM GRAD   |               |      RATE      |
|==========================================================================================|
|        0 |            9 |  4.016078e+00 |  2.835465e-02 |  5.395984e+00 |   2.560000e+01 |
|        1 |           19 | -6.726156e-01 |  6.111354e-02 |  5.021138e-01 |   1.280000e+01 |
|        1 |           29 | -8.316555e-01 |  4.024186e-02 |  1.196031e+00 |   1.280000e+01 |
|        2 |           39 | -8.838656e-01 |  2.333416e-02 |  1.225834e-01 |   8.533333e+00 |
|        3 |           49 | -8.669034e-01 |  3.413162e-02 |  3.421902e-01 |   6.400000e+00 |
|        3 |           59 | -8.906936e-01 |  1.946295e-02 |  2.232511e-01 |   6.400000e+00 |
|        4 |           69 | -8.778630e-01 |  3.561290e-02 |  3.290645e-01 |   5.120000e+00 |
|        4 |           79 | -8.857135e-01 |  2.516638e-02 |  3.902979e-01 |   5.120000e+00 |

         Two norm of the final step = 3.903e-01
Relative two norm of the final step = 6.171e-03, TolX = 1.000e-06
EXIT: Iteration or pass limit reached.

Plot the feature weights.

figure()
plot(nca.FeatureWeights,"ro")
xlabel("Feature Index")
ylabel("Feature Weight")
grid on

Figure contains an axes object. The axes object with xlabel Feature Index, ylabel Feature Weight contains a line object which displays its values using only markers.

Most of the feature weights are very close to zero, which means that they are irrelevant. Some features have much higher feature weight values. In this case, to select a reasonable number of predictors, specify a threshold of 0.02 times the maximum feature weight value.

selidx = find(nca.FeatureWeights > 0.02*max(1,max(nca.FeatureWeights)))
selidx = 72×1

   565
   611
   654
   681
   737
   743
   744
   750
   754
   839
      ⋮

Compute the classification loss using the test set.

loss(nca,Xtest,ytest)
ans = 
0.0179

Extract the features with feature weights greater than the specified threshold value from the training data. 

features = Xtrain(:,selidx);

Apply a support vector machine classifier to the reduced training set using the selected features.

svmMdl = fitcsvm(features,ytrain);

Evaluate the accuracy of the trained classifier on the test data, which has not been used for feature selection. 

loss(svmMdl,Xtest(:,selidx),ytest)
ans = single

0

Input Arguments

collapse all

Sample data used to train the model, specified as a table. Each row of Tbl corresponds to one observation, and each column corresponds to one predictor variable.

Data Types: table

Response variable name, specified as the name of a variable in Tbl. The remaining variables in the table are predictors.

Data Types: char | string

Predictor variable values, specified as an n-by-p matrix, where n is the number of observations and p is the number of predictor variables.

Data Types: single | double

Explanatory model of the response variable and a subset of the predictor variables, specified as a string or a character vector in the form "Y~x1+x2+x3". In this form, Y represents the response variable, and x1, x2, and x3 represent the predictor variables.

To specify a subset of variables in Tbl as predictors for training the model, use a formula. If you specify a formula, then the software does not use any variables in Tbl that do not appear in formula.

The variable names in the formula must be both variable names in Tbl (Tbl.Properties.VariableNames) and valid MATLAB® identifiers. You can verify the variable names in Tbl by using the isvarname function. If the variable names are not valid, then you can convert them by using the matlab.lang.makeValidName function.

Data Types: char | string

Class labels, specified as a categorical array, logical vector, numeric vector, string array, cell array of character vectors of length n, or character matrix with n rows. n is the number of observations. Element i or row i of Y is the class label corresponding to row i of X (observation i).

Data Types: single | double | logical | char | string | cell | categorical

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Solver','sgd','Weights',W,'Lambda',0.0003 specifies the solver as the stochastic gradient descent, the observation weights as the values in the vector W, and sets the regularization parameter at 0.0003.

Fitting Options

collapse all

Method for fitting the model, specified as the comma-separated pair consisting of 'FitMethod' and one of the following:

  • 'exact' — Performs fitting using all of the data.

  • 'none' — No fitting. Use this option to evaluate the generalization error of the NCA model using the initial feature weights supplied in the call to fscnca.

  • 'average' — Divides the data into partitions (subsets), fits each partition using the exact method, and returns the average of the feature weights. You can specify the number of partitions using the NumPartitions name-value pair argument.

Example: 'FitMethod','none'

Number of partitions to split the data for using with 'FitMethod','average' option, specified as the comma-separated pair consisting of 'NumPartitions' and an integer value between 2 and n, where n is the number of observations.

Example: 'NumPartitions',15

Data Types: double | single

Regularization parameter to prevent overfitting, specified as the comma-separated pair consisting of 'Lambda' and a nonnegative scalar.

As the number of observations n increases, the chance of overfitting decreases and the required amount of regularization also decreases. See Identify Relevant Features for Classification and Tune Regularization Parameter to Detect Features Using NCA for Classification to learn how to tune the regularization parameter.

Example: 'Lambda',0.002

Data Types: double | single

Width of the kernel, specified as the comma-separated pair consisting of 'LengthScale' and a positive real scalar.

A length scale value of 1 is sensible when all predictors are on the same scale. If the predictors in X are of very different magnitudes, then consider standardizing the predictor values using 'Standardize',true and setting 'LengthScale',1.

Example: 'LengthScale',1.5

Data Types: double | single

Categorical predictors list, specified as one of the values in this table.

ValueDescription
Vector of positive integersEach entry in the vector is an index value corresponding to the column of the predictor data (X) that contains a categorical variable.
Logical vectorA true entry means that the corresponding column of predictor data (X) is a categorical variable.
Character matrixEach row of the matrix is the name of a predictor variable in the table X. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length.
String array or cell array of character vectorsEach element in the array is the name of a predictor variable in the table X. The names must match the entries in PredictorNames.
"all"All predictors are categorical.

By default, if the predictor data is in a table, fscnca assumes that a variable is categorical if it is a logical vector, categorical vector, character array, string array, or cell array of character vectors. If the predictor data is a matrix, fscnca assumes that all predictors are continuous. To identify any other predictors as categorical predictors, specify them by using the CategoricalPredictors name-value argument.

For the identified categorical predictors, fscnca creates dummy variables using two different schemes, depending on whether a categorical variable is unordered or ordered:

  • For an unordered categorical variable, fscnca creates one dummy variable for each level of the categorical variable.

  • For an ordered categorical variable, fscnca creates one less dummy variable than the number of categories. For details, see Automatic Creation of Dummy Variables.

For the table X, categorical predictors can be ordered and unordered. For the matrix X, fscnca treats categorical predictors as unordered.

Example: CategoricalPredictors="all"

Data Types: double | logical | char | string

Predictor variable names, specified as a string array of unique names or cell array of unique character vectors. The functionality of PredictorNames depends on the way you supply the training data.

  • If you supply X as a matrix, then you can use PredictorNames to assign names to the predictor variables in X.

    • The order of the names in PredictorNames must correspond to the predictor order in X. That is, PredictorNames{1} is the name of X(:,1), PredictorNames{2} is the name of X(:,2), and so on. Also, size(X,2) and numel(PredictorNames) must be equal.

    • By default, PredictorNames is {'X1','X2',...}.

  • If you supply X as a table, then you can use PredictorNames to specify which predictor variables to use in training. That is, fscnca uses only the predictor variables in PredictorNames and the response variable during training.

    • PredictorNames must be a subset of X.Properties.VariableNames and cannot include the name of the response variable.

    • By default, PredictorNames contains the names of all predictor variables.

    • Specify the predictors for training using either PredictorNames or a formula string in Y (such as 'y ~ x1 + x2 + x3'), but not both.

Example: "PredictorNames={"SepalLength","SepalWidth","PetalLength","PetalWidth"}

Data Types: string | cell

Response variable name, specified as a character vector or string scalar.

  • If you supply Y, then you can use ResponseName to specify a name for the response variable.

  • If you supply ResponseVarName or formula, then you cannot use ResponseName.

Example: ResponseName="response"

Data Types: char | string

Initial feature weights, specified as an M-by-1 vector of positive numbers, where M is the number of predictor variables after dummy variables are created for categorical variables (for details, see CategoricalPredictors).

The regularized objective function for optimizing feature weights is nonconvex. As a result, using different initial feature weights might give different results. Setting all initial feature weights to 1 generally works well, but in some cases, random initialization using rand(M,1) might give better quality solutions.

For more information about feature weights, see Neighborhood Component Analysis (NCA) Feature Selection.

Data Types: double | single

Observation weights, specified as the comma-separated pair consisting of 'Weights' and an n-by-1 vector of real positive scalars. Use observation weights to specify higher importance of some observations compared to others. The default weights assign equal importance to all observations.

Data Types: double | single

Prior probabilities for each class, specified as the comma-separated pair consisting of 'Prior' and one of the following:

  • 'empirical' — fscnca obtains the prior class probabilities from class frequencies.

  • 'uniform' — fscnca sets all class probabilities equal.

  • Structure with two fields:

    • ClassProbs — Vector of class probabilities. If these are numeric values with a total greater than 1, fsnca normalizes them to add up to 1.

    • ClassNames — Class names corresponding to the class probabilities in ClassProbs.

Example: 'Prior','uniform'

Indicator for standardizing the predictor data, specified as the comma-separated pair consisting of 'Standardize' and either false or true. For more information, see Impact of Standardization.

Example: 'Standardize',true

Data Types: logical

Verbosity level indicator for the convergence summary display, specified as the comma-separated pair consisting of 'Verbose' and one of the following:

  • 0 — No convergence summary

  • 1 — Convergence summary, including norm of gradient and objective function values

  • > 1 — More convergence information, depending on the fitting algorithm

    When using 'minibatch-lbfgs' solver and verbosity level > 1, the convergence information includes iteration the log from intermediate mini-batch LBFGS fits.

Example: 'Verbose',1

Data Types: double | single

Solver type for estimating feature weights, specified as the comma-separated pair consisting of 'Solver' and one of the following:

  • 'lbfgs' — Limited memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) algorithm

  • 'sgd' — Stochastic gradient descent (SGD) algorithm

  • 'minibatch-lbfgs' — Stochastic gradient descent with LBFGS algorithm applied to mini-batches

Default is 'lbfgs' for n ≤ 1000, and 'sgd' for n > 1000.

Example: 'solver','minibatch-lbfgs'

Loss function, specified as the comma-separated pair consisting of 'LossFunction' and one of the following.

  • 'classiferror' — Misclassification error

    l(yi,yj)={1if yi≠yj,0otherwise.

  • @lossfun — Custom loss function handle. A loss function has this form. 

    function L = lossfun(Yu,Yv)
% calculation of loss
...
    Yu is a u-by-1 vector and Yv is a v-by-1 vector. L is a u-by-v matrix of loss values such that L(i,j) is the loss value for Yu(i) and Yv(j).

The objective function for minimization includes the loss function l(yi,yj) as follows:

f(w)=1n∑i=1n∑j=1,j≠inpijl(yi,yj)+λ∑r=1pwr2,

where w is the feature weight vector, n is the number of observations, and p is the number of predictor variables. pij is the probability that xj is the reference point for xi. For details, see NCA Feature Selection for Classification.

Example: 'LossFunction',@lossfun

Memory size, in MB, to use for objective function and gradient computation, specified as the comma-separated pair consisting of 'CacheSize' and an integer.

Example: 'CacheSize',1500MB

Data Types: double | single

LBFGS Options

collapse all

Size of history buffer for Hessian approximation for the 'lbfgs' solver, specified as the comma-separated pair consisting of 'HessianHistorySize' and a positive integer. At each iteration the function uses the most recent HessianHistorySize iterations to build an approximation to the inverse Hessian.

Example: 'HessianHistorySize',20

Data Types: double | single

Initial step size for the 'lbfgs' solver, specified as the comma-separated pair consisting of 'InitialStepSize' and a positive real scalar. By default, the function determines the initial step size automatically.

Data Types: double | single

Line search method, specified as the comma-separated pair consisting of 'LineSearchMethod' and one of the following:

  • 'weakwolfe' — Weak Wolfe line search

  • 'strongwolfe' — Strong Wolfe line search

  • 'backtracking' — Backtracking line search

Example: 'LineSearchMethod','backtracking'

Maximum number of line search iterations, specified as the comma-separated pair consisting of 'MaxLineSearchIterations' and a positive integer.

Example: 'MaxLineSearchIterations',25

Data Types: double | single

Relative convergence tolerance on the gradient norm for solver lbfgs, specified as the comma-separated pair consisting of 'GradientTolerance' and a positive real scalar.

Example: 'GradientTolerance',0.000002

Data Types: double | single

SGD Options

collapse all

Initial learning rate for the 'sgd' solver, specified as the comma-separated pair consisting of 'InitialLearningRate' and a positive real scalar.

When using solver type 'sgd', the learning rate decays over iterations starting with the value specified for 'InitialLearningRate'.

The default 'auto' means that the initial learning rate is determined using experiments on small subsets of data. Use the NumTuningIterations name-value pair argument to specify the number of iterations for automatically tuning the initial learning rate. Use the TuningSubsetSize name-value pair argument to specify the number of observations to use for automatically tuning the initial learning rate.

For solver type 'minibatch-lbfgs', you can set 'InitialLearningRate' to a very high value. In this case, the function applies LBFGS to each mini-batch separately with initial feature weights from the previous mini-batch.

To make sure the chosen initial learning rate decreases the objective value with each iteration, plot the Iteration versus the Objective values saved in the mdl.FitInfo property.

You can use the refit method with 'InitialFeatureWeights' equal to mdl.FeatureWeights to start from the current solution and run additional iterations

Example: 'InitialLearningRate',0.9

Data Types: double | single

Number of observations to use in each batch for the 'sgd' solver, specified as the comma-separated pair consisting of 'MiniBatchSize' and a positive integer from 1 to n.

Example: 'MiniBatchSize',25

Data Types: double | single

Maximum number of passes through all n observations for solver 'sgd', specified as the comma-separated pair consisting of 'PassLimit' and a positive integer. Each pass through all of the data is called an epoch.

Example: 'PassLimit',10

Data Types: double | single

Frequency of batches for displaying convergence summary for the 'sgd' solver , specified as the comma-separated pair consisting of 'NumPrint' and a positive integer. This argument applies when the 'Verbose' value is greater than 0. NumPrint mini-batches are processed for each line of the convergence summary that is displayed on the command line.

Example: 'NumPrint',5

Data Types: double | single

Number of tuning iterations for the 'sgd' solver, specified as the comma-separated pair consisting of 'NumTuningIterations' and a positive integer. This option is valid only for 'InitialLearningRate','auto'.

Example: 'NumTuningIterations',15

Data Types: double | single

Number of observations to use for tuning the initial learning rate, specified as the comma-separated pair consisting of 'TuningSubsetSize' and a positive integer value from 1 to n. This option is valid only for 'InitialLearningRate','auto'.

Example: 'TuningSubsetSize',25

Data Types: double | single

SGD or LBFGS Options

collapse all

Maximum number of iterations, specified as the comma-separated pair consisting of 'IterationLimit' and a positive integer. The default is 10000 for SGD and 1000 for LBFGS and mini-batch LBFGS.

Each pass through a batch is an iteration. Each pass through all of the data is an epoch. If the data is divided into k mini-batches, then every epoch is equivalent to k iterations.

Example: 'IterationLimit',250

Data Types: double | single

Convergence tolerance on the step size, specified as the comma-separated pair consisting of 'StepTolerance' and a positive real scalar. The 'lbfgs' solver uses an absolute step tolerance, and the 'sgd' solver uses a relative step tolerance.

Example: 'StepTolerance',0.000005

Data Types: double | single

Mini-Batch LBFGS Options

collapse all

Maximum number of iterations per mini-batch LBFGS step, specified as the comma-separated pair consisting of 'MiniBatchLBFGSIterations' and a positive integer.

Example: 'MiniBatchLBFGSIterations',15

Data Types: double | single

Note

The mini-batch LBFGS algorithm is a combination of SGD and LBFGS methods. Therefore, all of the name-value pair arguments that apply to SGD and LBFGS solvers also apply to the mini-batch LBFGS algorithm.

Output Arguments

collapse all

Neighborhood component analysis model for classification, returned as a FeatureSelectionNCAClassification object.

Version History

Introduced in R2016b

See Also

| | | | |

Topics