assignClusters

Assign observations to existing clusters and dynamic clusters

Since R2025a

collapse all in page

    Syntax

    idx = assignClusters(Mdl,X)
    [idx,D] = assignClusters(Mdl,X)
    [idx,D,idxDynamic] = assignClusters(Mdl,X)
    [idx,D,idxDynamic,DDynamic] = assignClusters(Mdl,X)

    Description

    idx = assignClusters(Mdl,X) returns cluster indices for the observations in X, using the incrementalDynamicKMeans model Mdl. You cannot call assignClusters if Mdl.NumPredictors is 0 or if all the values of Mdl.Centroids (or Mdl.DynamicCentroids) are NaN. When you call assignClusters, the software does not update Mdl.

    example

    [idx,D] = assignClusters(Mdl,X) additionally returns the cluster distances. Each row in D contains the distance of the corresponding observation in X from each cluster centroid, according to the distance metric in Mdl.Distance.

    [idx,D,idxDynamic] = assignClusters(Mdl,X) additionally returns the dynamic cluster indices. You can only use this syntax when Mdl.MergeClusters is true.

    [idx,D,idxDynamic,DDynamic] = assignClusters(Mdl,X) additionally returns the dynamic cluster distances. You can only use this syntax when Mdl.MergeClusters is true.

    example

    Examples

    collapse all

    Open Live Script

    Create a training data set of 10,000 observations of three predictors. The data set contains ten groups of 1000 observations each. The predictor values of each group centroid lie within the range ([–10,10], [–10,10], [–10,10]). Store the group identification numbers in ids.

    rng(0,"twister"); % For reproducibility
ngroups = 10;
obspergroup = 1000;
Xtrain = [];
ids = [];
cposrange = 10;
for c = 1:ngroups
    sigma = rand;
    Xtrain = [Xtrain; randn(obspergroup,3)*sigma + ...
        (randi(2*cposrange,[1,3])-cposrange).*ones(obspergroup,3)];
    ids = [ids; c*ones(obspergroup,1)];
end

    Shuffle the data set.

    ntrain = size(Xtrain,1);
indices = randperm(ntrain);
Xtrain = Xtrain(indices,:);
ids = ids(indices,:);

    Split off the last 2000 observations to create a test set.

    Xtest = Xtrain(end-1999:end,:);
idsTest = ids(end-1999:end,:);
Xtrain = Xtrain(1:end-2000,:);
ids = ids(1:end-2000,:);

    Plot the data set and color the observations according to their group number.

    scatter3(Xtrain(:,1),Xtrain(:,2),Xtrain(:,3),1,ids,"filled");
colormap(jet);

    Figure contains an axes object. The axes object contains an object of type scatter.

    Create Incremental Model

    Create an incremental dynamic k-means model object with numClusters=2 and default parameters.

    Mdl = incrementalDynamicKMeans(numClusters=2);

    Display the initial number of clusters and dynamic clusters.

    Mdl.NumClusters
    ans = 
11

    Mdl.NumDynamicClusters
    ans = 
11

    The software sets Mdl.NumClusters using the specified value of NumClusters and the default value of NumAdditionalClusters (10). Because the default value of MergeClusters is false, the cluster and dynamic cluster property values of Mdl are identical.

    Fit Incremental Clustering Model

    Fit the incremental dynamic clustering model to the data using the fit function. To simulate a data stream, fit the model in chunks of 50 observations at a time. Because default value of WarmupPeriod is 1000, updateMetrics only updates performance metrics after the 20th iteration. At each iteration:

    • Process 50 observations.

    • Store the number of clusters in numClusters to see how it evolves during incremental learning.

    • Overwrite the previous incremental model with a new one fitted to the incoming observations.

    • Update the window and cumulative simplified silhouette performance metrics using the updateMetrics function.

    • Store the metrics for the merged clusters in sil to see how they evolve during incremental learning.

    numObsPerChunk = 50;
n = size(Xtrain,1);
nchunk = floor(n/numObsPerChunk);
sil = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
numClusters = zeros(nchunk);
for j = 1:nchunk
    numClusters(j) = Mdl.NumClusters;
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    chunkrows = ibegin:iend;
    Mdl = fit(Mdl,Xtrain(chunkrows,:));
    Mdl = updateMetrics(Mdl,Xtrain(chunkrows,:));
    sil{j,:} = Mdl.Metrics{'SimplifiedSilhouette',:};
end

    Analyze Incremental Model During Training

    Plot the number of clusters at the start of each iteration.

    plot(numClusters)
xlabel("Iteration")
ylabel("Number of Clusters")

    Figure contains an axes object. The axes object with xlabel Iteration, ylabel Number of Clusters contains 160 objects of type line.

    The model initially has 11 clusters, and has 14 clusters at the final iteration.

    figure;
plot(sil.Variables);
xlim([0 nchunk])
ylabel("Simplified Silhouette")
xline(Mdl.WarmupPeriod/numObsPerChunk,"g-.")
legend(sil.Properties.VariableNames,Location="southeast")
xlabel("Iteration")

    Figure contains an axes object. The axes object with xlabel Iteration, ylabel Simplified Silhouette contains 3 objects of type line, constantline. These objects represent Cumulative, Window.

    The plot indicates that when the model becomes warm, the window performance metric value is 0.83. After the 90th iteration, the metric value steadily increases.

    Create a bar chart of the cluster counts after the final iteration.

    bar(Mdl.ClusterCounts)
xlabel("Cluster")

    Figure contains an axes object. The axes object with xlabel Cluster contains an object of type bar.

    The plot shows that the observations are distributed relatively equally among all clusters except clusters 2, 5, 6, 7, and 13.

    Plot the test data set and color the points according to the cluster assignments of the final trained model. Plot the fitted cluster centroids using blue pentagram markers.

    idx = assignClusters(Mdl,Xtest);
scatter3(Xtest(:,1),Xtest(:,2),Xtest(:,3),5,idx,"filled");
colormap(jet)
hold on
C = Mdl.Centroids;
scatter3(C(:,1),C(:,2),C(:,3),100,"b","Pentagram","filled");
hold off

    Figure contains an axes object. The axes object contains 2 objects of type scatter.

    The plot shows that some groups in the test set are fit by a single cluster, while others are fit by two clusters.

    Open Live Script

    Create a data set with 20,000 observations of three predictors. The data set contains two groups of 10,000 observations each. Store the group identification numbers in ids.

    rng(0,"twister"); % For reproducibility
ngroups = 2;
obspergroup = 10000;
Xtrain = [];
ids = [];
sigma = 0.4;
for c = 1:ngroups
    Xtrain = [Xtrain; randn(obspergroup,3)*sigma + ...
        (randi(2,[1,3])-1).*ones(obspergroup,3)];
    ids = [ids; c*ones(obspergroup,1)];
end

    Shuffle the data set.

    ntrain = size(Xtrain,1);
indices = randperm(ntrain);
Xtrain = Xtrain(indices,:);
ids = ids(indices,:);

    Create a test set that contains the last 2000 observations of the data set. Store the group identification numbers for the test set in idsTest. Keep the first 18,000 observations as the training set.

    Xtest = Xtrain(end-1999:end,:);
idsTest = ids(end-1999:end,:);
Xtrain = Xtrain(1:end-2000,:);
ids = ids(1:end-2000,:);

    Plot the training set, and color the observations according to their group identification number.

    scatter3(Xtrain(:,1),Xtrain(:,2),Xtrain(:,3),1,ids,"filled");

    Figure contains an axes object. The axes object contains an object of type scatter.

    Create Incremental Model

    Create an incremental dynamic k-means model object with a warm-up period of 1000 observations. Specify that the incremental fit function stores two clusters that are merged from the dynamic clusters. 

    Mdl = incrementalDynamicKMeans(numClusters=2, ...
    WarmupPeriod=1000, MergeClusters=true)
    Mdl = 
  incrementalDynamicKMeans

                IsWarm: 0
               Metrics: [1×2 table]
           NumClusters: 2
    NumDynamicClusters: 11
             Centroids: [2×0 double]
      DynamicCentroids: [11×0 double]
              Distance: "sqeuclidean"


  Properties, Methods

    Mdl is an incrementalDynamicKMeans model object that is prepared for incremental learning.

    Fit Incremental Clustering Model

    Fit the incremental clustering model Mdl to the data using the fit function. To simulate a data stream, fit the model in chunks of 100 observations at a time. Because WarmupPeriod = 1000, fit only returns cluster indices after the tenth iteration. At each iteration:

    • Process 100 observations.

    • Store the number of dynamic clusters in numDynClusters, to see how it evolves during incremental learning.

    • Overwrite the previous incremental model with a new one fitted to the incoming observations.

    • Update the simplified silhouette performance metrics (Cumulative and Window) using the updateMetrics function.

    • Store the metrics for the merged clusters in sil and the metrics for the dynamic clusters in dynsil, to see how they evolve during incremental learning.

    numObsPerChunk = 100;
n = size(Xtrain,1);
nchunk = floor(n/numObsPerChunk);
sil = array2table(zeros(nchunk,2),"VariableNames",["Cumulative" "Window"]);
dynsil = array2table(zeros(nchunk,2),"VariableNames",["Cumulative" "Window"]);
numDynClusters = [];
for j = 1:nchunk
    numDynClusters(j) = Mdl.NumDynamicClusters;
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    chunkrows = ibegin:iend;
    Mdl = fit(Mdl,Xtrain(chunkrows,:));
    Mdl = updateMetrics(Mdl,Xtrain(chunkrows,:));
    sil{j,:} = Mdl.Metrics{"SimplifiedSilhouette",:};
    dynsil{j,:} = Mdl.DynamicMetrics{"SimplifiedSilhouette",:};
end

    Analyze Incremental Model During Training

    Plot the number of dynamic clusters at the start of each iteration.

    plot(numDynClusters)
xlabel("Iteration");

    Figure contains an axes object. The axes object with xlabel Iteration contains an object of type line.

    The model initially has 11 dynamic clusters, and 14 dynamic clusters at the final iteration.

    Plot the mean simplified silhouette metric for the merged clusters and the dynamic clusters. 

    figure;
t = tiledlayout(2,1);
nexttile
h = plot(sil.Variables);
ylabel("Simplified Silhouette")
xline(Mdl.WarmupPeriod/numObsPerChunk,"b:")
legend(h,sil.Properties.VariableNames,Location="southeast")
title("Merged Cluster Metrics")
nexttile
h2 = plot(dynsil.Variables);
ylabel("Simplified Silhouette")
xline(Mdl.WarmupPeriod/numObsPerChunk,"b:")
legend(h2,dynsil.Properties.VariableNames,Location="northeast")
xlabel(t,"Iteration")
title("Dynamic Cluster Metrics")

    Figure contains 2 axes objects. Axes object 1 with title Merged Cluster Metrics, ylabel Simplified Silhouette contains 3 objects of type line, constantline. These objects represent Cumulative, Window. Axes object 2 with title Dynamic Cluster Metrics, ylabel Simplified Silhouette contains 3 objects of type line, constantline. These objects represent Cumulative, Window.

    After the warm-up period, the updateMetrics function returns performance metrics. A high metric value indicates that, on average, each observation is well matched to its own cluster and poorly matched to other clusters. The higher metric values in the top plot indicate that the merged clusters provide a better clustering solution for the data than the unmerged dynamic clusters.

    Analyze the Final Clustering Model Using the Test Set

    Create a bar chart of the dynamic cluster counts after the final iteration.

    figure
bar(Mdl.DynamicClusterCounts)
xlabel("Dynamic Cluster Number");

    Figure contains an axes object. The axes object with xlabel Dynamic Cluster Number contains an object of type bar.

    The bar chart shows that the model assigns the observations equally among the dynamic clusters.

    Plot the test data set, and color the points according to the dynamic cluster assignments of the final trained model. Plot the dynamic cluster centroids using blue pentagram markers.

    C = Mdl.DynamicCentroids;
[~,~,dynIdx] = assignClusters(Mdl,Xtest);
figure;
scatter3(Xtest(:,1),Xtest(:,2),Xtest(:,3),3,dynIdx,"filled");
hold on
scatter3(C(:,1),C(:,2),C(:,3),100,"b","Pentagram","filled");
hold off

    Figure contains an axes object. The axes object contains 2 objects of type scatter.

    The dynamic cluster centroids are located within the overall distribution of the observations, and are equally divided among the two groups in the data.

    Plot the test data set and color the points according to the merged cluster assignments of the final trained model. Use the color red for the observations whose merged cluster assignments do not match the group identification numbers. Plot the merged cluster centroids using blue pentagram markers.

    C = Mdl.Centroids;
idx = assignClusters(Mdl,Xtest);
incorrectIds = find(idx ~= idsTest);
figure;
scatter3(Xtest(:,1),Xtest(:,2),Xtest(:,3),1,idx,"filled");
hold on
scatter3(C(:,1),C(:,2),C(:,3),100,"b","Pentagram","filled");
scatter3(Xtest(incorrectIds,1),Xtest(incorrectIds,2),Xtest(incorrectIds,3),5,"r","filled")
hold off

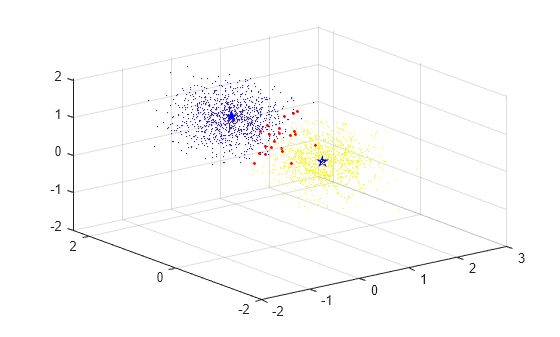
    Figure contains an axes object. The axes object contains 3 objects of type scatter.

    The plot shows that the merged centroids lie near the center of each group in the data. The observations with incorrect cluster assignments lie mainly in the region in between the two groups.

    Use the helper function AdjustedRandIndex to calculate the adjusted Rand index, which measures the similarity of the clustering indices and the group identification numbers.

    AdjustedRandIndex(idx,idsTest)
    ans = 
0.9584

    The adjusted Rand index is close to 1, indicating that the clustering model does a good job of correctly predicting the group identification numbers of the test set observations.

    function ARI = AdjustedRandIndex(labels1, labels2)
% Helper function to calculate the Adjusted Rand Index (ARI) to
% measure the similarity between two clustering labels labels1
% and labels2.

C = confusionmat(labels1, labels2);
n = numel(labels2);

% Calculate sums for rows and columns
sumRows = sum(C, 2);
sumCols = sum(C, 1);

ss = sum(C.^2,"all");

TN = ss-n;                 % True negatives
FP = sum(C*sumCols')-ss;   % False positives
FN = sum(C'*sumRows)-ss;   % False negatives
TP = n^2-FP-FN-ss;         % True positives

if FN == 0 && FP == 0
    ARI = 1;
else
    ARI = 2*(TP*TN-FN*FP)/((TP+FN)*(FN+TN)+(TP+FP)*(FP+TN));
end

end

% LocalWords:  ARI

    Input Arguments

    collapse all

    Incremental dynamic k-means clustering model, specified as an incrementalDynamicKMeans model object. You can create Mdl by calling incrementalDynamicKMeans directly.

    Chunk of predictor data, specified as a numeric matrix of n observations and Mdl.NumPredictors variables. The rows of X correspond to observations, and the columns correspond to variables. If a row of X contains a missing value, the corresponding values of idx and D for that row are NaN.

    Note

    assignClusters supports only numeric input predictor data. If your input data includes categorical data, you must prepare an encoded version of the categorical data. Use dummyvar to convert each categorical variable to a numeric matrix of dummy variables. Then, concatenate all dummy variable matrices and any other numeric predictors. For more details, see Dummy Variables.

    Data Types: single | double

    Output Arguments

    collapse all

    Cluster indices, returned as a size(X,1)-by-1 vector of integers. assignClusters uses Mdl.Centroids to assign the cluster indices. If a row of X contains a missing value, the corresponding value of idx is NaN. assignClusters does not return indices of clusters whose corresponding Centroids values are NaN.

    Cluster distances, returned as a size(X,1)-by-Mdl.NumClusters numeric matrix. assignClusters uses Mdl.Centroids to determine the cluster distances. Each row in D contains the distance of the corresponding observation in X from each cluster centroid in Mdl.Centroids, according to the distance metric in Mdl.Distance. If a cluster has no observations assigned to it, or its corresponding Mdl.Centroids values are NaN, the distance value for all observations to that cluster is NaN. If a row of X contains a missing value, the corresponding row of D contains all NaN values.

    Dynamic cluster indices, returned as a size(X,1)-by-1 vector of integers. assignClusters uses Mdl.DynamicCentroids to assign the dynamic cluster indices. If a row of X contains a missing value, the corresponding value of idxDynamic is NaN. assignClusters does not return cluster indices of clusters whose corresponding DynamicCentroids values are NaN.

    Dynamic cluster distances, returned as a size(X,1)-by-Mdl.NumDynamicClusters numeric matrix. assignClusters uses Mdl.DynamicCentroids to determine the dynamic cluster distances. Each row in D contains the distance of the corresponding observation in X from each cluster centroid in Mdl.DynamicCentroids, according to the distance metric in Mdl.Distance. If a dynamic cluster has no observations assigned to it, or its corresponding Mdl.DynamicCentroids values are NaN, the distance value for all observations to that cluster is NaN. If a row of X contains a missing value, the corresponding row of DDynamic contains all NaN values.

    Version History

    Introduced in R2025a

    See Also

    Functions