fit

Fit model for incremental k-means clustering

Since R2025a

collapse all in page

    Syntax

    Mdl = fit(Mdl,X)
    [Mdl,idx] = fit(Mdl,X)

    Description

    The fit function fits a configured model for incremental k-means clustering (incrementalKMeans object) to streaming data.

    To fit a k-means clustering model to an entire batch of data at once, use kmeans.

    Mdl = fit(Mdl,X) returns a k-means clustering model Mdl, which is the input incrementalKMeans model object Mdl fit using the predictor data X. Specifically, the incremental fit function fits the model to the incoming data and stores the updated clustering properties in the output model Mdl. For more information, see Incremental k-Means Clustering.

    example

    [Mdl,idx] = fit(Mdl,X) additionally returns the cluster indices idx for the observations in X.

    example

    Examples

    collapse all

    Open Live Script

    Create an incremental model for k-means clustering that has two clusters.

    Mdl = incrementalKMeans(numClusters=2)
    Mdl = 
  incrementalKMeans

         IsWarm: 0
        Metrics: [1×2 table]
    NumClusters: 2
      Centroids: [2×0 double]
       Distance: "sqeuclidean"


  Properties, Methods

    Mdl is an incrementalKMeans model object. All its properties are read-only.

    Load and Preprocess Data

    Load the New York city housing data set.

    load NYCHousing2015.mat

    The data set includes 10 variables with information on the sales of properties in New York City in 2015. Keep only the gross square footage and sale price predictors. Keep all records that have a gross square footage above 100 square feet and a sales price above $1000. 

    data = NYCHousing2015(:,{'GROSSSQUAREFEET','SALEPRICE'});
data = data((data.GROSSSQUAREFEET > 100 & data.SALEPRICE > 1000),:);

    Convert the tabular data into a matrix that contains the logarithm of both predictors.

     X = table2array(log10(data));

    Randomly shuffle the order of the records.

     rng(0,"twister"); % For reproducibility
 X = X(randperm(size(X,1)),:);

    Fit and Plot Incremental Model

    Fit the incremental model Mdl to the data by using the fit function. To simulate a data stream, fit the model in chunks of 500 records at a time. At each iteration:

    • Process 500 observations.

    • Overwrite the previous incremental model with a new one fitted to the incoming records.

    • Update the performance metrics for the model. The default metric for Mdl is SimplifiedSilhouette.

    • Store the cumulative and window metrics to see how they evolve during incremental learning.

    • Compute the cluster assignments of all records seen so far, according to the current model.

    • Plot all records seen so far, and color each record by its cluster assignment.

    • Plot the current centroid location of each cluster.

    In this workflow, the updateMetrics function provides information about the model's clustering performance after it is fit to the incoming data chunk. In other workflows, you might want to evaluate a clustering model's performance on unseen data. In such cases, you can call updateMetrics prior to calling the incremental fit function. 

    % Initialize plot properties
hold on
h1 = scatter(NaN,NaN,0.3);
h2 = plot(NaN,NaN,Marker="o", ...
    MarkerFaceColor="k",MarkerEdgeColor="k");
h3 = plot(NaN,NaN,Marker="^", ...
    MarkerFaceColor="b",MarkerEdgeColor="b");
colormap(gca,"prism")
pbaspect([1,1,1])
xlim([min(X(:,1)),max(X(:,1))]);
ylim([min(X(:,2)),max(X(:,2))]);
xlabel("log Gross Square Footage");
ylabel("log Sales Price in Dollars")

% Incremental fitting and plotting
n = numel(X(:,1));
numObsPerChunk = 500;
nchunk = floor(n/numObsPerChunk);
sil = array2table(zeros(nchunk,2),VariableNames=["Cumulative" "Window"]);

for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = fit(Mdl,X(idx,:));
    Mdl = updateMetrics(Mdl,X(idx,:));
    sil{j,:} = Mdl.Metrics{'SimplifiedSilhouette',:};
    indices = assignClusters(Mdl,X(1:iend,:));
    title("Iteration " + num2str(j))
    set(h1,XData=X(1:iend,1),YData=X(1:iend,2),CData=indices);
    set(h2,Marker="none") % Erase previous centroid markers
    set(h3,Marker="none")
    set(h2,XData=Mdl.Centroids(1,1),YData=Mdl.Centroids(1,2),Marker="o")
    set(h3,Xdata=Mdl.Centroids(2,1),YData=Mdl.Centroids(2,2),Marker="^")
    pause(0.5);
end
    Warning: Hardware-accelerated graphics is unavailable. Displaying fewer markers to preserve interactivity.

    hold off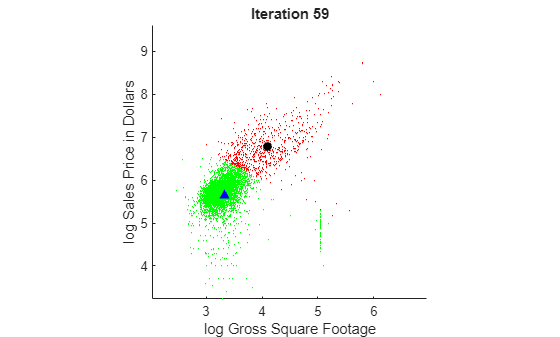

    Figure contains an axes object. The axes object with title Iteration 59, xlabel log Gross Square Footage, ylabel log Sales Price in Dollars contains 3 objects of type scatter, line.

    To view the animated figure, you can run the example, or open the animated gif below in your web browser.

    FixedNumberofClusters.gif

    At each iteration, the animated plot displays all the observations processed so far as small circles, and colors them according to the cluster assignments of the current model. The black circle indicates the centroid position of cluster 1, and the blue triangle indicates the centroid position of cluster 2.

    Plot the window and cumulative metrics values at each iteration.

    h4 = plot(sil.Variables);
xlabel("Iteration")
ylabel("Performance Metric")
xline(Mdl.WarmupPeriod/numObsPerChunk,'g-.')
legend(h4,sil.Properties.VariableNames,Location="southeast")

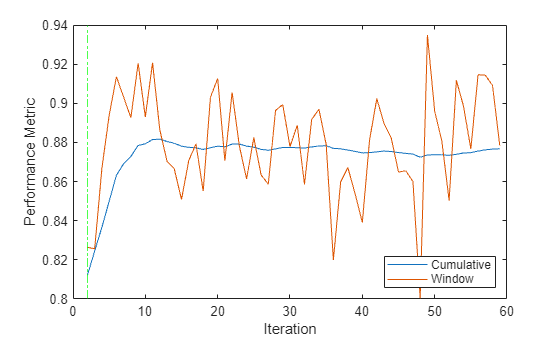
    Figure contains an axes object. The axes object with xlabel Iteration, ylabel Performance Metric contains 3 objects of type line, constantline. These objects represent Cumulative, Window.

    The updateMetrics function calculates the performance metrics after the end of the warm-up period. The performance metrics rise rapidly from an initial value of 0.81 and approach a value of approximately 0.88 after 10 iterations.

    Open Live Script

    Create a set of noisy position measurements of two moving objects. Object 1 starts at (x,y) coordinate (-50,0) and moves along the x-axis. Object 2 starts at (x,y) coordinate (0,-40) and moves along the y-axis. The objects move at the same speed.

    Generate numObsPerStep=100 measurements of each object at numSteps=100 individual time steps. 

    rng(0,"twister") % For reproducibility
sigma = 2;  % Measurement noise level
numObsPerStep = 100;
numSteps = 100;
startPosA = [-50,0];
startPosB = [0,-40];
X = [];
for t = 0:numSteps-1
    for i = 1:numObsPerStep
        p = randn(1,4)*sigma;  % Gaussian measurement noise
        X = [X;[[p(1)+t+startPosA(1);p(2)+startPosB(1)], ...
            [p(3)+startPosA(2);p(4)+t+startPosB(2)]]];
    end
end

    The rows of X contain 2*numObsPerStep*numSteps position measurements. The columns of X contain the x and y coordinates of each measurement, respectively.

    Create Incremental k-Means Clustering Models

    To track the centroids of the moving clusters, create two incremental k-means clustering model objects that each have two clusters and no warm-up period. Specify a forgetting factor value of 0.1 for the first model, and 0.75 for the second model. A lower value of the forgetting factor (which can range from 0 to 1) assigns more weight to older measurements when the incremental fit algorithm calculates new cluster centroids.

    MdlA = incrementalKMeans(numClusters=2,WarmupPeriod=0, ...
    ForgettingFactor=0.1);
MdlB = incrementalKMeans(numClusters=2,WarmupPeriod=0, ...
    ForgettingFactor=0.75);

    Fit and Plot Incremental Models

    Fit the incremental k-means clustering models to the data by using the fit function. Fit the models in data chunks that consist of the measurements at each time step. At each iteration:

    • Process 2*numObsPerStep observations.

    • Overwrite the previous incremental models with new ones fitted to the incoming measurements.

    • Update the performance metrics for the models. The metric for the models is SimplifiedSilhouette.

    • Store the cumulative and window metrics to see how they evolve during incremental learning.

    • Compute the cluster assignments of the incoming chunk of measurements, according to the current model A.

    • Plot the incoming chunk of measurements, and color each measurement by its cluster assignment according to model A.

    • Plot the current model centroid locations for each cluster.

    • Plot all of the previous measurements using gray points.

    % Initialize plot properties
hold on
h1 = scatter(NaN,NaN,0.2,[0.9 0.9 0.9],".");
h2 = scatter(NaN,NaN,1.5); 
h3 = plot(NaN,NaN,"^",MarkerSize=6,MarkerEdgeColor="k", ...
    MarkerFaceColor="k"); 
h4 = plot(NaN,NaN,"square",MarkerSize=6,MarkerEdgeColor="b", ...
    MarkerFaceColor="b");
colormap(gca,"prism")
xlim([min(X(:,1)),max(X(:,1))]);
ylim([min(X(:,2)),max(X(:,2))]);
xlabel("X");
ylabel("Y");
% Incremental fitting and plotting
n = numel(X(:,1));
nChunk = 2*numObsPerStep;
silA = array2table(zeros(numSteps,2), ...
    'VariableNames',["Cumulative" "Window"]);
silB = array2table(zeros(numSteps,2), ...
    'VariableNames',["Cumulative" "Window"]);
for j = 1:numSteps
    ibegin = min(n,nChunk*(j-1) + 1);
    iend = min(n,nChunk*j);
    idx = ibegin:iend;    
    [MdlA,indices] = fit(MdlA,X(idx,:));
    MdlA = updateMetrics(MdlA,X(idx,:));
    MdlB = fit(MdlB,X(idx,:));
    MdlB = updateMetrics(MdlB,X(idx,:));
    title("Iteration " + num2str(j))
    silA{j,:} = MdlA.Metrics{'SimplifiedSilhouette',:};
    silB{j,:} = MdlB.Metrics{'SimplifiedSilhouette',:};
    set(h1,XData=X(1:ibegin-1,1),YData=X(1:ibegin-1,2));
    set(h2,XData=X(idx,1),YData=X(idx,2),CData=indices);
    set(h3,Marker="none") % Erase the previous centroid markers
    set(h4,Marker="none")
    set(h3,XData=MdlA.Centroids(:,1),YData=MdlA.Centroids(:,2), ...
        Marker="^");
    set(h4,XData=MdlB.Centroids(:,1),YData=MdlB.Centroids(:,2), ...
        Marker="square");
    pause(0.2);
end
hold off

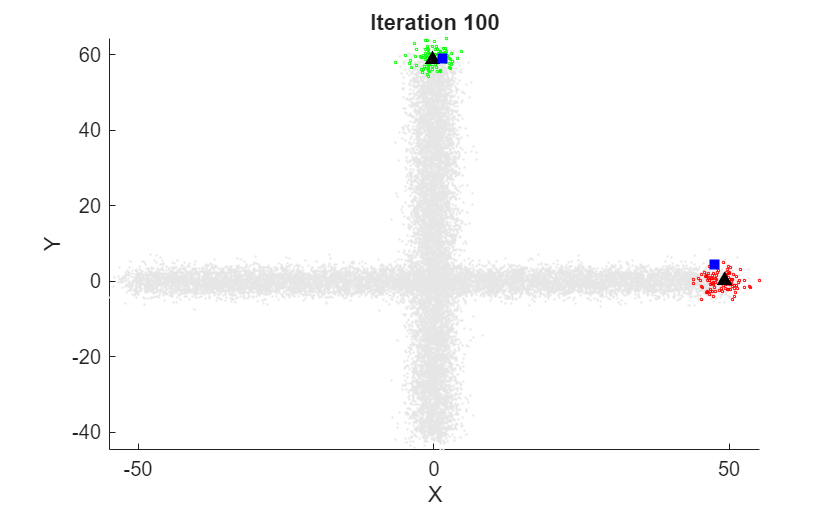
    Figure contains an axes object. The axes object with title Iteration 100, xlabel X, ylabel Y contains 4 objects of type scatter, line. One or more of the lines displays its values using only markers

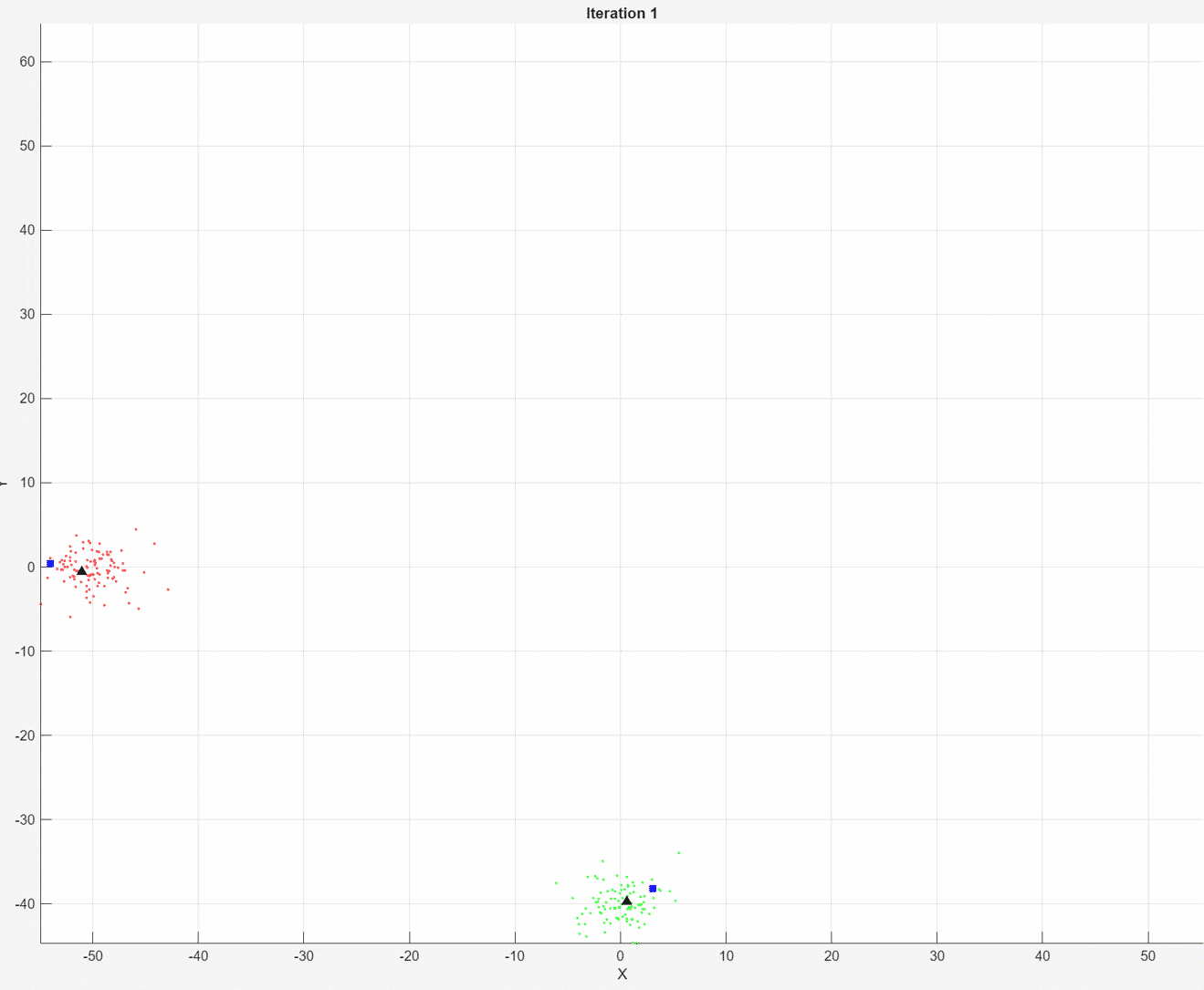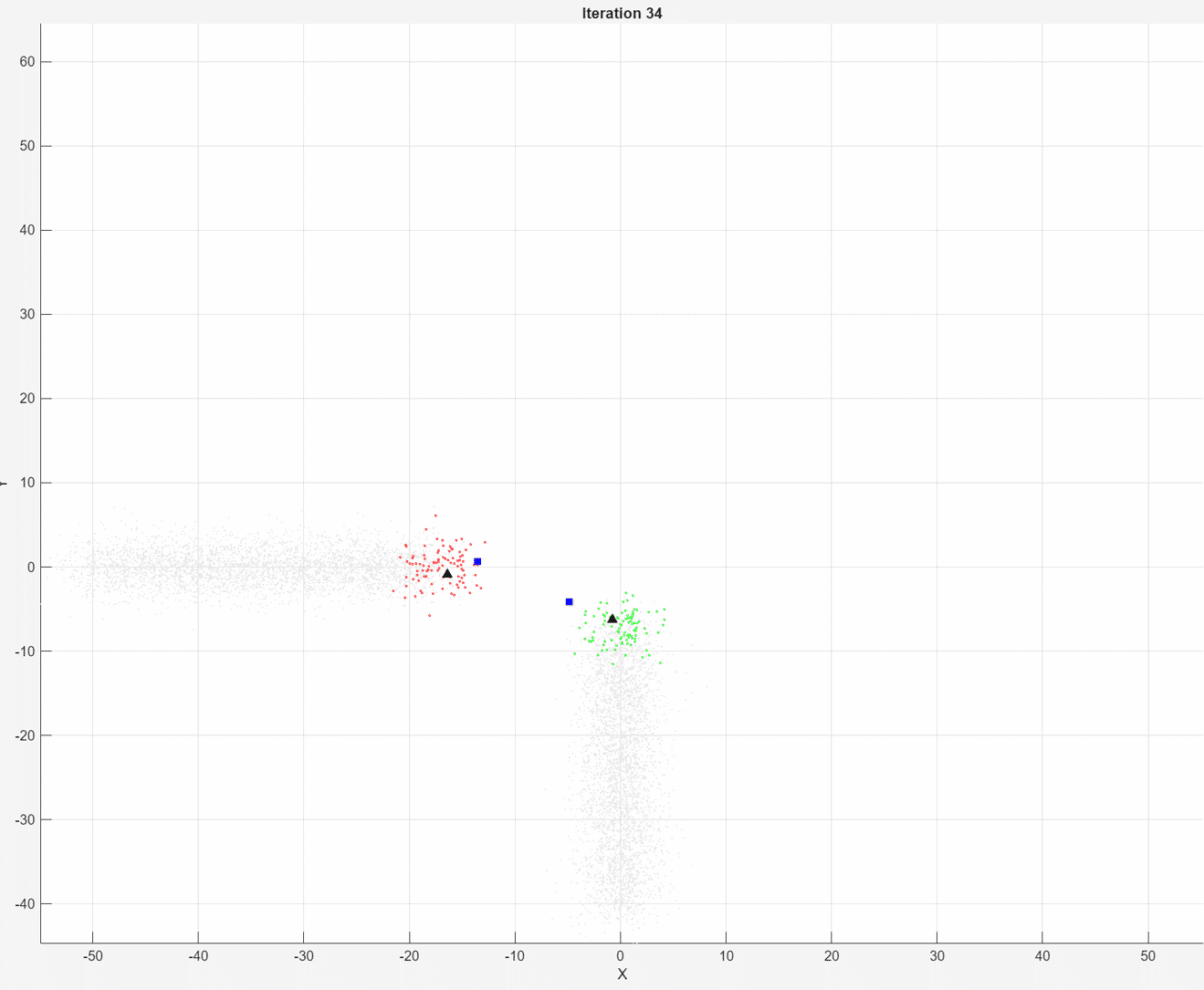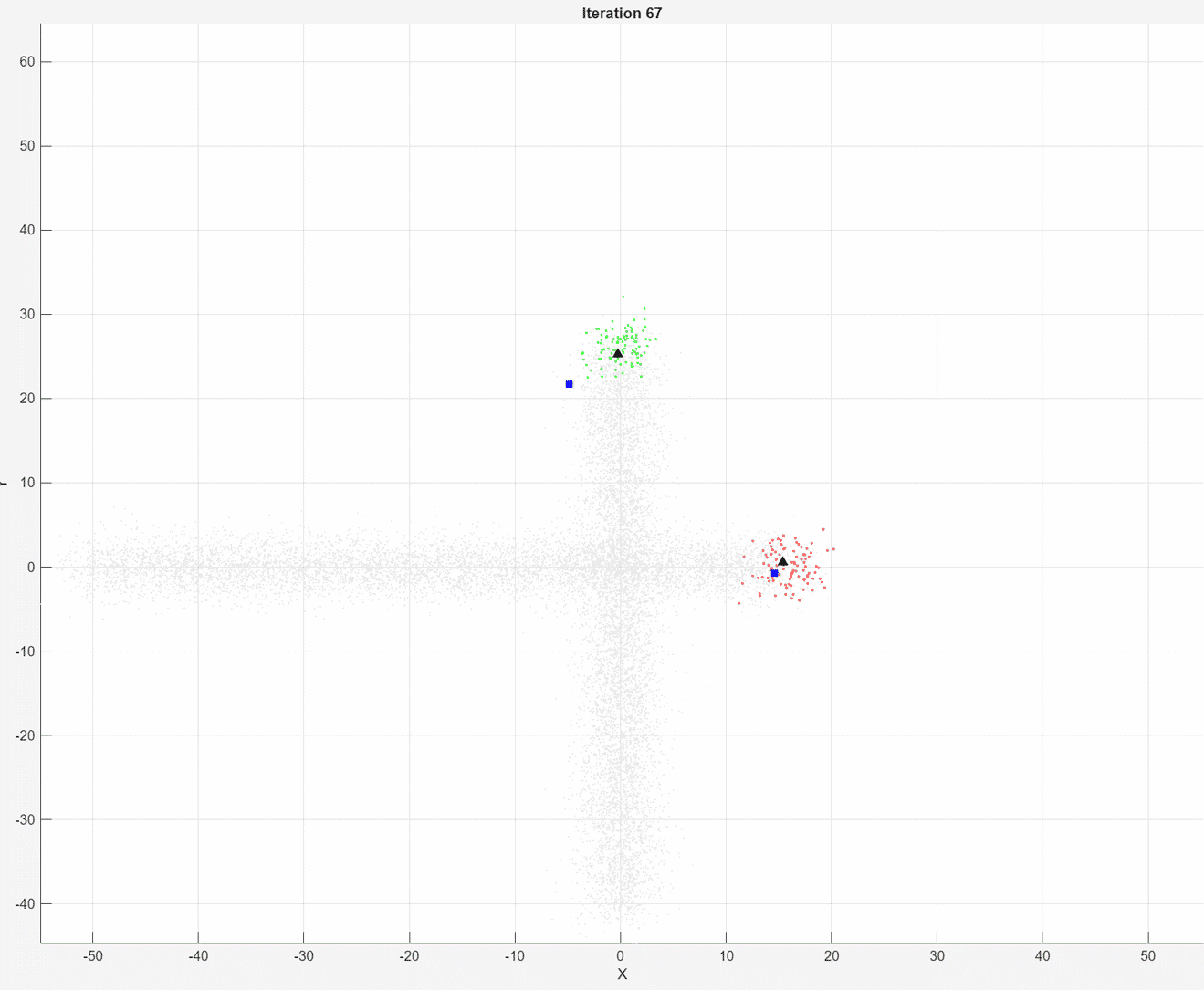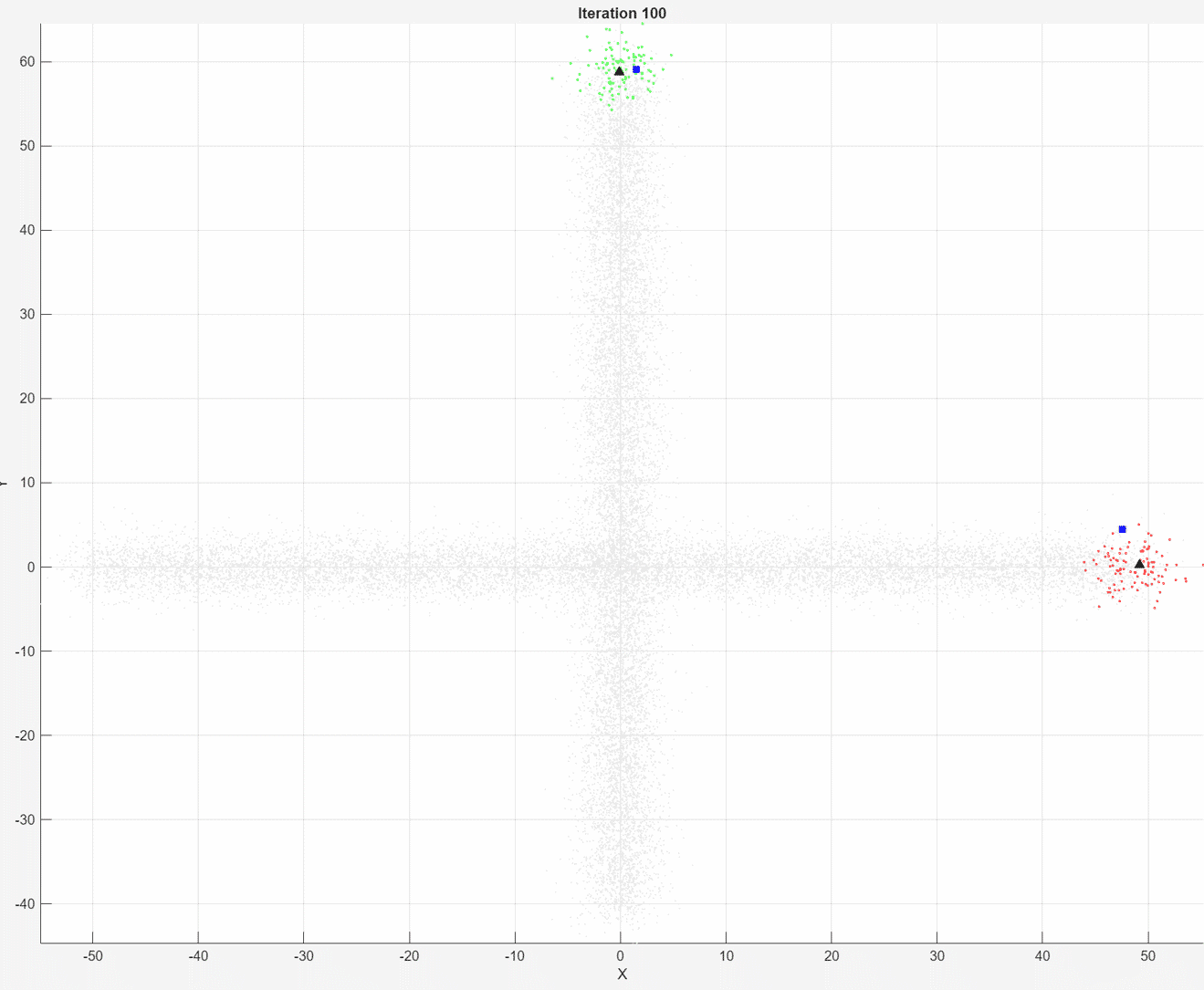    FitMovingCentroids.gifAt each iteration, the animated plot displays all of the position measurements processed so far in gray. The incremental fit function tracks the centroid of each object at each iteration. The measurements in the current data chunk are colored according to the cluster assignment of model A. The black upward-pointing triangles and blue squares indicate the fitted cluster centroids of models A and B, respectively.

    Model A does a good job of tracking the true position of each moving object. Because model B has a higher forgetting factor, the fit function assigns the highest weights to the most recent measurements. Therefore, model B does a poorer job of tracking the true positions of the objects.

    Plot the simplified silhouette performance metrics at each iteration.

    h5 = plot([silA.Variables,silB.Variables]);
xlabel("Iteration")
ylabel("Simplified Silhouette")
legend(h5,{"Cumulative A","Window A", ...
    "Cumulative B","Window B"},Location="southwest")

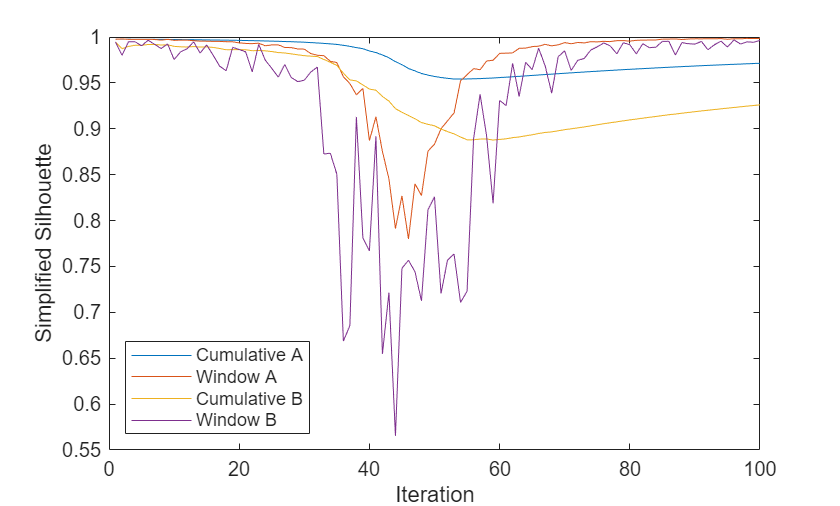
    Figure contains an axes object. The axes object with xlabel Iteration, ylabel Simplified Silhouette contains 4 objects of type line. These objects represent Cumulative A, Window A, Cumulative B, Window B.

    The plot shows that the simplified silhouette values of model B are poorer than those of model A. The values of both models dip significantly between iterations 30 and 60, when the two objects are close to each other. As the objects move apart, the window values of both models return to their previous levels.

    Input Arguments

    collapse all

    Incremental k-means clustering model, specified as an incrementalKMeans model object. You can create Mdl by calling incrementalKMeans directly.

    Chunk of predictor data, specified as an n-by-Mdl.NumPredictors numeric matrix. The rows of X correspond to observations, and the columns correspond to predictor variables. The software ignores observations that contain at least one missing value.

    Note

    • If Mdl.NumPredictors=0, fit infers the number of predictors from X, and sets the corresponding property of the output model. Otherwise, if the number of predictor variables (columns) in X differs from Mdl.NumPredictors, then fit issues an error.

    • fit supports only numeric input predictor data. If your input data includes categorical data, you must prepare an encoded version of the categorical data. Use dummyvar to convert each categorical variable to a numeric matrix of dummy variables. Then, concatenate all dummy variable matrices and any other numeric predictors. For more details, see Dummy Variables.

    Data Types: single | double

    Output Arguments

    collapse all

    Updated incremental k-means clustering model, returned as an incrementalKMeans model object.

    Cluster indices, returned as a numeric column vector of length size(X,1). If Mdl is not warm (IsWarm=false) when the software processes an observation in X, the corresponding value of idx is NaN.

    More About

    collapse all

    References

    [1] Lloyd, S. Least Squares Quantization in PCM. IEEE Transactions on Information Theory 28, no. 2 (March 1982): 129–37.

    [2] Sculley, D. Web-Scale k-Means Clustering. In Proceedings of the 19th International Conference on World Wide Web, 1177–78. Raleigh North Carolina USA: ACM, 2010.

    Version History

    Introduced in R2025a

    See Also

    Functions