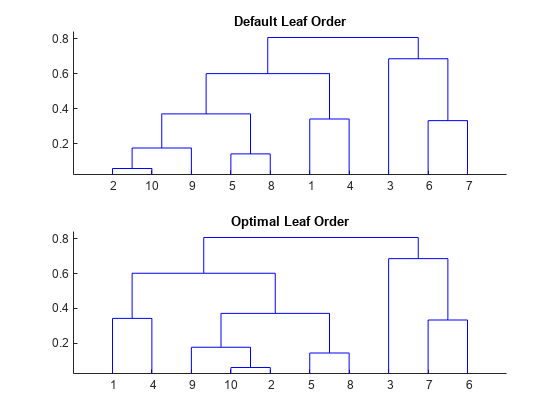
optimalleaforder
Optimal leaf ordering for hierarchical clustering
Description
leafOrder = optimalleaforder(tree,D)tree, using the distances, D. An optimal
leaf ordering of a binary tree maximizes the sum of the similarities between
adjacent leaves by flipping tree branches without dividing the clusters.
leafOrder = optimalleaforder(tree,D,Name,Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
References
[1] Bar-Joseph, Z., Gifford, D.K., and Jaakkola, T.S. (2001). "Fast optimal leaf ordering for hierarchical clustering." Bioinformatics Vol. 17, Suppl 1:S22–9. PMID: 11472989.
Version History
Introduced in R2012b
See Also
dendrogram | linkage | pdist