可视化多元数据
此示例说明如何使用统计图可视化多元数据。许多统计分析只涉及两个变量:预测变量和响应变量。使用二维散点图、二元直方图和箱线图等绘图可以轻松地可视化这两个变量。您还可以使用三维散点图或二维散点图可视化三元数据,其中第三个变量用颜色表示。但是,许多数据集涉及大量变量,使直接可视化变得更加困难。此示例探究如何使用 Statistics and Machine Learning Toolbox™ 中的函数来可视化高维数据。
加载数据
加载 carbig 数据集,其中包含 20 世纪 70 年代和 80 年代生产的约 400 辆汽车的测量值。使用多元可视化来探究燃油效率(每加仑汽油可行驶的英里数,以 MPG 为单位)、加速度(从 0 mph 到 60 mph 需要的时间,以秒为单位)、发动机排量(以立方英寸为单位)、重量和马力等值。
load carbig X = [MPG,Acceleration,Displacement,Weight,Horsepower]; varNames = ["MPG","Acceleration","Displacement","Weight","Horsepower"];
散点图矩阵
查看高维数据的一种方式是显示低维子空间中的数据切片。使用 gplotmatrix 函数显示 X 中五个变量的所有二元散点图的数组,以及表示每个变量自身的一元直方图。根据气缸数量对观测值进行分组。
gplotmatrix(X,[],Cylinders,[],[],8,[],[],varNames)

每个散点图中的点按气缸数量进行着色:红色表示 4 缸,紫色表示 6 缸,绿色表示 8 缸。装有转子发动机的汽车有 3 个气缸,少数汽车有 5 个气缸。这组图有助于您找出变量对之间的关系模式。更高维度中的重要模式可能存在,但它们在此图中不易识别。
平行坐标图
虽然散点图矩阵仅显示二元关系,但有些图会同时显示所有变量,并允许您研究变量之间的更高维关系。最简单的多元图就是平行坐标图。此图中的坐标轴是水平排列的,而不是像典型的笛卡尔图那样正交排列。每个观测项在图中表示为一条由几个线段连接起来的连接线。
创建一个涵盖 X 中所有 4 缸、6 缸或 8 缸汽车的绘图,并用颜色对观测值进行分组。
cyl468 = ismember(Cylinders,[4 6 8]); parallelcoords(X(cyl468,:),Group=Cylinders(cyl468), ... Standardize="on",Labels=varNames)

在此图中,水平方向表示坐标轴,垂直方向表示数据。每个观测项由五个变量的测量值组成,每个测量值由对应的线条在每个坐标轴上的高度表示。由于五个变量的范围相差很大,因此图中的每个变量都标准化为均值为 0、方差为 1。图中的着色显示,8 缸汽车通常具有较低的 MPG 和加速度值,以及较高的排量、重量和马力值。
在查看包含大量观测值的平行坐标图时,可能不够清晰直观。要缓解此问题,您可以创建一个平行坐标图,其中只显示每组的中位数以及上四分位数和下四分位数(25% 个点和 75% 个点)。此图有助于更好地区分各组,但不包括可能感兴趣的观测值,如组离群值。
parallelcoords(X(cyl468,:),Group=Cylinders(cyl468), ... Standardize="on",Labels=varNames,Quantile=0.25)

安德鲁斯图
另一种类型的多元可视化是安德鲁斯图。此图将每个观测值表示为区间 [0,1] 内的平滑函数。
andrewsplot(X(cyl468,:),Group=Cylinders(cyl468),Standardize="on")
每个函数均为一个傅里叶级数,系数等于对应的观测值。在此示例中,级数有五个项:一个常项、两个正弦项(周期为 1 和 1/2)和两个与之相似的余弦项。前三个项对每个函数形状的影响是最明显的。也就是说,前三个变量的模式往往最容易识别。
绘图显示在 t = 0 处各组之间的显著差异。此差异表明,第一个变量 MPG 是区分 4 缸、6 缸或 8 缸汽车的特征之一。大约在 t = 1/3 处各组之间的差异也很有趣。在安德鲁斯图函数的公式中输入此值。所得的结果是一组定义变量线性组合的系数。这种线性组合有助于将一个组与其他组区分开来。
t1 = 1/3; coeffs = [1/sqrt(2) sin(2*pi*t1) cos(2*pi*t1) sin(4*pi*t1) cos(4*pi*t1)]
coeffs = 1×5
0.7071 0.8660 -0.5000 -0.8660 -0.5000
这些系数表明,与 8 缸汽车相比,4 缸汽车具有较高的 MPG 和加速度值,以及较低的排量值、马力值,特别是重量值。此结论与从平行坐标图中得出的结论一致。
图形符号图
您还可以通过使用图形符号表示维度来可视化多元数据。函数 glyphplot 支持两种图形符号:星座图和切尔诺夫脸谱图。创建一个涵盖数据集中前九个车型的星座图。星座的每一条边代表一个变量,边长与代表该观测值的变量值成正比。
g = glyphplot(X(1:9,:),Glyph="star",VarLabels=varNames, ... ObsLabels=Model(1:9,:)); set(g(:,3),FontSize=8);
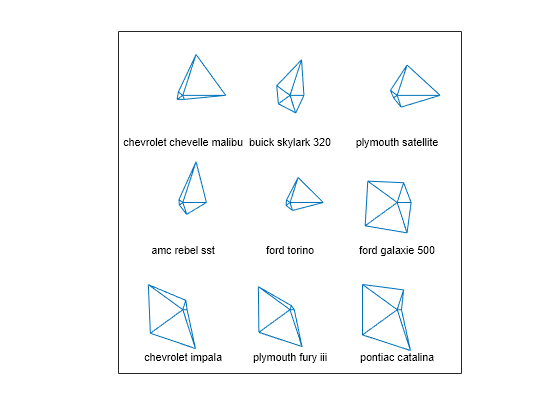
在图窗窗口中,此图允许您通过使用数据游标以交互方式探查数据值。例如,点击代表 Ford Torino 的星座中最右侧的点,将显示该汽车的 MPG 值为 17。
图形符号图和多维尺度分析
如果您在网格上无序绘制各星座,有时在创建的图窗中相邻的星座可能看起来完全不同。您可能无法直观地识别任何模式。为了有助于模式识别,可以将多维尺度分析 (MDS) 与图形符号图结合起来。
首先,选择 1977 年的所有汽车,然后使用 zscore 函数将五个变量都标准化,使其均值为 0、方差为 1。然后,计算标准化观测值中的欧几里德距离作为相异度的测度。对于更复杂的应用程序,可以考虑使用不太简单的相异度的测度。
models77 = find((Model_Year==77)); dissimilarity = pdist(zscore(X(models77,:)));
最后,使用 mdscale 创建一组二维位置(其点间距离近似于原始高维数据点之间的相异度)。使用以下位置绘制图形符号。生成的二维绘图中的距离粗略地重现数据。
Y = mdscale(dissimilarity,2); figure glyphplot(X(models77,:),Glyph="star",Centers=Y, ... VarLabels=varNames,ObsLabels=Model(models77,:),Radius=0.5) title("1977 Model Year")

二维绘图使用 MDS 作为降维方法。通常,降维意味着信息丢失,但图形符号包括数据中的所有高维信息。使用 MDS 是为了使数据的变化呈现某种规律性,从而更容易看到图形符号中的模式。
与前面的图一样,您可以使用图窗窗口以交互方式探索此图。
另一种图形符号是切尔诺夫脸谱图。此图形符号将每个观测值的数据值编码为面部特征,例如面孔的大小、面孔的形状、眼睛的位置等。绘图中何种关系最为明显取决于特征与变量的对应关系。使用 glyphplot 指定这种对应关系。
figure facePlot = glyphplot(X(models77,:),Glyph="face",Centers=Y, ... VarLabels=varNames,ObsLabels=Model(models77,:)); set(facePlot(:,1:2),Color="#D95319") title("1977 Model Year")

在此图中,两个最明显的特征是面孔大小和前额/下巴相对大小,这两个特征分别对应 MPG 和加速度变量。前额形状和下巴形状分别对应排量变量和重量变量。两眼之间的宽度对应马力变量。请注意,前额宽下巴窄的面孔很少,前额窄下巴宽的面孔也很少,这表明排量和重量正线性相关。此结果与从散点图矩阵得到的结果一致。
另请参阅
gplotmatrix | parallelcoords | andrewsplot | glyphplot