andrewsplot

创建安德鲁斯图来可视化分组的样本数据。

加载 fisheriris 数据集，该数据集包含三个鸢尾花品种的四个测量值（萼片长度、萼片宽度、花瓣长度和花瓣宽度）。

load fisheriris

矩阵 meas 包含 150 朵花的所有四个测量值。元胞数组 species 包含 150 朵花中每朵花的品种名称。

创建一个安德鲁斯图，按 species 对样本数据分组。

andrewsplot(meas,Group=species)

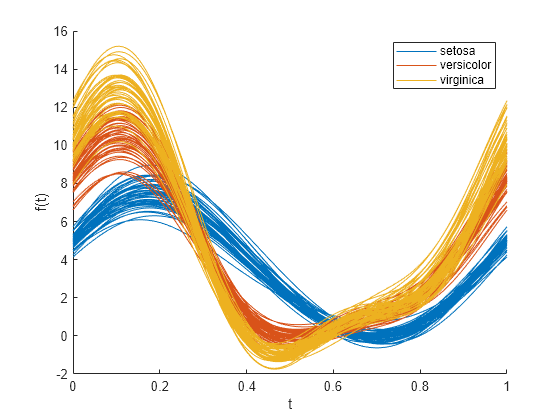
图将每个观测值（花朵）显示为区间 [0,1] 内的平滑函数。每条曲线的颜色对应不同花卉品种。

创建另一个简化的安德鲁斯图，仅显示每组的中位数和四分位数。

andrewsplot(meas,Group=species,Quantile=0.25)

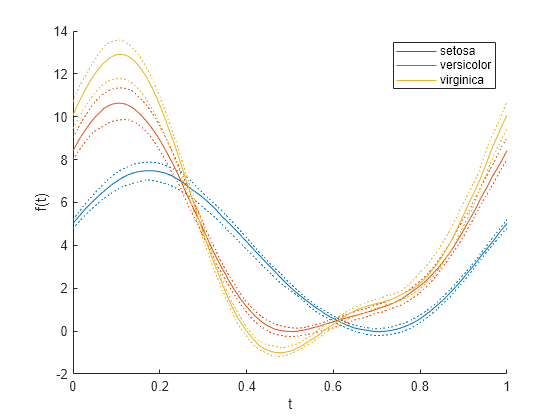
图将每组的中位数值显示为实曲线，将其他四分位数的值显示为相同颜色的虚曲线。

使用安德鲁斯图可视化多维数据。首先，将数据分组。然后，使用标准化和四分位数来查看各组之间的差异。

加载 patients 数据集，其中包含 100 位患者的医疗信息。指定描述性的类别名称 Smoker 和 Nonsmoker，而不是 1 和 0。然后，使用 Diastolic、Systolic、Weight、Age 和 Smoker 变量创建一个表。

load patients
Smoker = categorical(Smoker,logical([1 0]), ...
    ["Smoker","Nonsmoker"]);
patientData = table(Diastolic,Systolic,Weight,Age,Smoker);

基于 patientData 中的变量创建一个安德鲁斯图。使用最后一个变量按是否为吸烟者对数据进行分组。

andrewsplot(patientData{:,1:end-1},Group=patientData.Smoker)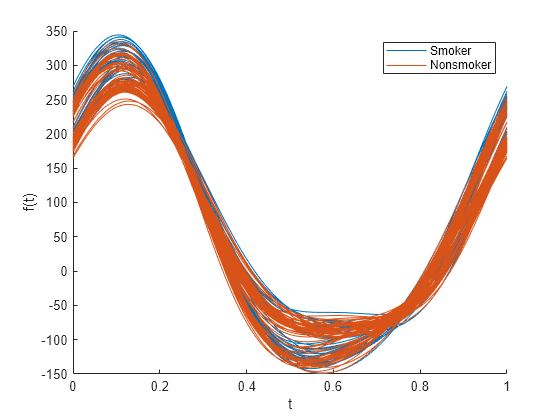

默认情况下，图使用未标准化数据。图显示 Smoker 组和 Nonsmoker 组之间没有巨大差异。

在绘图前标准化数值 patientData 变量。

andrewsplot(patientData{:,1:end-1},Group=Smoker,Standardize="on")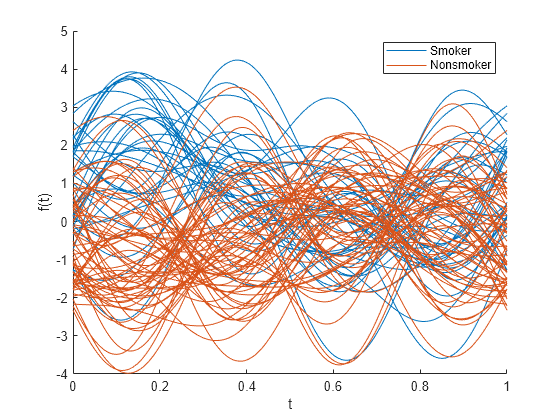

生成的安德鲁斯图显示 Smoker 和 Nonsmoker 组之间的更多差异。该图略显拥挤，因为它显示 100 条曲线，每条曲线对应于 patientData 中的一位患者。

它并不针对每个观测值显示一条曲线，而是针对每个组显示四分位数曲线。这些四分位数包括第 25 个百分位数、中位数和第 75 个百分位数。

andrewsplot(patientData{:,1:end-1},Group=patientData.Smoker, ...
    Standardize="on",Quantile=0.25)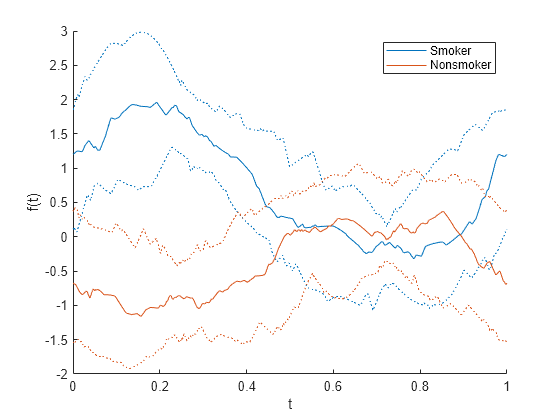

四分位数曲线显示 Smoker 组和 Nonsmoker 组之间的差异。例如，在大约 0.25 处，这两个组具有不重叠的四分位数值。

前面提到，安德鲁斯图中显示的每个函数均为变量的线性组合，其系数随时间而变化。（请参阅安德鲁斯图。）计算在时间 0.25 处变量的系数。变量的这种线性组合可以帮助您区分各组。

t = 0.25;
variables = patientData.Properties.VariableNames(1:end-1)

variables = 1×4 cell
    {'Diastolic'}    {'Systolic'}    {'Weight'}    {'Age'}

coefficients = [1/sqrt(2) sin(2*pi*t) cos(2*pi*t) sin(4*pi*t)]

coefficients = 1×4

    0.7071    1.0000    0.0000    0.0000

在时间 0.25 处，Diastolic 和 Systolic 变量具有相似幅值的正系数，Weight 和 Age 变量具有值为 0 的系数。前面的图显示，在数据标准化后，Smoker 组的四分位数曲线在时间 0.25 处具有正值，Nonsmoker 组的四分位数曲线在时间 0.25 处具有负值。

图和变量系数表明 Smoker 组中的患者往往具有更高的 Diastolic 和 Systolic 值，从而提供了一种在 patientData 中区分 Smoker 组和 Nonsmoker 组的方法。

调整安德鲁斯图的外观。您可以在对 andrewsplot 的调用中设置一些绘图属性。还可以在创建绘图之前或之后指定绘图的外观。

加载 fisheriris 数据集，该数据集包含三个鸢尾花品种的四个测量值（萼片长度、萼片宽度、花瓣长度和花瓣宽度）。

load fisheriris

矩阵 meas 包含 150 朵花的所有四个测量值。元胞数组 species 包含 150 朵花中每朵花的品种名称。

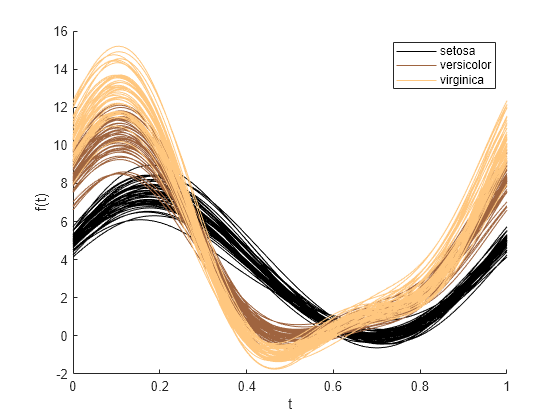
使用 meas 中的测量数据和 species 中的组数据创建一个安德鲁斯图。通过在绘制前设置色序，为分组数据指定非默认颜色方案 (copper)。

colororder(copper(3))
andrewsplot(meas,Group=species)

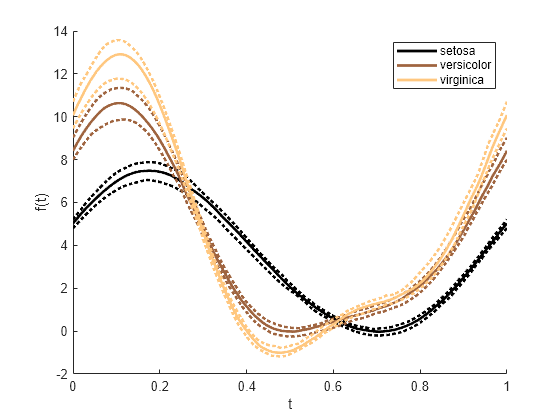
仅绘制 species 中每组的中位数、第 25 个百分位数和第 75 个百分位数的曲线。要使绘图线条变粗，请将线宽指定为 2。当您在对 andrewsplot 的调用中指定 LineWidth 值时，该函数会将图中每条曲线的线宽设置为相同的值。

andrewsplot(meas,Group=species,Quantile=0.25,LineWidth=2)

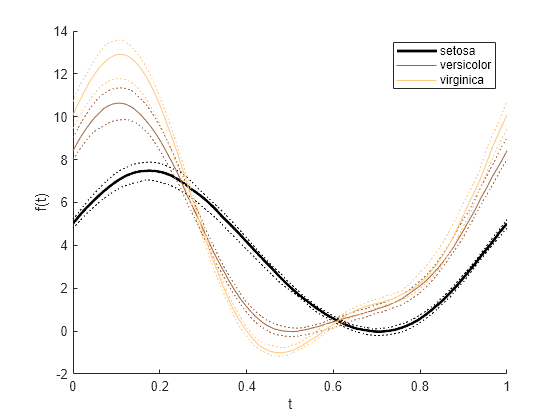
重新创建之前的绘图，但仅增大表示 setosa 组中鸢尾花测量值中位数的曲线的线宽。首先，创建一个由 Line 对象组成的数组 p，其中每个对象对应于绘图中的一条曲线。然后，使用圆点表示法修改数组中第一个 Line 对象的 LineWidth 属性。

p = andrewsplot(meas,Group=species,Quantile=0.25)

p = 
  9×1 Line array:

  Line    (median)
  Line    (lower quantile)
  Line    (upper quantile)
  Line    (median)
  Line    (lower quantile)
  Line    (upper quantile)
  Line    (median)
  Line    (lower quantile)
  Line    (upper quantile)

p(1).LineWidth = 2;