pca
原始数据的主成分分析
语法
说明
coeff = pca(X,Name,Value)Name,Value 对组参量指定的用于计算和处理特殊数据类型的附加选项,返回上述语法中的任何输出参量。
例如,您可以指定 pca 返回的主成分数或使用 SVD 以外的其他算法。
示例
加载样本数据集。
load hald原料数据有 4 个变量的 13 个观测值。
找出原料数据的主成分。
coeff = pca(ingredients)
coeff = 4×4
-0.0678 -0.6460 0.5673 0.5062
-0.6785 -0.0200 -0.5440 0.4933
0.0290 0.7553 0.4036 0.5156
0.7309 -0.1085 -0.4684 0.4844
coeff 的行包含四个原料变量的系数,其列对应于四个主成分。
当数据集中存在缺失值时,计算主成分系数。
加载样本数据集。
load imports-85数据矩阵 X 在第 3 列至第 15 列中有 13 个连续变量:轴距、长度、宽度、高度、整备重量、引擎大小、缸径、冲程、压缩比、马力、峰值转速、城市油耗和高速公路油耗。变量缸径和冲程在第 56 行至第 59 行中缺失四个值,变量马力和峰值转速在第 131 行和第 132 行中缺失两个值。
执行主成分分析。
coeff = pca(X(:,3:15));
默认情况下,pca 执行 'Rows','complete' 名称-值对组参量指定的操作。此选项在计算前会先删除包含 NaN 值的观测值。然后再将 NaN 行重新插入 score 和 tsquared 中的对应位置,即第 56 至 59、131 和 132 行。
使用 'pairwise' 执行主成分分析。
coeff = pca(X(:,3:15),'Rows','pairwise');
在本例中,pca 使用 X 的列 i 或 j 中没有 NaN 值的行来计算协方差矩阵的 (i,j) 元素。请注意,得到的协方差矩阵可能不是正定矩阵。当 pca 使用的算法是特征值分解时,此选项适用。当您没有指定算法时,如此示例中所示,pca 会将其设置为 'eig'。如果您需要 'svd' 作为算法并使用 'pairwise' 选项,则 pca 返回警告消息,将算法设置为 'eig' 并继续。
如果您使用 'Rows','all' 名称-值对组参量,pca 将终止,因为此选项假设数据集中没有缺失值。
coeff = pca(X(:,3:15),'Rows','all');
Error using pca (line 180) Raw data contains NaN missing value while 'Rows' option is set to 'all'. Consider using 'complete' or pairwise' option instead.
执行主成分分析时,使用变量的逆方差作为权重。
加载样本数据集。
load hald使用原料数据的逆方差作为变量权重执行主成分分析。
[wcoeff,~,latent,~,explained] = pca(ingredients,'VariableWeights','variance')
wcoeff = 4×4
-2.7998 2.9940 -3.9736 1.4180
-8.7743 -6.4411 4.8927 9.9863
2.5240 -3.8749 -4.0845 1.7196
9.1714 7.5529 3.2710 11.3273
latent = 4×1
2.2357
1.5761
0.1866
0.0016
explained = 4×1
55.8926
39.4017
4.6652
0.0406
请注意,系数矩阵 wcoeff 不是正交矩阵。
计算正交系数矩阵。
coefforth = diag(std(ingredients))\wcoeff
coefforth = 4×4
-0.4760 0.5090 -0.6755 0.2411
-0.5639 -0.4139 0.3144 0.6418
0.3941 -0.6050 -0.6377 0.2685
0.5479 0.4512 0.1954 0.6767
检查新系数矩阵 coefforth 的正交性。
coefforth*coefforth'
ans = 4×4
1.0000 0.0000 -0.0000 0.0000
0.0000 1.0000 0.0000 0
-0.0000 0.0000 1.0000 -0.0000
0.0000 0 -0.0000 1.0000
当数据中有缺失值时,使用交替最小二乘法 (ALS) 算法计算主成分。
加载样本数据。
load hald原料数据有 4 个变量的 13 个观测值。
使用 ALS 算法执行主成分分析,并显示成分系数。
[coeff,score,latent,tsquared,explained] = pca(ingredients); coeff
coeff = 4×4
-0.0678 -0.6460 0.5673 0.5062
-0.6785 -0.0200 -0.5440 0.4933
0.0290 0.7553 0.4036 0.5156
0.7309 -0.1085 -0.4684 0.4844
随机引入缺失值。
y = ingredients; rng('default'); % for reproducibility ix = random('unif',0,1,size(y))<0.30; y(ix) = NaN
y = 13×4
7 26 6 NaN
1 29 15 52
NaN NaN 8 20
11 31 NaN 47
7 52 6 33
NaN 55 NaN NaN
NaN 71 NaN 6
1 31 NaN 44
2 NaN NaN 22
21 47 4 26
NaN 40 23 34
11 66 9 NaN
10 68 8 12
⋮
NaN 指示,现在约有 30% 的数据包含缺失值。
使用 ALS 算法执行主成分分析,并显示成分系数。
[coeff1,score1,latent,tsquared,explained,mu1] = pca(y,... 'algorithm','als'); coeff1
coeff1 = 4×4
-0.0362 0.8215 -0.5252 0.2190
-0.6831 -0.0998 0.1828 0.6999
0.0169 0.5575 0.8215 -0.1185
0.7292 -0.0657 0.1261 0.6694
显示估计的均值。
mu1
mu1 = 1×4
8.9956 47.9088 9.0451 28.5515
重新构造观测到的数据。
t = score1*coeff1' + repmat(mu1,13,1)
t = 13×4
7.0000 26.0000 6.0000 51.5250
1.0000 29.0000 15.0000 52.0000
10.7819 53.0230 8.0000 20.0000
11.0000 31.0000 13.5500 47.0000
7.0000 52.0000 6.0000 33.0000
10.4818 55.0000 7.8328 17.9362
3.0982 71.0000 11.9491 6.0000
1.0000 31.0000 -0.5161 44.0000
2.0000 53.7914 5.7710 22.0000
21.0000 47.0000 4.0000 26.0000
21.5809 40.0000 23.0000 34.0000
11.0000 66.0000 9.0000 5.7078
10.0000 68.0000 8.0000 12.0000
⋮
ALS 算法估计数据中的缺失值。
另一种比较结果的方法是找出系数向量占据的两个空间之间的角度。使用 ALS 计算完整数据和含缺失值的数据的系数之间的角度。
subspace(coeff,coeff1)
ans = 8.7537e-16
这是一个很小的值。这表明,如果您在没有缺失数据的情况下使用 pca 和 'Rows','complete' 名称-值对组参量,而在有缺失数据的情况下使用 pca 和 'algorithm','als' 名称-值对组参量,结果彼此接近。
使用 'Rows','complete' 名称-值对组参量执行主成分分析,并显示成分系数。
[coeff2,score2,latent,tsquared,explained,mu2] = pca(y,... 'Rows','complete'); coeff2
coeff2 = 4×3
-0.2054 0.8587 0.0492
-0.6694 -0.3720 0.5510
0.1474 -0.3513 -0.5187
0.6986 -0.0298 0.6518
在本例中,pca 删除包含缺失值的行,而 y 只有四个行没有缺失值。pca 仅返回三个主成分。您无法使用 'Rows','pairwise' 选项,因为协方差矩阵不是半正定矩阵,pca 返回错误消息。
计算完整数据与整行删除缺失值数据(当 'Rows','complete' 时)的系数之间的角度。
subspace(coeff(:,1:3),coeff2)
ans = 0.3576
这两个空间之间的角度要大得多。这表明这两个结果不同。
显示估计的均值。
mu2
mu2 = 1×4
7.8889 46.9091 9.8750 29.6000
在本例中,均值只是 y 的样本均值。
重新构造观测到的数据。
score2*coeff2'
ans = 13×4
NaN NaN NaN NaN
-7.5162 -18.3545 4.0968 22.0056
NaN NaN NaN NaN
NaN NaN NaN NaN
-0.5644 5.3213 -3.3432 3.6040
NaN NaN NaN NaN
NaN NaN NaN NaN
NaN NaN NaN NaN
NaN NaN NaN NaN
12.8315 -0.1076 -6.3333 -3.7758
NaN NaN NaN NaN
NaN NaN NaN NaN
1.4680 20.6342 -2.9292 -18.0043
⋮
这表明删除包含 NaN 值的行的效果不如 ALS 算法。当数据有太多缺失值时,使用 ALS 更好。
计算主成分的系数、分数和方差。
加载样本数据集。
load hald原料数据有 4 个变量的 13 个观测值。
计算原料数据的成分的主成分系数、分数和方差。
[coeff,score,latent] = pca(ingredients)
coeff = 4×4
-0.0678 -0.6460 0.5673 0.5062
-0.6785 -0.0200 -0.5440 0.4933
0.0290 0.7553 0.4036 0.5156
0.7309 -0.1085 -0.4684 0.4844
score = 13×4
36.8218 -6.8709 -4.5909 0.3967
29.6073 4.6109 -2.2476 -0.3958
-12.9818 -4.2049 0.9022 -1.1261
23.7147 -6.6341 1.8547 -0.3786
-0.5532 -4.4617 -6.0874 0.1424
-10.8125 -3.6466 0.9130 -0.1350
-32.5882 8.9798 -1.6063 0.0818
22.6064 10.7259 3.2365 0.3243
-9.2626 8.9854 -0.0169 -0.5437
-3.2840 -14.1573 7.0465 0.3405
9.2200 12.3861 3.4283 0.4352
-25.5849 -2.7817 -0.3867 0.4468
-26.9032 -2.9310 -2.4455 0.4116
⋮
latent = 4×1
517.7969
67.4964
12.4054
0.2372
score 的每列对应一个主成分。向量 latent 存储四个主成分的方差。
重新构造中心化的原料数据。
Xcentered = score*coeff'
Xcentered = 13×4
-0.4615 -22.1538 -5.7692 30.0000
-6.4615 -19.1538 3.2308 22.0000
3.5385 7.8462 -3.7692 -10.0000
3.5385 -17.1538 -3.7692 17.0000
-0.4615 3.8462 -5.7692 3.0000
3.5385 6.8462 -2.7692 -8.0000
-4.4615 22.8462 5.2308 -24.0000
-6.4615 -17.1538 10.2308 14.0000
-5.4615 5.8462 6.2308 -8.0000
13.5385 -1.1538 -7.7692 -4.0000
-6.4615 -8.1538 11.2308 4.0000
3.5385 17.8462 -2.7692 -18.0000
2.5385 19.8462 -3.7692 -18.0000
⋮
Xcentered 中的新数据是将原始原料数据对应列减去列均值进行中心化后所得的结果。
在单一图中可视化每个变量的正交主成分系数和每个观测值的主成分分数。
biplot(coeff(:,1:2),'scores',score(:,1:2),'varlabels',{'v_1','v_2','v_3','v_4'});

所有四个变量在此双标图中都用向量来表示,向量的方向和长度指示每个变量对图中两个主成分的贡献。例如,位于水平轴上的第一个主成分对于第三个和第四个变量具有正系数。因此,向量 和 映射到图的右半部分。第一个主成分中最大的系数是第四个,对应于变量 。
第二个主成分位于垂直轴上,对于变量 、 和 具有负系数,对于变量 具有正系数。
该二维双标图还包含 13 个观测值的对应点,点在图中的坐标指示了每个观测值的两个主成分的分数。例如,绘图靠近左边缘的点对第一个主成分的分数最低。这些点基于最大分数值和最大系数长度进行了缩放,因此只能从图中确定其相对位置。
计算霍特林 T 方统计量值。
加载样本数据集。
load hald原料数据有 4 个变量的 13 个观测值。
执行主成分分析并请求 T 方值。
[coeff,score,latent,tsquared] = pca(ingredients); tsquared
tsquared = 13×1
5.6803
3.0758
6.0002
2.6198
3.3681
0.5668
3.4818
3.9794
2.6086
7.4818
4.1830
2.2327
2.7216
⋮
仅请求前两个主成分,并计算请求的主成分在降维空间中的 T 方值。
[coeff,score,latent,tsquared] = pca(ingredients,'NumComponents',2);
tsquaredtsquared = 13×1
5.6803
3.0758
6.0002
2.6198
3.3681
0.5668
3.4818
3.9794
2.6086
7.4818
4.1830
2.2327
2.7216
⋮
请注意,即使您指定了降维的成分空间,pca 仍会使用所有四个成分计算完整空间中的 T 方值。
降维空间中的 T 方值对应于降维空间中的马氏距离。
tsqreduced = mahal(score,score)
tsqreduced = 13×1
3.3179
2.0079
0.5874
1.7382
0.2955
0.4228
3.2457
2.6914
1.3619
2.9903
2.4371
1.3788
1.5251
⋮
通过求完整空间中的 T 方值和降维空间中的马氏距离之差来计算丢弃空间中的 T 方值。
tsqdiscarded = tsquared - tsqreduced
tsqdiscarded = 13×1
2.3624
1.0679
5.4128
0.8816
3.0726
0.1440
0.2362
1.2880
1.2467
4.4915
1.7459
0.8539
1.1965
⋮
计算主成分解释的变异性百分比。显示主成分空间中的数据表示。
加载样本数据集。
load imports-85数据矩阵 X 在第 3 列至第 15 列中有 13 个连续变量:轴距、长度、宽度、高度、整备重量、引擎大小、缸径、冲程、压缩比、马力、峰值转速、城市油耗和高速公路油耗。
计算由这些变量的主成分解释的变异性百分比。
[coeff,score,latent,tsquared,explained] = pca(X(:,3:15)); explained
explained = 13×1
64.3429
35.4484
0.1550
0.0379
0.0078
0.0048
0.0013
0.0011
0.0005
0.0002
0.0002
0.0000
0.0000
⋮
前三个成分解释所有变异性的 99.95%。
可视化前三个主成分的空间中的数据表示。
scatter3(score(:,1),score(:,2),score(:,3)) axis equal xlabel('1st Principal Component') ylabel('2nd Principal Component') zlabel('3rd Principal Component')
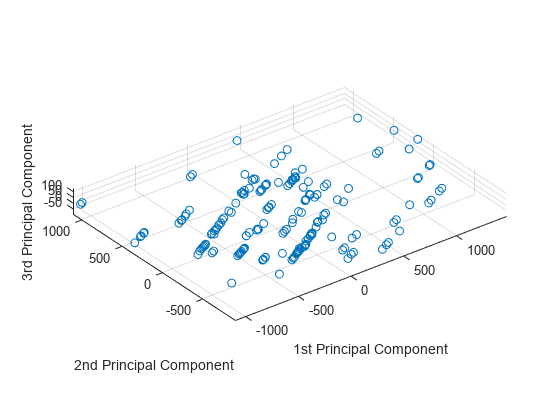
数据在第一主成分轴上具有最大变异性。在第一个轴的所有可能选择中,这是有可能得到的最大方差。在剩余可供第二主成分轴使用的所有可能选择中,该选择具有最大变异性。第三主成分轴具有第三大变异性,它显著小于在第二主成分轴上的变异性。第四至第十三主成分轴不值得研究,因为它们只解释数据中所有变异性的 0.05%。
要跳过任何输出,您可以在对应的元素中使用 ~。例如,如果您不想得到 T 方值,请指定
[coeff,score,latent,~,explained] = pca(X(:,3:15));
找出一个数据集的主成分,并将 PCA 应用于另一个数据集。当您有用于机器学习模型的训练数据集和测试数据集时,此过程非常有用。例如,您可以使用 PCA 对训练数据集进行预处理,然后训练模型。要使用测试数据集测试训练模型,您需要将从训练数据获得的 PCA 转换应用于测试数据集。
此示例还说明如何生成 C/C++ 代码。由于 pca 支持代码生成,因此您可以使用训练数据集生成执行 PCA 的代码,并将 PCA 应用于测试数据集。然后将代码部署到设备上。在此工作流中,您必须传递训练数据,训练数据有可能相当大。为了节省设备上的内存,您可以将训练和预测分离。在 MATLAB® 中使用 pca,并通过部署到设备上的生成代码对新数据应用 PCA。
生成 C/C++ 代码需要 MATLAB® Coder™。
将 PCA 应用于新数据
使用 readtable 将数据集加载到表中。数据集在文件 CreditRating_Historical.dat 中,其中包含历史信用评分数据。
creditrating = readtable('CreditRating_Historical.dat');
creditrating(1:5,:)ans=5×8 table
ID WC_TA RE_TA EBIT_TA MVE_BVTD S_TA Industry Rating
_____ _____ _____ _______ ________ _____ ________ _______
62394 0.013 0.104 0.036 0.447 0.142 3 {'BB' }
48608 0.232 0.335 0.062 1.969 0.281 8 {'A' }
42444 0.311 0.367 0.074 1.935 0.366 1 {'A' }
48631 0.194 0.263 0.062 1.017 0.228 4 {'BBB'}
43768 0.121 0.413 0.057 3.647 0.466 12 {'AAA'}
第一列是每个观测值的 ID,最后一列是评分。将第二列至第七列指定为预测变量数据,并将最后一列 (Rating) 指定为响应。
X = table2array(creditrating(:,2:7)); Y = creditrating.Rating;
使用前 100 个观测值作为测试数据,其余的作为训练数据。
XTest = X(1:100,:); XTrain = X(101:end,:); YTest = Y(1:100); YTrain = Y(101:end);
计算训练数据集 XTrain 的主成分。
[coeff,scoreTrain,~,~,explained,mu] = pca(XTrain);
此代码返回四个输出:coeff、scoreTrain、explained 和 mu。使用 explained(解释方差占总方差的百分比)计算解释至少 95% 变异性所需的成分的数目。使用 coeff(主成分系数)和 mu(XTrain 的估计均值)将 PCA 应用于测试数据集。在训练模型时,请使用 scoreTrain(主成分分数)而不是 XTrain。
显示由主成分解释的变异性百分比。
explained
explained = 6×1
58.2614
41.2606
0.3875
0.0632
0.0269
0.0005
前两个成分解释了 95% 以上的变异性。计算解释至少 95% 变异性所需的成分的数目。
idx = find(cumsum(explained)>95,1)
idx = 2
使用前两个成分训练分类树。
scoreTrain95 = scoreTrain(:,1:idx); mdl = fitctree(scoreTrain95,YTrain);
mdl 是一个 ClassificationTree 模型。
要对测试集使用训练模型,您需要使用从训练数据集获得的 PCA 来转换测试数据集。通过从 XTest 中减去 mu 再乘以 coeff 获得测试数据集的主成分分数。只需要前两个成分的分数,因此使用前两个系数 coeff(:,1:idx)。
scoreTest95 = (XTest-mu)*coeff(:,1:idx);
将经过训练的模型 mdl 和转换后的测试数据集 scoreTest 传递给 predict 函数,以预测测试集的评分。
YTest_predicted = predict(mdl,scoreTest95);
生成代码
生成代码,这些代码将 PCA 应用于数据并使用经过训练的模型预测评分。请注意,生成 C/C++ 代码需要 MATLAB® Coder™。
使用 saveLearnerForCoder 将分类模型保存到文件 myMdl.mat 中。
saveLearnerForCoder(mdl,'myMdl');定义名为 myPCAPredict 的入口函数,该函数接受测试数据集 (XTest) 和 PCA 信息(coeff 和 mu),并返回测试数据的评分。
在入口函数的函数签名后面添加 %#codegen 编译器指令(即 pragma),以指示您要为此 MATLAB 算法生成代码。添加此指令指示 MATLAB 代码分析器帮助您诊断和修复在代码生成过程中可能导致错误的违规。
function label = myPCAPredict(XTest,coeff,mu) %#codegen % Transform data using PCA scoreTest = bsxfun(@minus,XTest,mu)*coeff; % Load trained classification model mdl = loadLearnerForCoder('myMdl'); % Predict ratings using the loaded model label = predict(mdl,scoreTest);
myPCAPredict 使用 coeff 和 mu 将 PCA 应用于新数据,然后使用转换后的数据预测评分。这样,您就不必传递有可能特别大的训练数据。
注意:如果您点击位于此页右上角的按钮,并在 MATLAB® 中打开此示例,则 MATLAB® 将打开示例文件夹。该文件夹包括入口函数文件。
使用 codegen (MATLAB Coder) 生成代码。由于 C 和 C++ 是静态类型语言,因此必须在编译时确定入口函数中所有变量的属性。要指定数据类型和精确的输入数组大小,请使用 -args 选项传递表示具有特定数据类型和数组大小的值集的 MATLAB® 表达式。如果在编译时观测值数目未知,您也可以使用 coder.typeof (MATLAB Coder) 将输入指定为可变大小。有关详细信息,请参阅 Specify Variable-Size Arguments for Code Generation。
codegen myPCAPredict -args {coder.typeof(XTest,[Inf,6],[1,0]),coeff(:,1:idx),mu}
Code generation successful.
codegen 生成 MEX 函数 myPCAPredict_mex,扩展名因平台而异。
验证生成的代码。
YTest_predicted_mex = myPCAPredict_mex(XTest,coeff(:,1:idx),mu); isequal(YTest_predicted,YTest_predicted_mex)
ans = logical
1
isequal 返回逻辑值 1 (true),这意味着所有输入都相等。比较结果证实,mdl 的 predict 函数和 myPCAPredict_mex 函数返回相同的评分。
有关代码生成的详细信息,请参阅 Introduction to Code Generation 和 Generate Code at Command Line Using Model Exported from Machine Learning App。后者说明如何使用分类学习器执行 PCA 和训练模型,以及如何生成基于训练模型预测新数据标签的 C/C++ 代码。
输入参数
计算主成分时所基于的输入数据,指定为 n×p 矩阵。X 的行对应于观测值,列对应于变量。
数据类型: single | double
名称-值参数
将可选参量对组指定为 Name1=Value1,...,NameN=ValueN,其中 Name 是参量名称,Value 是对应的值。名称-值参量必须出现在其他参量之后,但对各个参量对组的顺序没有要求。
在 R2021a 之前,使用逗号分隔每个名称和值,并用引号将 Name 引起来。
示例: 'Algorithm','eig','Centered','off','Rows','all','NumComponents',3 指定 pca 使用特征值分解算法,不将数据中心化,使用所有观测值,并仅返回前三个主成分。
pca 用于执行主成分分析的主成分算法,指定为以逗号分隔的对组,其中包含 'Algorithm' 和以下项之一。
| 值 | 描述 |
|---|---|
'svd' | 默认值。X 的奇异值分解 (SVD)。 |
'eig' | 协方差矩阵的特征值分解 (EIG)。当观测值数目 n 超过变量的数目 p 时,EIG 算法比 SVD 更快,但不太准确,因为协方差的条件数是 X 的条件数的平方。 |
'als' | 交替最小二乘 (ALS) 算法。此算法通过将 ALS 能够更好地处理缺失值。它倾向于采用成对删除 ( |
示例: 'Algorithm','eig'
是否中心化列的指示符,指定为以逗号分隔的对组,其中包含 'Centered' 和下列逻辑表达式之一。
| 值 | 描述 |
|---|---|
on | 默认值。 |
off | 在这种情况下, |
示例: 'Centered',off
数据类型: logical
当自由度 d 小于变量数 p 时,是否精简输出的指示符,指定为以逗号分隔的对组,其中包含 'Economy' 和下列逻辑表达式之一。
| 值 | 描述 |
|---|---|
true | 默认值。 当变量的数目 p 远大于 d 时,此选项可以显著加快执行速度。 |
false |
|
请注意,当 d < p 时,score(:,d+1:p) 和 latent(d+1:p) 必须为零,且 coeff(:,d+1:p) 的列将定义与 X 正交的方向。
示例: 'Economy',false
数据类型: logical
要对数据矩阵 X 中的 NaN 值采取的操作,指定为以逗号分隔的对组,其中包含 'Rows' 和以下项之一。
| 值 | 描述 |
|---|---|
'complete' | 默认值。如果 |
'pairwise' | 此选项仅适用于算法为 当您指定 请注意,得到的协方差矩阵可能不是正定矩阵。在这种情况下, |
'all' |
|
示例: 'Rows','pairwise'
观测值权重,指定为以逗号分隔的对组,其中包含 'Weights',以及一个包含所有正元素的长度为 n 的向量。
数据类型: single | double
变量权重,指定为以逗号分隔的对组,其中包含 'VariableWeights' 和以下项之一。
| 值 | 描述 |
|---|---|
行向量 | 包含所有正元素的长度为 p 的向量。 |
'variance' | 变量权重是样本方差的倒数。如果您还使用 如果同时 |
示例: 'VariableWeights','variance'
数据类型: single | double | char | string
系数矩阵 coeff 的初始值,指定为以逗号分隔的对组,由 'Coeff0' 和 p×k 矩阵组成,其中 p 是变量的数目,k 是请求的主成分的数目。
注意
仅当 'algorithm' 是 'als' 时,才能使用此名称-值对组。
数据类型: single | double
分数矩阵 score 的初始值,指定为以逗号分隔的对组,由 'Score0' 和 n×k 矩阵组成,其中 n 是观测值的数目,k 是请求的主成分的数目。
注意
仅当 'algorithm' 是 'als' 时,才能使用此名称-值对组。
数据类型: single | double
迭代的选项,指定为以逗号分隔的对组,其中包含 'Options' 和由 statset 函数创建的结构体。pca 在 options 结构体中使用以下字段。
| 字段名称 | 描述 |
|---|---|
'Display' | 显示输出的级别。选项包括 'off'、'final' 和 'iter'。 |
'MaxIter' | 允许的最大步数。默认值为 1000。与优化设置不同,达到 MaxIter 值即视为收敛。 |
'TolFun' | 用来指定代价函数的终止容差的正数。默认值为 1e-6。 |
'TolX' | 正数,用来指定 ALS 算法中左因子矩阵和右因子矩阵的元素中相对变化的收敛阈值。默认值为 1e-6。 |
注意
仅当 'algorithm' 是 'als' 时,才能使用此名称-值对组。
您可以更改这些字段的值,并使用 'Options' 名称-值对组参量在 pca 中指定新结构体。
示例: opt = statset('pca'); opt.MaxIter = 2000; coeff = pca(X,'Options',opt);
数据类型: struct
输出参量
主成分系数,以 p×k 数值矩阵形式返回,其中 p=size(X,2)。如果 X 是 tall 数组,则 coeff 是 p×p 数值矩阵。有关详细信息,请参阅tall 数组。
当您指定 NumComponents 时,以下条件适用:
当您未指定 NumComponents 时,以下条件适用:
如果指定
Economy=true(默认值),则k等于自由度的数量。如果指定
Economy=false,则k等于p。
coeff 的每列都包含一个主成分的系数。这些列按主成分方差降序排列(请参阅 latent)。
主成分分数,以 n×k 数值矩阵形式返回,其中 n=size(X,1)。
当您指定 NumComponents 时,以下条件适用:
当您未指定 NumComponents 时,以下条件适用:
如果指定
Economy=true(默认值),则k等于自由度的数量。如果指定
Economy=false,则k等于size(X,2)。
score 的行对应于观测值,列对应于成分。
霍特林 T 方统计量(它是每个观测值的标准化分数的平方和)以长度为 size(X,2) 的数值列向量形式返回。
详细信息
霍特林 T 方统计量是每个观测值离数据集中心的多元距离的统计测度。
即使您请求的成分数目少于变量的数目,pca 也会使用所有主成分来计算 T 方统计量(在完整空间中计算它)。如果您需要计算降维空间或丢弃空间中的 T 方统计量,请执行以下操作之一:
要获得降维空间中的 T 方统计量,请使用
mahal(score,score)。要获得丢弃空间中的 T 方统计量,请首先使用
[coeff,score,latent,tsquared] = pca(X,'NumComponents',k,...)计算 T 方统计量,再使用tsqreduced = mahal(score,score)计算降维空间中的 T 方统计量,然后取差值:tsquared-tsqreduced。
如果数据经过中心化,则自由度 d 等于 i - 1,否则等于 i。
如果您指定
'Rows','complete',则 i 是X中不包含任何NaN的行的数目。如果您指定
'Rows','pairwise',则 i 是X中不包含NaN的行数最多的列对组中不包含任何NaN的行的数目。
请注意,当使用变量权重时,系数矩阵不是正交矩阵。假设您使用的变量权重向量称为 varwei,pca 返回的主成分系数向量为 wcoeff。则您可以使用转换 diag(sqrt(varwei))*wcoeff 来计算正交系数。
算法
pca 函数施加符号约定,强制 coefs 的每列中具有最大幅值的元素为正值。更改系数向量的符号并不更改其含义。
替代功能
App
要在实时编辑器中以交互方式运行 pca,请使用降低维度实时编辑器任务。
参考
[1] Jolliffe, I. T. Principal Component Analysis. 2nd ed., Springer, 2002.
[2] Krzanowski, W. J. Principles of Multivariate Analysis. Oxford University Press, 1988.
[3] Seber, G. A. F. Multivariate Observations. Wiley, 1984.
[4] Jackson, J. E. A. User's Guide to Principal Components. Wiley, 1988.
[5] Roweis, S. “EM Algorithms for PCA and SPCA.” In Proceedings of the 1997 Conference on Advances in Neural Information Processing Systems. Vol.10 (NIPS 1997), Cambridge, MA, USA: MIT Press, 1998, pp. 626–632.
[6] Ilin, A., and T. Raiko. “Practical Approaches to Principal Component Analysis in the Presence of Missing Values.” J. Mach. Learn. Res.. Vol. 11, August 2010, pp. 1957–2000.
扩展功能
此函数支持对无法放入内存的数据使用 tall 数组,但有一些限制。
pca通过计算协方差矩阵并使用内存pcacov函数计算主成分,直接处理 tall 数组。支持的语法包括:
coeff = pca(X)[coeff,score,latent] = pca(X)[coeff,score,latent,explained] = pca(X)[coeff,score,latent,tsquared] = pca(X)[coeff,score,latent,tsquared,explained] = pca(X)
如果
X是 tall 数组,则coeff是p×p数值矩阵,其中p=size(X,2)。不支持名称-值对组参量。
有关详细信息,请参阅使用 tall 数组处理无法放入内存的数据。
用法说明和限制:
当
'Algorithm'是'als'时,'Options'的'Display'值将被忽略。'Weights'和'VariableWeights'名称-值对组参量的值必须为实数。'Economy'名称-值对组参量的值必须为编译时常量。例如,要在生成的代码中使用'Economy',false名称-值对组参量,请在codegen(MATLAB Coder) 的-args值中包括{coder.Constant('Economy'),coder.Constant(false)}。名称-值参量中的名称必须为编译时常量。
生成的代码始终以列向量形式返回第五个输出
explained。生成的代码始终以行向量形式返回第六个输出
mu。如果
mu为空,pca会将mu以 1×0 数组形式返回。pca不会将mu转换为 0×0 空数组。生成的代码不会将包含所有
NaN值的输入矩阵X视为特例。输出维数与对应的有限输入项项数相当。为了节省部署生成代码的设备上的内存,可以将训练(基于输入数据构造 PCA 成分)和预测(执行 PCA 转换)分离。在 MATLAB® 中构造 PCA 成分。然后,定义入口函数,该函数使用
pca的输出,即主成分系数 (coeff) 和估计均值 (mu) 执行 PCA 转换。最后,为入口函数生成代码。有关示例,请参阅将 PCA 应用于新数据并生成 C/C++ 代码。
有关代码生成的详细信息,请参阅 Introduction to Code Generation 和 General Code Generation Workflow。
用法说明和限制:
您无法将名称-值参量
Algorithm指定为"als"。当变量数目很大时,EIG 算法通常比 SVD 要快。
有关详细信息,请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。
版本历史记录
在 R2012b 中推出
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)