fimplicit

Plot implicit symbolic equation or function

Syntax

fimplicit(f)

fimplicit(f,[min max])

fimplicit(f,[xmin xmax
ymin ymax])

fimplicit(___,LineSpec)

fimplicit(___,Name,Value)

fimplicit(ax,___)

fi = fimplicit(___)

Description

fimplicit(f) plots the implicit symbolic equation or function f over the default interval [-5 5] for x and y.

example

fimplicit(f,[min max]) plots f over the interval min < x < max and min < y < max.

fimplicit(f,[xmin xmax ymin ymax]) plots f over the interval xmin < x < xmax and ymin < y < ymax. The fimplicit function uses symvar to order the variables and assign intervals.

example

fimplicit(___,LineSpec) uses LineSpec to set the line style, marker symbol, and line color.

example

fimplicit(___,Name,Value) specifies line properties using one or more Name,Value pair arguments. Use this option with any of the input argument combinations in the previous syntaxes. Name,Value pair settings apply to all the lines plotted. To set options for individual lines, use the objects returned by fimplicit.

example

fimplicit(ax,___) plots into the axes specified by ax instead of the current axes gca.

fi = fimplicit(___) returns an implicit function line object. Use the object to query and modify properties of a specific line. For details, see ImplicitFunctionLine Properties.

example

Examples

collapse all

Plot Implicit Symbolic Equation

Open Live Script

Plot the hyperbola $x^{2} - y^{2} = 1$ by using fimplicit. The fimplicit function uses the default interval of $[- 5, 5]$ for $x$ and $y$ .

syms x y
fimplicit(x^2 - y^2 == 1)

Figure contains an axes object. The axes object contains an object of type implicitfunctionline.

Plot Implicit Symbolic Function

Open Live Script

Plot the hyperbola described by the function $f (x, y) = x^{2} - y^{2} - 1$ by first declaring the symbolic function f(x,y) using syms. The fimplicit function uses the default interval of $[- 5, 5]$ for $x$ and $y$ .

syms f(x,y)
f(x,y) = x^2 - y^2 - 1;
fimplicit(f)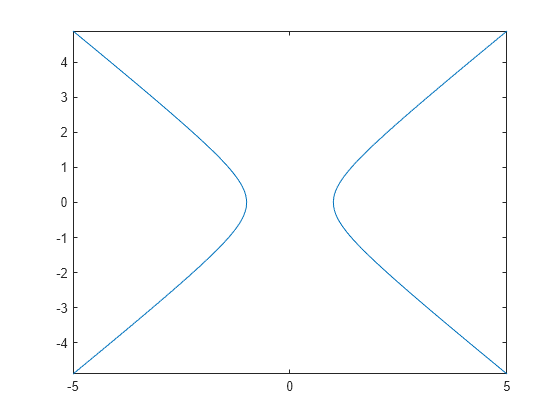

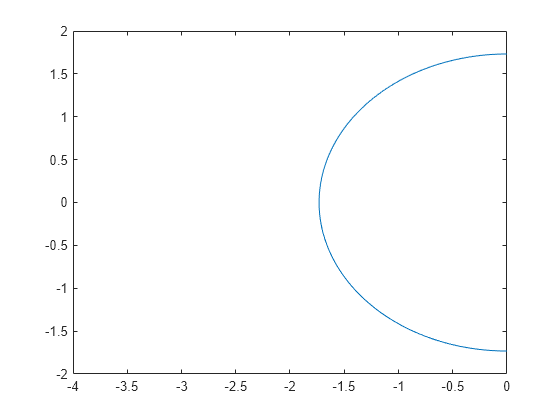
Figure contains an axes object. The axes object contains an object of type implicitfunctionline.

Specify Plotting Interval

Open Live Script

Plot half of the circle $x^{2} + y^{2} = 3$ by using the intervals $- 4 < x < 0$ and $- 2 < y < 2$ . Specify the plotting interval as the second argument of fimplicit.

syms x y
circle = x^2 + y^2 == 3;
fimplicit(circle, [-4 0 -2 2])

Figure contains an axes object. The axes object contains an object of type implicitfunctionline.

Plot Multiple Implicit Equations

Open Live Script

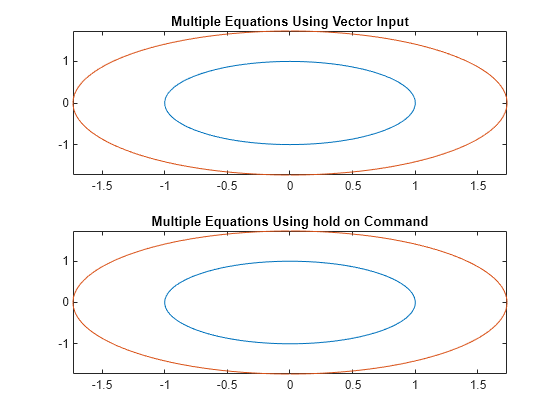
You can plot multiple equations either by passing the inputs as a vector or by using hold on to successively plot on the same figure. If you specify LineSpec and Name-Value arguments, they apply to all lines. To set options for individual plots, use the function handles returned by fimplicit.

Divide a figure into two subplots by using subplot. On the first subplot, plot $x^{2} + y^{2} = = 1$ and $x^{2} + y^{2} = = 3$ using vector input. On the second subplot, plot the same inputs by using hold on.

syms x y
circle1 = x^2 + y^2 == 1;
circle2 = x^2 + y^2 == 3;

subplot(2,1,1)
fimplicit([circle1 circle2])
title('Multiple Equations Using Vector Input')

subplot(2,1,2)
fimplicit(circle1)
hold on
fimplicit(circle2)
title('Multiple Equations Using hold on Command')

hold off

Figure contains 2 axes objects. Axes object 1 with title Multiple Equations Using Vector Input contains 2 objects of type implicitfunctionline. Axes object 2 with title Multiple Equations Using hold on Command contains 2 objects of type implicitfunctionline.

Change Line Properties and Display Markers

Open Live Script

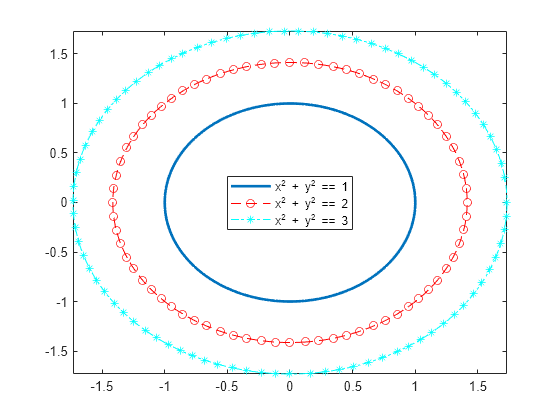
Plot three concentric circles of increasing diameter. For the first line, use a linewidth of 2. For the second, specify a dashed red line style with circle markers. For the third, specify a cyan, dash-dot line style with asterisk markers. Display the legend.

syms x y
circle = x^2 + y^2;
fimplicit(circle == 1, 'Linewidth', 2)
hold on
fimplicit(circle == 2, '--or')
fimplicit(circle == 3, '-.*c')
legend('show','Location','best')
hold off

Figure contains an axes object. The axes object contains 3 objects of type implicitfunctionline.

Modify Implicit Plot After Creation

Open Live Script

Plot $y \sin (x) + x \cos (y) = 1$ . Specify an output to make fimplicit return the plot object.

syms x y
eqn = y*sin(x) + x*cos(y) == 1;
fi = fimplicit(eqn)

Figure contains an axes object. The axes object contains an object of type implicitfunctionline.

fi = 
  ImplicitFunctionLine with properties:

     Function: x*cos(y) + y*sin(x) == 1
        Color: [0 0.4470 0.7410]
    LineStyle: '-'
    LineWidth: 0.5000

  Use GET to show all properties

Change the plotted equation to $x \cos (y) + y \sin (x) = 0$ by using dot notation to set properties. Similarly, change the line color to red and line style to a dash-dot line. The horizontal and vertical lines in the output are artifacts that should be ignored.

fi.Function = x/cos(y) + y/sin(x) == 0;
fi.Color = 'r';
fi.LineStyle = '-.';

Figure contains an axes object. The axes object contains an object of type implicitfunctionline.

Add Title and Axis Labels and Format Ticks

Open Live Script

Plot $x \cos (y) + y \sin (x) = 1$ over the interval $- 2 π < x < 2 π$ and $- 2 π < y < 2 π$ . Add a title and axis labels. Create the x-axis ticks by spanning the x-axis limits at intervals of pi/2. Display these ticks by using the XTick property. Create x-axis labels by using arrayfun to apply texlabel to S. Display these labels by using the XTickLabel property. Repeat these steps for the y-axis.

To use LaTeX in plots, see latex.

syms x y
eqn = x*cos(y) + y*sin(x) == 1;
fimplicit(eqn, [-2*pi 2*pi])
grid on
title('x cos(y) + y sin(x) for -2\pi < x < 2\pi and -2\pi < y < 2\pi')
xlabel('x')
ylabel('y')
ax = gca;

S = sym(ax.XLim(1):pi/2:ax.XLim(2));
ax.XTick = double(S);
ax.XTickLabel = arrayfun(@texlabel, S, 'UniformOutput', false);

S = sym(ax.YLim(1):pi/2:ax.YLim(2));
ax.YTick = double(S);
ax.YTickLabel = arrayfun(@texlabel, S, 'UniformOutput', false);

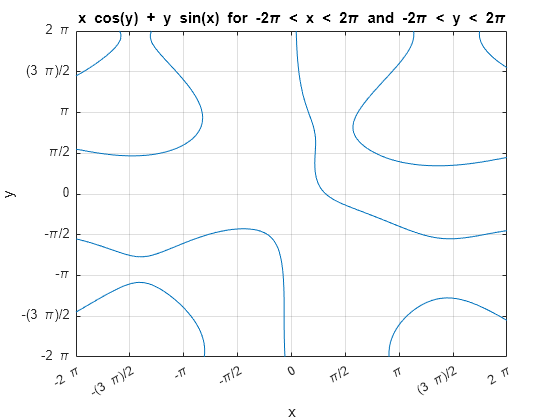
Figure contains an axes object. The axes object with title x cos(y) blank + blank y blank sin(x) blank for blank - 2 pi blank < blank x blank < blank 2 pi blank and blank - 2 pi blank < blank y blank < blank 2 pi, xlabel x, ylabel y contains an object of type implicitfunctionline.

Re-Evaluation on Zoom

Open Live Script

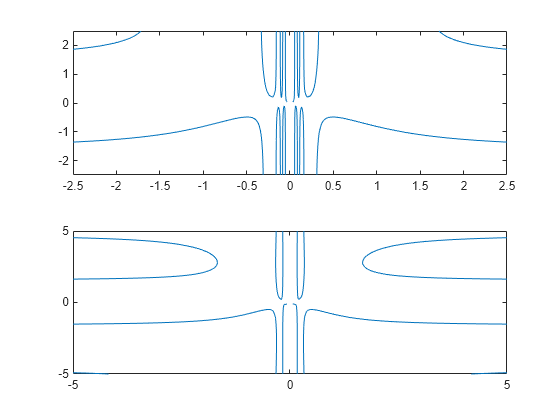
When you zoom into a plot, fimplicit re-evaluates the plot automatically. This re-evaluation on zoom can reveal hidden detail at smaller scales.

Divide a figure into two by using subplot. Plot $x \cos (y) + y \sin (1 / x) = 0$ in both the first and second subplots. Zoom into the second subplot by using zoom. The zoomed subplot shows detail that is not visible in the first subplot.

syms x y
eqn = x*cos(y) + y*sin(1/x) == 0;

subplot(2,1,1)
fimplicit(eqn)

subplot(2,1,2)
fimplicit(eqn)
zoom(2)

Figure contains 2 axes objects. Axes object 1 contains an object of type implicitfunctionline. Axes object 2 contains an object of type implicitfunctionline.

Input Arguments

collapse all

`f` — Implicit equation or function to plot
symbolic equation | symbolic expression | symbolic function

Implicit equation or function to plot, specified as a symbolic equation, expression, or function. If the right-hand side is not specified, then it is assumed to be 0.

`[min max]` — Plotting range for `x` and `y`
[–5 5] (default) | vector of two numbers

Plotting range for x and y, specified as a vector of two numbers. The default range is [-5 5].

`[xmin xmax ymin ymax]` — Plotting range for `x` and `y`
[–5 5 –5 5] (default) | vector of four numbers

Plotting range for x and y, specified as a vector of four numbers. The default range is [-5 5 -5 5].

`ax` — Axes object
axes object

Axes object. If you do not specify an axes object, then fimplicit uses the current axes gca.

`LineSpec` — Line style, marker, and color
string scalar | character vector

Line style, marker, and color, specified as a string scalar or character vector containing symbols. The symbols can appear in any order. You do not need to specify all three characteristics (line style, marker, and color). For example, if you omit the line style and specify the marker, then the plot shows only the marker and no line.

Example: "--or" is a red dashed line with circle markers.

Line Style	Description	Resulting Line
`"-"`	Solid line
`"--"`	Dashed line
`":"`	Dotted line
`"-."`	Dash-dotted line

Marker	Description	Resulting Marker
`"o"`	Circle
`"+"`	Plus sign
`"*"`	Asterisk
`"."`	Point
`"x"`	Cross
`"_"`	Horizontal line
`"\|"`	Vertical line
`"square"`	Square
`"diamond"`	Diamond
`"^"`	Upward-pointing triangle
`"v"`	Downward-pointing triangle
`">"`	Right-pointing triangle
`"<"`	Left-pointing triangle
`"pentagram"`	Pentagram
`"hexagram"`	Hexagram

Color Name	Short Name	RGB Triplet
`"red"`	`"r"`	`[1 0 0]`
`"green"`	`"g"`	`[0 1 0]`
`"blue"`	`"b"`	`[0 0 1]`
`"cyan"`	`"c"`	`[0 1 1]`
`"magenta"`	`"m"`	`[1 0 1]`
`"yellow"`	`"y"`	`[1 1 0]`
`"black"`	`"k"`	`[0 0 0]`
`"white"`	`"w"`	`[1 1 1]`

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Marker','o','MarkerFaceColor','red'

The function line properties listed here are only a subset. For a complete list, see ImplicitFunctionLine Properties.

`MeshDensity` — Number of evaluation points per direction
151 (default) | number

Number of evaluation points per direction, specified as a number. The default is 151.

`Color` — Line color
`[0 0.4470 0.7410]` (default) | RGB triplet | hexadecimal color code | `"r"` | `"g"` | `"b"` | ...

Line color, specified as an RGB triplet, a hexadecimal color code, a color name, or a short name.

For a custom color, specify an RGB triplet or a hexadecimal color code.

An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range [0,1], for example, [0.4 0.6 0.7].
A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (#) followed by three or six hexadecimal digits, which can range from 0 to F. The values are not case sensitive. Therefore, the color codes "#FF8800", "#ff8800", "#F80", and "#f80" are equivalent.

Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.

Color Name	Short Name	RGB Triplet	Hexadecimal Color Code
`"red"`	`"r"`	`[1 0 0]`	`"#FF0000"`
`"green"`	`"g"`	`[0 1 0]`	`"#00FF00"`
`"blue"`	`"b"`	`[0 0 1]`	`"#0000FF"`
`"cyan"`	`"c"`	`[0 1 1]`	`"#00FFFF"`
`"magenta"`	`"m"`	`[1 0 1]`	`"#FF00FF"`
`"yellow"`	`"y"`	`[1 1 0]`	`"#FFFF00"`
`"black"`	`"k"`	`[0 0 0]`	`"#000000"`
`"white"`	`"w"`	`[1 1 1]`	`"#FFFFFF"`

Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB^® uses in many types of plots.

RGB Triplet	Hexadecimal Color Code	Appearance
`[0 0.4470 0.7410]`	`"#0072BD"`
`[0.8500 0.3250 0.0980]`	`"#D95319"`
`[0.9290 0.6940 0.1250]`	`"#EDB120"`
`[0.4940 0.1840 0.5560]`	`"#7E2F8E"`
`[0.4660 0.6740 0.1880]`	`"#77AC30"`
`[0.3010 0.7450 0.9330]`	`"#4DBEEE"`
`[0.6350 0.0780 0.1840]`	`"#A2142F"`

Example: "blue"

Example: [0 0 1]

Example: "#0000FF"

`LineStyle` — Line style
`"-"` (default) | `"--"` | `":"` | `"-."` | `"none"`

Line style, specified as one of the options listed in this table.

Line Style	Description	Resulting Line
`"-"`	Solid line
`"--"`	Dashed line
`":"`	Dotted line
`"-."`	Dash-dotted line
`"none"`	No line	No line

`LineWidth` — Line width
`0.5` (default) | positive value

Line width, specified as a positive value in points, where 1 point = 1/72 of an inch. If the line has markers, then the line width also affects the marker edges.

The line width cannot be thinner than the width of a pixel. If you set the line width to a value that is less than the width of a pixel on your system, the line displays as one pixel wide.

`Marker` — Marker symbol
`"none"` (default) | `"o"` | `"+"` | `"*"` | `"."` | ...

Marker symbol, specified as one of the values listed in this table. By default, the object does not display markers. Specifying a marker symbol adds markers at each data point or vertex.

Marker	Description	Resulting Marker
`"o"`	Circle
`"+"`	Plus sign
`"*"`	Asterisk
`"."`	Point
`"x"`	Cross
`"_"`	Horizontal line
`"\|"`	Vertical line
`"square"`	Square
`"diamond"`	Diamond
`"^"`	Upward-pointing triangle
`"v"`	Downward-pointing triangle
`">"`	Right-pointing triangle
`"<"`	Left-pointing triangle
`"pentagram"`	Pentagram
`"hexagram"`	Hexagram
`"none"`	No markers	Not applicable

`MarkerEdgeColor` — Marker outline color
`"auto"` (default) | RGB triplet | hexadecimal color code | `"r"` | `"g"` | `"b"` | ...

Marker outline color, specified as "auto", an RGB triplet, a hexadecimal color code, a color name, or a short name. The default value of "auto" uses the same color as the Color property.

For a custom color, specify an RGB triplet or a hexadecimal color code.

An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range [0,1], for example, [0.4 0.6 0.7].
A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (#) followed by three or six hexadecimal digits, which can range from 0 to F. The values are not case sensitive. Therefore, the color codes "#FF8800", "#ff8800", "#F80", and "#f80" are equivalent.

Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.

Color Name	Short Name	RGB Triplet	Hexadecimal Color Code	Appearance
`"red"`	`"r"`	`[1 0 0]`	`"#FF0000"`
`"green"`	`"g"`	`[0 1 0]`	`"#00FF00"`
`"blue"`	`"b"`	`[0 0 1]`	`"#0000FF"`
`"cyan"`	`"c"`	`[0 1 1]`	`"#00FFFF"`
`"magenta"`	`"m"`	`[1 0 1]`	`"#FF00FF"`
`"yellow"`	`"y"`	`[1 1 0]`	`"#FFFF00"`
`"black"`	`"k"`	`[0 0 0]`	`"#000000"`
`"white"`	`"w"`	`[1 1 1]`	`"#FFFFFF"`
`"none"`	Not applicable	Not applicable	Not applicable	No color

Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB uses in many types of plots.

RGB Triplet	Hexadecimal Color Code	Appearance
`[0 0.4470 0.7410]`	`"#0072BD"`
`[0.8500 0.3250 0.0980]`	`"#D95319"`
`[0.9290 0.6940 0.1250]`	`"#EDB120"`
`[0.4940 0.1840 0.5560]`	`"#7E2F8E"`
`[0.4660 0.6740 0.1880]`	`"#77AC30"`
`[0.3010 0.7450 0.9330]`	`"#4DBEEE"`
`[0.6350 0.0780 0.1840]`	`"#A2142F"`

`MarkerFaceColor` — Marker fill color
`"none"` (default) | `"auto"` | RGB triplet | hexadecimal color code | `"r"` | `"g"` | `"b"` | ...

Marker fill color, specified as "auto", an RGB triplet, a hexadecimal color code, a color name, or a short name. The "auto" value uses the same color as the MarkerEdgeColor property.

For a custom color, specify an RGB triplet or a hexadecimal color code.

An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range [0,1], for example, [0.4 0.6 0.7].
A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (#) followed by three or six hexadecimal digits, which can range from 0 to F. The values are not case sensitive. Therefore, the color codes "#FF8800", "#ff8800", "#F80", and "#f80" are equivalent.

Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.

Color Name	Short Name	RGB Triplet	Hexadecimal Color Code	Appearance
`"red"`	`"r"`	`[1 0 0]`	`"#FF0000"`
`"green"`	`"g"`	`[0 1 0]`	`"#00FF00"`
`"blue"`	`"b"`	`[0 0 1]`	`"#0000FF"`
`"cyan"`	`"c"`	`[0 1 1]`	`"#00FFFF"`
`"magenta"`	`"m"`	`[1 0 1]`	`"#FF00FF"`
`"yellow"`	`"y"`	`[1 1 0]`	`"#FFFF00"`
`"black"`	`"k"`	`[0 0 0]`	`"#000000"`
`"white"`	`"w"`	`[1 1 1]`	`"#FFFFFF"`
`"none"`	Not applicable	Not applicable	Not applicable	No color

Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB uses in many types of plots.

RGB Triplet	Hexadecimal Color Code	Appearance
`[0 0.4470 0.7410]`	`"#0072BD"`
`[0.8500 0.3250 0.0980]`	`"#D95319"`
`[0.9290 0.6940 0.1250]`	`"#EDB120"`
`[0.4940 0.1840 0.5560]`	`"#7E2F8E"`
`[0.4660 0.6740 0.1880]`	`"#77AC30"`
`[0.3010 0.7450 0.9330]`	`"#4DBEEE"`
`[0.6350 0.0780 0.1840]`	`"#A2142F"`

Example: [0.3 0.2 0.1]

Example: "green"

Example: "#D2F9A7"

`MarkerSize` — Marker size
`6` (default) | positive value

Marker size, specified as a positive value in points, where 1 point = 1/72 of an inch.

Output Arguments

collapse all

`fi` — One or more implicit function line objects
scalar | vector

One or more implicit function line objects, returned as a scalar or a vector. You can use these objects to query and modify properties of a specific line. For a list of properties, see ImplicitFunctionLine Properties.

Algorithms

fimplicit assigns the symbolic variables in f to the x-axis, then the y-axis, and symvar determines the order of the variables to be assigned. Therefore, variable and axis names might not correspond. To force fimplicit to assign x or y to its corresponding axis, create the symbolic function to plot, then pass the symbolic function to fimplicit.

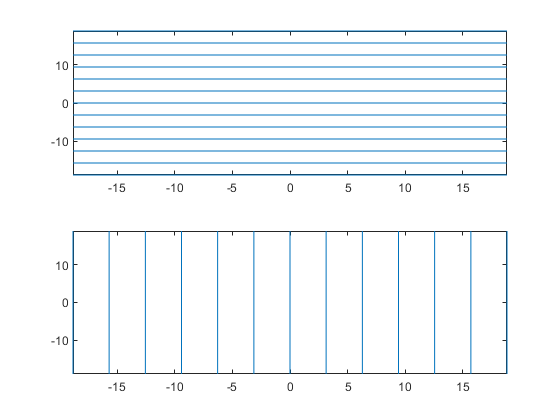
For example, the following code plots the roots of the implicit function f(x,y) = sin(y) in two ways. The first way forces the waves to oscillate with respect to the y-axis. In other words, the first plot assigns the y variable to the corresponding y-axis. The second plot assigns y to the x-axis because it is the first (and only) variable in the symbolic function.

syms x y;
f(x,y) = sin(y);
intvl = [-6 6]*pi;

figure;
subplot(2,1,1)
fimplicit(f,intvl);
subplot(2,1,2)
fimplicit(f(x,y),intvl); % Or fimplicit(sin(y) == 0,intvl);

Two plots showing waves that oscillate, one plot with respect to the y-axis and the other plot with respect to the x-axis

Version History

Introduced in R2016b

fimplicit

Syntax

Description

Examples

Plot Implicit Symbolic Equation

Plot Implicit Symbolic Function

Specify Plotting Interval

Plot Multiple Implicit Equations

Change Line Properties and Display Markers

Modify Implicit Plot After Creation

Add Title and Axis Labels and Format Ticks

Re-Evaluation on Zoom

Input Arguments

`f` — Implicit equation or function to plot
symbolic equation | symbolic expression | symbolic function

`[min max]` — Plotting range for `x` and `y`
[–5 5] (default) | vector of two numbers

`[xmin xmax ymin ymax]` — Plotting range for `x` and `y`
[–5 5 –5 5] (default) | vector of four numbers

`ax` — Axes object
axes object

`LineSpec` — Line style, marker, and color
string scalar | character vector

Name-Value Arguments

`MeshDensity` — Number of evaluation points per direction
151 (default) | number

`Color` — Line color
`[0 0.4470 0.7410]` (default) | RGB triplet | hexadecimal color code | `"r"` | `"g"` | `"b"` | ...

`LineStyle` — Line style
`"-"` (default) | `"--"` | `":"` | `"-."` | `"none"`

`LineWidth` — Line width
`0.5` (default) | positive value

`Marker` — Marker symbol
`"none"` (default) | `"o"` | `"+"` | `"*"` | `"."` | ...

`MarkerEdgeColor` — Marker outline color
`"auto"` (default) | RGB triplet | hexadecimal color code | `"r"` | `"g"` | `"b"` | ...

`MarkerFaceColor` — Marker fill color
`"none"` (default) | `"auto"` | RGB triplet | hexadecimal color code | `"r"` | `"g"` | `"b"` | ...

`MarkerSize` — Marker size
`6` (default) | positive value

Output Arguments

`fi` — One or more implicit function line objects
scalar | vector

Algorithms

Version History

See Also

Functions

Properties

Topics

fimplicit

Syntax

Description

Examples

Plot Implicit Symbolic Equation

Plot Implicit Symbolic Function

Specify Plotting Interval

Plot Multiple Implicit Equations

Change Line Properties and Display Markers

Modify Implicit Plot After Creation

Add Title and Axis Labels and Format Ticks

Re-Evaluation on Zoom

Input Arguments

f — Implicit equation or function to plot symbolic equation | symbolic expression | symbolic function

[min max] — Plotting range for x and y [–5 5] (default) | vector of two numbers

[xmin xmax ymin ymax] — Plotting range for x and y [–5 5 –5 5] (default) | vector of four numbers

ax — Axes object axes object

LineSpec — Line style, marker, and color string scalar | character vector

Name-Value Arguments

MeshDensity — Number of evaluation points per direction 151 (default) | number

Color — Line color [0 0.4470 0.7410] (default) | RGB triplet | hexadecimal color code | "r" | "g" | "b" | ...

LineStyle — Line style "-" (default) | "--" | ":" | "-." | "none"

LineWidth — Line width 0.5 (default) | positive value

Marker — Marker symbol "none" (default) | "o" | "+" | "*" | "." | ...

MarkerEdgeColor — Marker outline color "auto" (default) | RGB triplet | hexadecimal color code | "r" | "g" | "b" | ...

MarkerFaceColor — Marker fill color "none" (default) | "auto" | RGB triplet | hexadecimal color code | "r" | "g" | "b" | ...

MarkerSize — Marker size 6 (default) | positive value

Output Arguments

fi — One or more implicit function line objects scalar | vector

Algorithms

Version History

See Also

Functions

Properties

Topics

`f` — Implicit equation or function to plot
symbolic equation | symbolic expression | symbolic function

`[min max]` — Plotting range for `x` and `y`
[–5 5] (default) | vector of two numbers

`[xmin xmax ymin ymax]` — Plotting range for `x` and `y`
[–5 5 –5 5] (default) | vector of four numbers

`ax` — Axes object
axes object

`LineSpec` — Line style, marker, and color
string scalar | character vector

`MeshDensity` — Number of evaluation points per direction
151 (default) | number

`Color` — Line color
`[0 0.4470 0.7410]` (default) | RGB triplet | hexadecimal color code | `"r"` | `"g"` | `"b"` | ...

`LineStyle` — Line style
`"-"` (default) | `"--"` | `":"` | `"-."` | `"none"`

`LineWidth` — Line width
`0.5` (default) | positive value

`Marker` — Marker symbol
`"none"` (default) | `"o"` | `"+"` | `"*"` | `"."` | ...

`MarkerEdgeColor` — Marker outline color
`"auto"` (default) | RGB triplet | hexadecimal color code | `"r"` | `"g"` | `"b"` | ...

`MarkerFaceColor` — Marker fill color
`"none"` (default) | `"auto"` | RGB triplet | hexadecimal color code | `"r"` | `"g"` | `"b"` | ...

`MarkerSize` — Marker size
`6` (default) | positive value

`fi` — One or more implicit function line objects
scalar | vector