求解微分方程组

使用 dsolve 函数（可以指定初始条件，也可以不指定初始条件）求解包含多个变量的由多个常微分方程组成的方程组。要求解单个微分方程，请参阅求解微分方程。

求解微分方程组

求解以下一阶线性微分方程组。

$\begin{array}{l} \frac{du}{dt} = 3 u + 4 v, \\ \frac{dv}{dt} = - 4 u + 3 v . \end{array}$

首先，通过使用 syms 创建符号函数 u(t) 和 v(t)，来表示 $u$ 和 $v$ 。

syms u(t) v(t)

使用 == 定义方程，并使用 diff 函数表示微分。

ode1 = diff(u) == 3*u + 4*v;
ode2 = diff(v) == -4*u + 3*v;
odes = [ode1; ode2]

odes(t) = 
 $(\begin{array}{c} \frac{\partial}{\partial t} u (t) = 3 u (t) + 4 v (t) \\ \frac{\partial}{\partial t} v (t) = 3 v (t) - 4 u (t) \end{array})$

使用 dsolve 函数求解该方程组，它会以结构体的元素形式返回解。

S = dsolve(odes)

S = struct with fields:
    v: C1*cos(4*t)*exp(3*t) - C2*sin(4*t)*exp(3*t)
    u: C2*cos(4*t)*exp(3*t) + C1*sin(4*t)*exp(3*t)

如果 dsolve 无法求解方程，则尝试以数值方式求解方程。请参阅Solve a Second-Order Differential Equation Numerically。

要获得 u(t) 和 v(t)，请对结构体 S 进行索引。

uSol(t) = S.u

uSol(t) =  $C_{2} \cos (4 t) e^{3 t} + C_{1} \sin (4 t) e^{3 t}$

vSol(t) = S.v

vSol(t) =  $C_{1} \cos (4 t) e^{3 t} - C_{2} \sin (4 t) e^{3 t}$

或者，通过提供多个输出参量直接存储 u(t) 和 v(t)。

[uSol(t),vSol(t)] = dsolve(odes)

uSol(t) =  $C_{2} \cos (4 t) e^{3 t} + C_{1} \sin (4 t) e^{3 t}$

vSol(t) =  $C_{1} \cos (4 t) e^{3 t} - C_{2} \sin (4 t) e^{3 t}$

由于未指定条件，因此解中出现了常数 C1 和 C2。在指定初始条件 u(0) == 0 和 v(0) == 0 的情况下求解该方程组。dsolve 函数会求出满足这些条件的常数的值。

cond1 = u(0) == 0;
cond2 = v(0) == 1;
conds = [cond1; cond2];
[uSol(t),vSol(t)] = dsolve(odes,conds)

uSol(t) =  $\sin (4 t) e^{3 t}$

vSol(t) =  $\cos (4 t) e^{3 t}$

使用 fplot 绘制解的图。

fplot(uSol)
hold on
fplot(vSol)
grid on
legend("uSol","vSol",Location="best")

Figure contains an axes object. The axes object contains 2 objects of type functionline. These objects represent uSol, vSol.

求解矩阵形式的微分方程

使用 dsolve 求解矩阵形式的微分方程。

以下面这个微分方程组为例。

$\begin{array}{l} \frac{dx}{dt} = x + 2 y + 1, \\ \frac{dy}{dt} = - x + y + t . \end{array}$

该方程组的矩阵形式为

$[\begin{array}{c} x^{'} \\ y^{'} \end{array}] = [\begin{array}{c} 1 & 2 \\ - 1 & 1 \end{array}] [\begin{array}{c} x \\ y \end{array}] + [\begin{array}{c} 1 \\ t \end{array}] .$

设

$Y = [\begin{array}{c} x \\ y \end{array}], A = [\begin{array}{c} 1 & 2 \\ - 1 & 1 \end{array}], B = [\begin{array}{c} 1 \\ t \end{array}] .$

此时方程组变为 $Y^{'} = A Y + B .$ 。

定义这些矩阵和矩阵方程。

syms x(t) y(t)
A = [1 2; -1 1];
B = [1; t];
Y = [x; y];
odes = diff(Y) == A*Y + B

odes(t) = 
 $(\begin{array}{c} \frac{\partial}{\partial t} x (t) = x (t) + 2 y (t) + 1 \\ \frac{\partial}{\partial t} y (t) = t - x (t) + y (t) \end{array})$

使用 dsolve 求解矩阵方程。使用 simplify 函数简化解。

[xSol(t),ySol(t)] = dsolve(odes);
xSol(t) = simplify(xSol(t))

xSol(t) = 
 $\frac{2 t}{3} + \sqrt{2} C_{2} e^{t} \cos (\sqrt{2} t) + \sqrt{2} C_{1} e^{t} \sin (\sqrt{2} t) + \frac{1}{9}$

ySol(t) = simplify(ySol(t))

ySol(t) = 
 $C_{1} e^{t} \cos (\sqrt{2} t) - \frac{t}{3} - C_{2} e^{t} \sin (\sqrt{2} t) - \frac{2}{9}$

由于未指定条件，因此解中出现了常数 C1 和 C2。

在指定初始条件 $u (0) = 2$ 和 $v (0) = - 1$ 的情况下求解该方程组。当以矩阵形式指定方程时，也必须以矩阵形式指定初始条件。dsolve 函数会求出满足这些条件的常数的值。

C = Y(0) == [2;-1];
[xSol(t),ySol(t)] = dsolve(odes,C)

xSol(t) = 
 $\begin{array}{l} \sqrt{2} e^{t} σ_{2} (\frac{17 \sqrt{2}}{18} + \frac{e^{- t} (4 σ_{1} + \sqrt{2} σ_{2} + 6 t σ_{1} + 6 \sqrt{2} t σ_{2})}{18}) - \sqrt{2} e^{t} σ_{1} (\frac{e^{- t} (4 σ_{2} - \sqrt{2} σ_{1} + 6 t σ_{2} - 6 \sqrt{2} t σ_{1})}{18} + \frac{7}{9}) \\ where \\ σ_{1} = \sin (\sqrt{2} t) \\ σ_{2} = \cos (\sqrt{2} t) \end{array}$

ySol(t) = 
 $\begin{array}{l} - e^{t} σ_{1} (\frac{17 \sqrt{2}}{18} + \frac{e^{- t} (4 σ_{1} + \sqrt{2} σ_{2} + 6 t σ_{1} + 6 \sqrt{2} t σ_{2})}{18}) - e^{t} σ_{2} (\frac{e^{- t} (4 σ_{2} - \sqrt{2} σ_{1} + 6 t σ_{2} - 6 \sqrt{2} t σ_{1})}{18} + \frac{7}{9}) \\ where \\ σ_{1} = \sin (\sqrt{2} t) \\ σ_{2} = \cos (\sqrt{2} t) \end{array}$

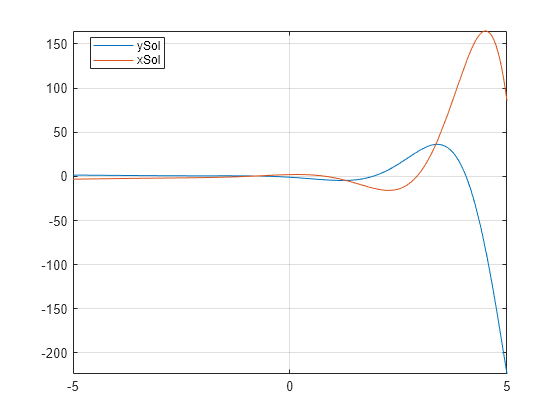
使用 fplot 绘制解的图。

figure
fplot(ySol)
hold on
fplot(xSol)
grid on
legend("ySol","xSol",Location="best")

Figure contains an axes object. The axes object contains 2 objects of type functionline. These objects represent ySol, xSol.

另请参阅

求解微分方程