Solve Equations Numerically
Symbolic Math Toolbox™ offers both numeric and symbolic equation solvers. For a comparison of numeric and symbolic solvers, see Select Numeric or Symbolic Solver. An equation or a system of equations can have multiple solutions. To find these solutions numerically, use the function vpasolve. For polynomial equations, vpasolve returns all solutions. For nonpolynomial equations, vpasolve returns the first solution it finds. These examples show you how to use vpasolve to find solutions to both polynomial and nonpolynomial equations, and how to obtain these solutions to arbitrary precision.
Find All Roots of a Polynomial Function
Use vpasolve to find all the solutions to the function .
syms f(x)
f(x) = 6*x^7-2*x^6+3*x^3-8;
sol = vpasolve(f)sol =
vpasolve returns seven roots of the function, as expected, because the function is a polynomial of degree seven.
Find Zeros of a Nonpolynomial Function Using Search Ranges and Starting Points
A plot of the function reveals periodic zeros, with increasing slopes at the zero points as increases.
syms x h = fplot(exp(x/7)*cos(2*x),[-2 25]); grid on
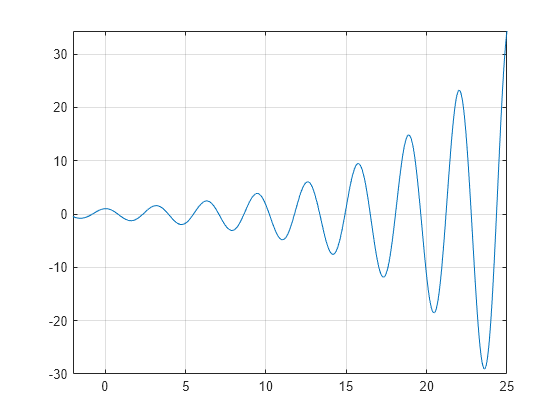
Use vpasolve to find a zero of the function f. Note that vpasolve returns only one solution of a nonpolynomial equation, even if multiple solutions exist. On repeated calls, vpasolve returns the same result.
f = exp(x/7)*cos(2*x); for k = 1:3 vpasolve(f,x) end
ans =
ans =
ans =
To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly. For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.
for k = 1:3 vpasolve(f,x,'Random',true) end
ans =
ans =
ans =
To find a zero close to , set the starting point to 10.
vpasolve(f,x,10)
ans =
To find a zero close to , set the starting point to 1000.
vpasolve(f,x,1000)
ans =
To find a zero in the range , set the search range to [15 25].
vpasolve(f,x,[15 25])
ans =
To find multiple zeros in the range [15 25], you cannot call vpasolve repeatedly because it returns the same result on each call, as previously shown. Instead, set the search range and set 'Random' to true.
for k = 1:3 vpasolve(f,x,[15 25],'Random',true) end
ans =
ans =
ans =
Because 'Random' selects starting points randomly, the same solution might be found on successive calls.
Find All Zeros in a Specified Search Range
Create a function findzeros to systematically find all zeros for f in a given search range, within a specified error tolerance. The function starts with the input search range and calls vpasolve to find a zero. Then, it splits the search range into two around the zero value and recursively calls itself with the new search ranges as inputs to find more zeros.
The function is explained section by section here.
Declare the function with the three inputs and one output. The first input is the function, the second input is the range, and the optional third input allows you to specify the error between a zero and the higher and lower bounds generated from it.
function sol = findzeros(f,range,err)
If you do not specify the optional argument for error tolerance, findzeros sets err to 0.001.
if nargin < 2 err = 1e-3; end
Find a zero in the search range using vpasolve.
sol = vpasolve(f,range);
If vpasolve does not find a zero, exit.
if(isempty(sol)) return
If vpasolve finds a zero, split the search range into two search ranges above and below the zero.
else
lowLimit = sol-err;
highLimit = sol+err;
Call findzeros with the lower search range. If findzeros returns zeros, copy the values into the solution array and sort them.
temp = findzeros(f,[range(1) lowLimit],1); if ~isempty(temp) sol = sort([sol temp]); end
Call findzeros with the higher search range. If findzeros returns zeros, copy the values into the solution array and sort them.
temp = findzeros(f,[highLimit range(2)],1); if ~isempty(temp) sol = sort([sol temp]); end return end end
The entire function findzeros is as follows. Save this function as findzeros.m in the current folder.
function sol = findzeros(f,range,err) if nargin < 3 err = 1e-3; end sol = vpasolve(f,range); if(isempty(sol)) return else lowLimit = sol-err; highLimit = sol+err; temp = findzeros(f,[range(1) lowLimit],1); if ~isempty(temp) sol = sort([sol temp]); end temp = findzeros(f,[highLimit range(2)],1); if ~isempty(temp) sol = sort([sol temp]); end return end end
Call findzeros with search range [15 25] to find all zeros in that range for f(x) = exp(x/7)*cos(2*x), within the default error tolerance.
syms f(x)
f(x) = exp(x/7)*cos(2*x);
sol = findzeros(f,[15 25])'sol =
Obtain Solutions to Arbitrary Precision
Use digits to set the precision of the solutions returned by vpasolve. By default, vpasolve returns solutions to a precision of 32 significant figures.
f = exp(x/7)*cos(2*x); vpasolve(f)
ans =
Use digits to increase the precision to 64 significant figures. When modifying digits, ensure that you save its current value so that you can restore it.
digitsOld = digits; digits(64) vpasolve(f)
ans =
Next, change the precision of the solutions to 16 significant figures.
digits(16)
Solve Multivariate Equations Using Search Ranges
Consider the following system of equations.
A plot of the equations for and shows that the three surfaces intersect in two points. To better visualize the plot, change the line of sight using view.
syms x y z eqn1 = z == 10*(cos(x) + cos(y)); eqn2 = z == x+y^2-0.1*x^2*y; eqn3 = x+y-2.7 == 0; equations = [eqn1 eqn2 eqn3]; fimplicit3(equations) axis([0 2.5 0 2.5 -20 10]) title('System of Multivariate Equations') view(69,28)

Use vpasolve to find a point where the surfaces intersect. The function vpasolve returns a structure. To access the x-, y-, and z-values of the solution, index into the structure.
sol = vpasolve(equations); [sol.x sol.y sol.z]
ans =
To search a region of the solution space, specify search ranges for the variables. If you specify the ranges and , then vpasolve function searches the bounded area shown.

Use vpasolve to find a solution for this search range. To omit a search range for , set the third search range to [NaN NaN].
vars = [x y z]; range = [0 1.5; 1.5 2.5; NaN NaN]; sol = vpasolve(equations,vars,range); [sol.x sol.y sol.z]
ans =
To find multiple solutions, set the 'Random' option to true. This makes vpasolve use random starting points on successive runs. The 'Random' option can be used in conjunction with search ranges to make vpasolve use random starting points within a search range. Because 'Random' selects starting points randomly, the same solution might be found on successive calls. Call vpasolve repeatedly to ensure you find both solutions.
clear sol range = [0 3; 0 3; NaN NaN]; for k = 1:5 temp = vpasolve(equations,vars,range,'Random',true); sol(k,1) = temp.x; sol(k,2) = temp.y; sol(k,3) = temp.z; end sol
sol =
Plot the equations. Superimpose the solutions as a scatter plot of points with yellow X markers using scatter3. To better visualize the plot, make two of the surfaces transparent using alpha and change the line of sight using view.
vpasolve finds solutions at the intersection of the surfaces formed by the equations as shown.
clf ax = axes; h = fimplicit3(equations); h(2).FaceAlpha = 0; h(3).FaceAlpha = 0; axis([0 2.5 0 2.5 -20 10]) hold on scatter3(sol(:,1),sol(:,2),sol(:,3),600,'red','X','LineWidth',2) title('Randomly Found Solutions in Specified Search Range') cz = ax.Children; view(69,28) hold off

Lastly, restore the old value of digits for further calculations.
digits(digitsOld)