ellipticF

Incomplete elliptic integral of the first kind

collapse all in page

Syntax

ellipticF(phi,m)

Description

ellipticF(phi,m) returns the incomplete elliptic integral of the first kind.

example

Examples

Find Incomplete Elliptic Integrals of First Kind

Compute the incomplete elliptic integrals of the first kind for these numbers. Because these numbers are not symbolic objects, you get floating-point results.

s = [ellipticF(pi/3, -10.5), ellipticF(pi/4, -pi),...
 ellipticF(1, -1),  ellipticF(pi/2, 0)]

s =
    0.6184    0.6486    0.8964    1.5708

Compute the incomplete elliptic integrals of the first kind for the same numbers converted to symbolic objects. For most symbolic (exact) numbers, ellipticF returns unresolved symbolic calls.

s = [ellipticF(sym(pi/3), -10.5), ellipticF(sym(pi/4), -pi),...
ellipticF(sym(1), -1),  ellipticF(pi/6, sym(0))]

s =
[ ellipticF(pi/3, -21/2), ellipticF(pi/4, -pi), ellipticF(1, -1), pi/6]

Use vpa to approximate this result with floating-point numbers:

vpa(s, 10)

ans =
[ 0.6184459461, 0.6485970495, 0.8963937895, 0.5235987756]

Differentiate Incomplete Elliptic Integrals of First Kind

Differentiate this expression involving the incomplete elliptic integral of the first kind. ellipticE represents the incomplete elliptic integral of the second kind.

syms m
diff(ellipticF(pi/4, m))

ans =
1/(4*(1 - m/2)^(1/2)*(m - 1)) - ellipticF(pi/4, m)/(2*m) -...
ellipticE(pi/4, m)/(2*m*(m - 1))

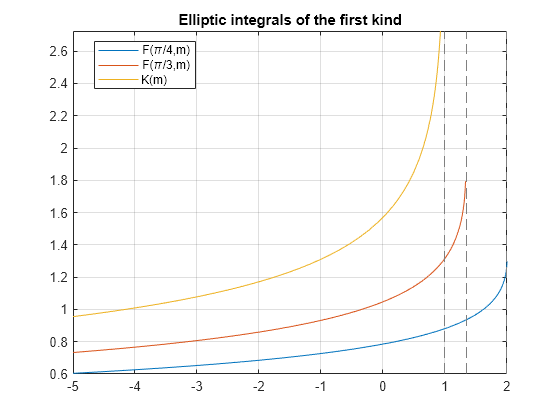
Plot Incomplete and Complete Elliptic Integrals

Plot the incomplete elliptic integrals ellipticF(phi,m) for phi = pi/4 and phi = pi/3. Also plot the complete elliptic integral ellipticK(m).

syms m
fplot([ellipticF(pi/4, m) ellipticF(pi/3, m) ellipticK(m)])
grid on

title('Elliptic integrals of the first kind')
legend('F(\pi/4,m)', 'F(\pi/3,m)', 'K(m)', 'Location', 'Best')

$Figure contains an axes object. The axes object with title Elliptic integrals of the first kind contains 3 objects of type functionline. These objects represent F(\pi/4,m), F(\pi/3,m), K(m).$

Input Arguments

collapse all

`m` — Input
number | vector | matrix | array | symbolic number | symbolic variable | symbolic array | symbolic function | symbolic expression

Input, specified as a number, vector, matrix, or array, or a symbolic number, variable, array, function, or expression.

`phi` — Input
number | vector | matrix | array | symbolic number | symbolic variable | symbolic array | symbolic function | symbolic expression

Input, specified as a number, vector, matrix, or array, or a symbolic number, variable, array, function, or expression.

More About

collapse all

Incomplete Elliptic Integral of the First Kind

The complete elliptic integral of the first kind is defined as follows:

$F (φ | m) = \int_{0}^{φ} \frac{1}{\sqrt{1 - m \sin^{2} θ}} d θ$

Note that some definitions use the elliptical modulus k or the modular angle α instead of the parameter m. They are related as m = k² = sin²α.

Tips

ellipticF returns floating-point results for numeric arguments that are not symbolic objects.
For most symbolic (exact) numbers, ellipticF returns unresolved symbolic calls. You can approximate such results with floating-point numbers using vpa.
At least one input argument must be a scalar or both arguments must be vectors or matrices of the same size. If one input argument is a scalar and the other one is a vector or a matrix, ellipticF expands the scalar into a vector or matrix of the same size as the other argument with all elements equal to that scalar.
ellipticF(pi/2, m) = ellipticK(m).

References

[1] Milne-Thomson, L. M. “Elliptic Integrals.” Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. (M. Abramowitz and I. A. Stegun, eds.). New York: Dover, 1972.

Version History

Introduced in R2013a