Main Content

ellipticNome

Elliptic nome function

collapse all in page

Syntax

ellipticNome(m)

Description

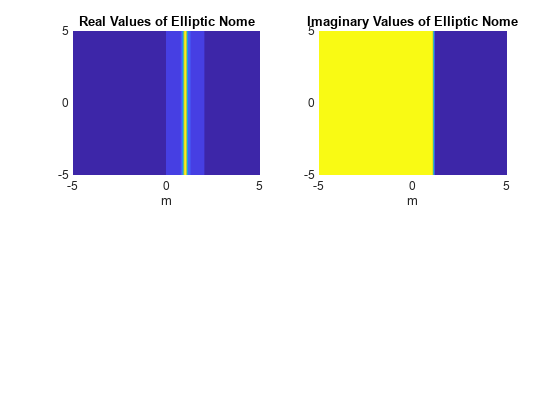
ellipticNome(m) returns the Elliptic Nome of m. If m is an array, then ellipticNome acts element-wise.

example

Examples

collapse all

ellipticNome(1.3)
ans =
   0.0881 - 0.2012i

Call ellipticNome on array inputs. ellipticNome acts element-wise when m is an array.

ellipticNome([2 1 -3/2])
ans =
   0.0000 - 0.2079i   1.0000 + 0.0000i  -0.0570 + 0.0000i

Convert numeric input to symbolic form using sym, and find the elliptic nome. For symbolic input where m = 0, 1/2, or 1, ellipticNome returns exact symbolic output.

ellipticNome([0 1/2 1])
ans =
         0    0.0432    1.0000

Show that for any other symbolic values of m, ellipticNome returns an unevaluated function call.

ellipticNome(sym(2))
ans =
ellipticNome(2)

For symbolic variables or expressions, ellipticNome returns the unevaluated function call.

syms x
f = ellipticNome(x)
f =
ellipticNome(x)

Substitute values for the variables by using subs, and convert values to double by using double.

f = subs(f, x, 5)
f =
ellipticNome(5)
fVal = double(f)
fVal =
  -0.1008 - 0.1992i

Calculate f to higher precision using vpa.

fVal = vpa(f)
fVal =
- 0.10080189716733475056506021415746 - 0.19922973618609837873340100821425i
Open Live Script

Plot the real and imaginary values of the elliptic nome using fcontour. Fill plot contours by setting Fill to on.

syms m
f = ellipticNome(m);

subplot(2,2,1)
fcontour(real(f),'Fill','on')
title('Real Values of Elliptic Nome')
xlabel('m')

subplot(2,2,2)
fcontour(imag(f),'Fill','on')
title('Imaginary Values of Elliptic Nome')
xlabel('m')

Figure contains 2 axes objects. Axes object 1 with title Real Values of Elliptic Nome, xlabel m contains an object of type functioncontour. Axes object 2 with title Imaginary Values of Elliptic Nome, xlabel m contains an object of type functioncontour.

Input Arguments

collapse all

Input, specified as a number, vector, matrix, or multidimensional array, or a symbolic number, variable, vector, matrix, multidimensional array, function, or expression.

More About

collapse all

Elliptic Nome

The elliptic nome is

q(m)=e−πK′(m)K(m)

where K is the complete elliptic integral of the first kind, implemented as ellipticK.

|q(m)|≤1 holds for all m∈ℂ.

Version History

Introduced in R2017b

See Also

| | | | | | | | | | | | |