zeta
Riemann zeta function
Description
Examples
Find Riemann Zeta Function for Numeric and Symbolic Inputs
Find the Riemann zeta function for numeric inputs.
zeta([0.7 i 4 11/3])
ans = -2.7784 + 0.0000i 0.0033 - 0.4182i 1.0823 + 0.0000i 1.1094 + 0.0000i
Find the Riemann zeta function symbolically by converting the inputs to symbolic objects
using sym. The zeta function returns exact
results.
zeta(sym([0.7 i 4 11/3]))
ans = [ zeta(7/10), zeta(1i), pi^4/90, zeta(11/3)]
zeta returns unevaluated function calls for symbolic inputs that do
not have results implemented. The implemented results are listed in Algorithms.
Find the Riemann zeta function for a matrix of symbolic expressions.
syms x y Z = zeta([x sin(x); 8*x/11 x + y])
Z = [ zeta(x), zeta(sin(x))] [ zeta((8*x)/11), zeta(x + y)]
Find Riemann Zeta Function for Large Inputs
For values of |z|>1000,
zeta(z) might return an unevaluated function call. Use
expand to force zeta to evaluate the function
call.
zeta(sym(1002)) expand(zeta(sym(1002)))
ans = zeta(1002) ans = (1087503...312*pi^1002)/15156647...375
Differentiate Riemann Zeta Function
Find the third derivative of the Riemann zeta function at point
x.
syms x expr = zeta(3,x)
expr = zeta(3, x)
Find the third derivative at x = 4 by substituting
4 for x using subs.
expr = subs(expr,x,4)
expr = zeta(3, 4)
Evaluate expr using vpa.
expr = vpa(expr)
expr = -0.07264084989132137196244616781177
Plot Zeros of Riemann Zeta Function
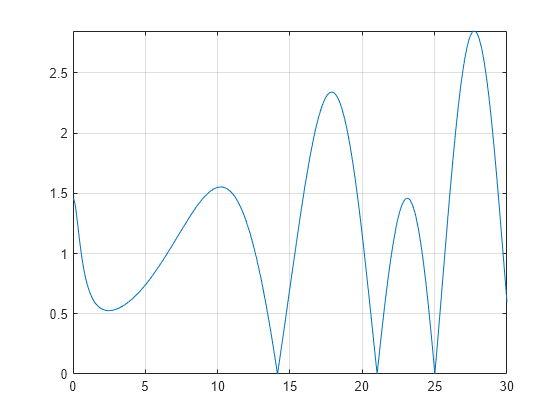
Zeros of the Riemann Zeta function zeta(x+i*y) are found along the line x = 1/2. Plot the absolute value of the function along this line for 0<y<30 to view the first three zeros.
syms y fplot(abs(zeta(1/2+1i*y)),[0 30]) grid on
Input Arguments
More About
Tips
Floating point evaluation is slow for large values of
n.
Algorithms
The following exact values are implemented.
If and
zis an even integer,If and
zis an odd integerFor ,
zeta(z)returns an unevaluated function call. To force evaluation, useexpand(zeta(z)).If and
zis an even integerFor ,
zeta(z)returns an unevaluated function call. To force evaluation, useexpand(zeta(z)).If ,
If the argument does not evaluate to a listed special value,
zetareturns the symbolic function call.
Version History
Introduced before R2006a
See Also
bernoulli | hurwitzZeta | gamma | psi