使用 ThingSpeak 数据预测潮汐深度
此示例显示如何使用存储在 ThingSpeak™ 通道中的数据预测 Ockway Bay 的潮汐深度。预测潮汐深度至关重要:如果您不知道水深,您的船很容易被困在浅海湾的泥里。
从 Ockway Bay 实时潮汐仪读取数据
ThingSpeak™ 通道 50289 包含有关奥克威湾潮汐深度的数据。每 5 分钟收集一次数据。该通道的字段 1 包含潮汐深度数据。使用 thingSpeakRead 函数从通道 50289 读取某一天的数据,例如 2016 年 7 月 1 日。
startDate = datetime('July 1, 2016 12:01:00 AM'); endDate = datetime('July 2, 2016 12:02:00 AM'); dateRange = startDate:endDate; data = thingSpeakRead(50289,'DateRange',dateRange,'Fields',1);
用 AR 模型拟合数据
使用 iddata 函数创建潮汐深度数据的 iddata 对象。对数据使用 detrend 使数据为零均值。由于潮汐深度随时间变化,使用 ar 函数将离散时间自回归模型拟合到数据。捕获去趋势之前的偏移,然后拟合 AR 模型来表示系统。
sampleTime = 5; IDdata = iddata(data,[],sampleTime,'OutputName',{'Tidal Depth'},'TimeUnit','minutes') trend = getTrend(IDdata,0); IDdata = detrend(IDdata,0); modelOrder = 8; sys = ar(IDdata,modelOrder);
IDdata =
Time domain data set with 288 samples.
Sample time: 5 minutes
Outputs Unit (if specified)
Tidal Depth
预测潮汐深度
使用 forecast 函数预测第二天的潮汐深度。由于测量的潮汐深度数据每 5 分钟更新一次,因此将预测数据的样本数设置为 288。yf 是预测的模型响应,yf_sd 是输出的标准偏差。绘图之前重新趋势数据。
numSamples = 288; [yf,x0,sysf,yf_sd,x,x_sd] = forecast(sys,IDdata,numSamples); IDdata = retrend(IDdata,trend); yf = retrend(yf,trend);
绘制预测响应
将测量数据与预测的潮汐数据绘制成图。还绘制了预测模型不确定性的一个标准差。
figure; UpperBound = iddata(yf.OutputData+1*yf_sd,[],yf.Ts,'Tstart',yf.Tstart,'TimeUnit','minutes'); LowerBound = iddata(yf.OutputData-1*yf_sd,[],yf.Ts,'Tstart',yf.Tstart,'TimeUnit','minutes'); plot(IDdata(:,:,[]),'r',yf(:,:,[]),'b'); hold on plot(UpperBound,'k--',LowerBound,'k--'); legend({'measured','forecasted','1 sd uncertainty'},'Location','best'); xlabel('Time'); ylabel('Tidal depth (inches)'); title('Measured and Forecasted Tidal Wave Depths');
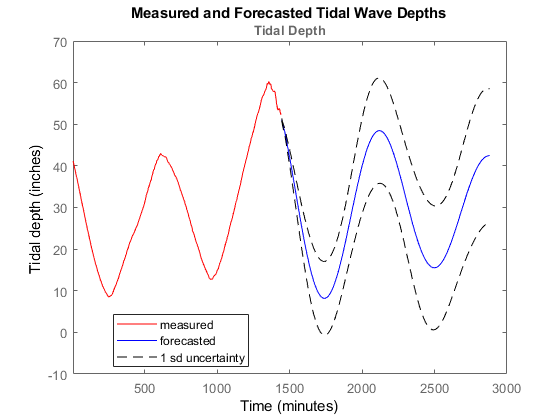
该图显示了测量和预测的系统响应以及一个标准差不确定性界限。