Contrast Limited Adaptive Histogram Equalization
This example shows how to implement a contrast-limited adaptive histogram equalization (CLAHE) algorithm using Simulink® blocks. The example model is FPGA-hardware compatible.
The example uses the adapthisteq function from the Image Processing Toolbox™ as reference to verify the design.
Introduction
Adaptive histogram equalization (AHE) is an image pre-processing technique used to improve contrast in images. It computes several histograms, each corresponding to a distinct section of the image, and uses them to redistribute the luminance values of the image. It is therefore suitable for improving the local contrast and enhancing the definitions of edges in each region of an image. However, AHE has a tendency to overamplify noise in relatively homogeneous regions of an image. A variant of adaptive histogram equalization called contrast-limited adaptive histogram equalization (CLAHE) prevents this effect by limiting the amplification.
CLAHE Algorithm
The CLAHE algorithm has three major parts: tile generation, histogram equalization, and bilinear interpolation. The input image is first divided into sections. Each section is called a tile. The input image shown in the figure is divided into four tiles. Histogram equalization is then performed on each tile using a pre-defined clip limit. Histogram equalization consists of five steps: histogram computation, excess calculation, excess distribution, excess redistribution, and scaling and mapping using a cumulative distribution function (CDF). The histogram is computed as a set of bins for each tile. Histogram bin values higher than the clip limit are accumulated and distributed into other bins. CDF is then calculated for the histogram values. CDF values of each tile are scaled and mapped using the input image pixel values. The resulting tiles are stitched together using bilinear interpolation, to generate an output image with improved contrast.
HDL Implementation
This figure shows the block diagram of the HDL implementation of the CLAHE algorithm. It consists of a tile generation block, a histogram equalization pipeline block, a bilinear interpolation block, and an input image buffer block. Tiles are generated by modifying the pixelcontrol bus of the pixel stream for the desired tile size. The pixel stream and the modified pixelcontrol bus are fed to the histogram equalization pipeline. Two histogram equalization pipelines are required to keep pace with the input data. They operate in ping-pong manner. Each pipeline contains histogram equalization modules equal to the number of tiles in the horizontal direction. The histogram equalization modules work in parallel to compute histogram equalization for each tile. The last stage in the histogram equalization module, scaling and mapping, needs the original input image data. This data is stored in an input image buffer block. The bilinear interpolation block generates addresses to read the input image pixel values from the memory. The input image pixel values from the image buffer block are given to the histogram equalization modules for mapping. Mapped values obtained from histogram equalization are scaled and used in the bilinear interpolation computation to reduce boundary artifacts.
modelname = 'CLAHEExample'; open_system(modelname,'force'); set_param(modelname,'SampleTimeColors','off'); set_param(modelname,'Open','on'); set_param(modelname,'SimulationCommand','Update'); set(allchild(0),'Visible','off');

The figure shows the top level view of the CLAHEExample model. The input image path is specified in the inputImage block. The input image frame is converted to a pixel stream and pixelcontrol bus using a Frame To Pixels block. The pixel stream is passed to the CLAHEHDLAlgorithm subsystem for contrast enhancement and is also stored in the imgBuffer subsystem. While processing, the CLAHEHDLAlgorithm subsystem generates the address to read image data from the imgBuffer subsystem. The pixel value read from the imgBuffer subsystem is passed to CLAHEHDLAlgorithm for adjustment. The adjusted pixel values are given to the Pixels To Frame block and converted to a frame using the control signals. The Result subsystem shows the input image and output image once all the pixels in the frame have been received by the Pixels To Frame block.
Tile Generation
system = 'CLAHEExample/CLAHEHDLAlgorithm/tileGeneration'; open_system(system,'force');
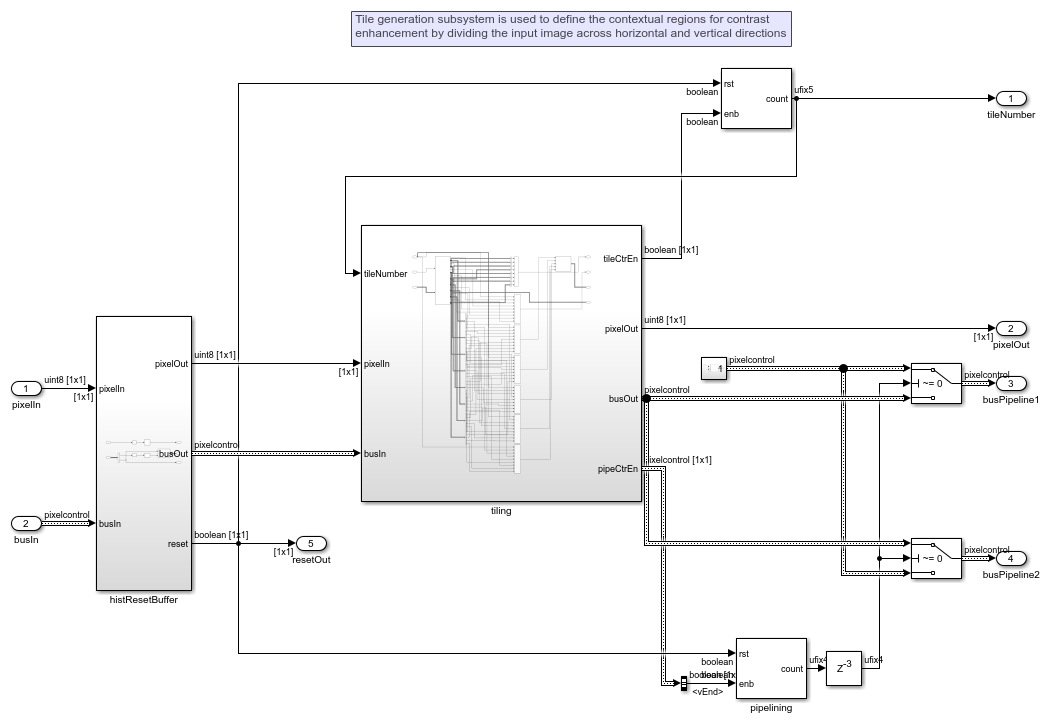
The figure shows the tile generation subsystem. This subsystem is used to divide the input image into a number of tiles in both the horizontal and vertical directions. By default, the model divides the input image into 8 tiles in each direction. Tiles are created by modifying the input pixelcontrol bus to select the pixels in each tile region. The size of a vertical(horizontal) tile is computed by dividing the number of rows(columns) in the input image by the number of tiles in the same direction. Inside the tiling subsystem, the ROI Selector block has vertical reuse enabled. This option enables parallel processing of the vertical tiles and the RoI Selector generates pixel streams and corresponding pixelcontrol buses for each of the horizontal tiles. The pixel stream to the histogram equalization pipeline is controlled by diverting each vertical tile to an alternate pipe. The tile size calculated in either must be an even integer. If the input image does not divide into an integer number of even-sized tiles, pad the input image symmetrically.
Histogram Equalization Pipeline
system = 'CLAHEExample/CLAHEHDLAlgorithm/histoEqPipeline/'; subsystem = [system 'histPipe1']; open_system(subsystem,'force');

Two histogram equalization pipelines are used to keep pace with the streaming input pixels. Each histogram equalization pipeline consists of histogram equalization modules corresponding to each tile in the horizontal direction. These modules are implemented by using a For Each subsystem. Each histogram equalization module is divided into five stages: histogram calculation, total excess calculation, total excess distribution, excess redistribution, cumulative distribution function, and mapping.
The first module of the histogram pipeline, histoExcess subsystem, performs histogram calculation and total excess calculation for each tile. To compute the histogram, the Histogram block is used. When the histogram is complete the block generates a readRdy signal. The subsystem then reads the histogram values and determines excess value from each bin by using clip limit value. The clip limit is computed from the normalized clip limit value specified using these equations.
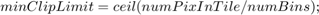

The excess value from each bin is accumulated to form total excess value. The previously computed histogram values are not changed during total excess calculation and are stored in a Simple Dual Port RAM memory block. The necessary control signals for the RAM block (ramBus) are generated by the histoExcess subsystem. The total excess value calculated in the histoExcess subsystem is used by the Distribute subsystem.
The Distribute subsystem computes two variables: average bin increment and upper limit. These values are computed from the total excess value by using these equations:
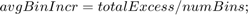
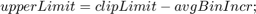
The Distribute subsystem then reads the value of each histogram bin from the RAM block. It updates the value at every bin based on these three conditions:
If the histogram value of a bin is greater than the clip limit, it is replaced with the clip limit.
If the histogram value of a bin is between the clip limit and the upper limit, the histogram value is replaced with the clip limit. The total excess value is reduced by the number of added pixels equal to
(clipLimit - histVal).If the histogram value of a bin is less than the upper limit, the histogram value is increased by the average bin increment. The total excess value is reduced by the average bin increment.
The adjusted histogram value is stored at the same address. The remaining total excess value is passed to the Redistribute subsystem as excess value.
system = 'CLAHEExample/CLAHEHDLAlgorithm/histoEqPipeline/'; subsystem = [system 'histPipe1/redistribute']; open_system(subsystem,'force');
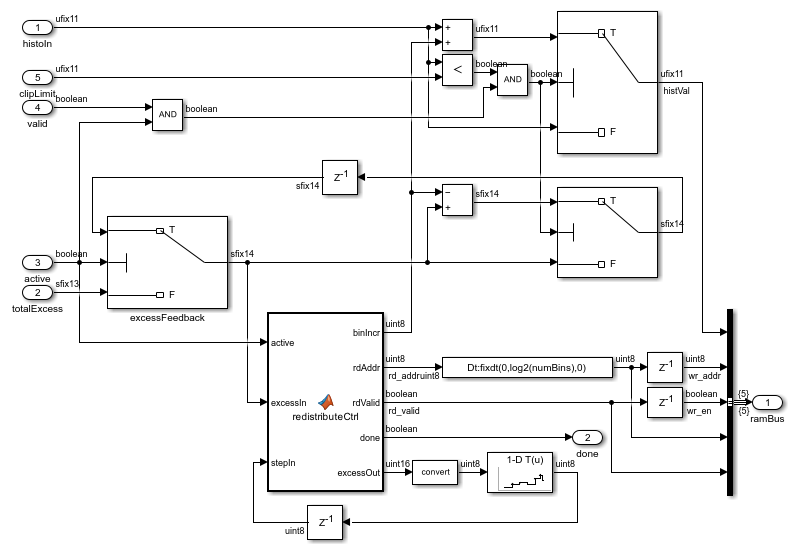
The Redistribute subsystem distributes spillover excess values to the histogram bins. It primarily uses two variables to distribute excess values: binIncr and step. binIncr specifies the value to be added to the histogram bins. step specifies the increment in the address counter used to fetch the histogram bin value. If the excess is greater than or equal to the number of bins, then binIncr is calculated by dividing the excess value by the number of bins, and step is set to 1. The divide is implemented by using a right-shift operation, since the number of bins is a power of 2.
If the excess is less than the number of bins, binIncr is set to 1 and step is calculated by dividing the number of bins by the excess value. The divide is computed by using a n-D Lookup Table (Simulink) block. The redistributeCtrl MATLAB Function generates the address for the RAM block by using the step value computed. When the address reaches the total number of bins, the step value is re-computed using the most recent excess value. Care is taken to not repeat the first bin as the start bin for redistribution. If the value of the histogram bin is less than the clip limit, it is increased by binIncr, and the same value is subtracted from the excess value. If the value of histogram bin is equal to the clip limit, no operation is performed and the value is written back to the same address. The MATLAB Function block repeats these bin adjustments until the excess value reaches 0.
The last stage of the histogram equalization pipeline is CDF calculation. The CDF subsystem computes the cumulative sum of the histogram bin values. The histogram values are read from the RAM block and added to the sum of the previous histogram bin values. It is then stored to the same address.
The five stages of the histogram equalization module can be considered as five states. The five states of histogram equalization module are sequential. Thus, a state counter is used to move from one state to another state. A counter value determines the state of the histogram equalization module. A Multiport Switch (Simulink) block is used with the state counter as the index value. The multi-port switch connects the ramBus from each state with the correct memory according to the index. The state counter is in state 1 in idle condition. When histoExcess finishes excess calculation it sets the done signal to 1 for one cycle, and the state counter moves to state 2. Similarly, the distribute subsystem, redistribute subsystem, and cdf subsystem generate done flags when their processing completes. These done flags increment the state counter to state 5, where it uses input image pixel values from the input image buffer block as addresses to read CDF values from the RAM. Before being used as address, the input image pixel values are scaled according to the number of histogram bins. When the number of histogram bins are less than the number of input image intensity levels, the latter values are mapped to the same range as CDF values. The address counter that reads the input image values is driven by the bilinear interpolation subsystem. The state counter is incremented by the bilinear interpolation subsystem when mapping for the respective pipeline is complete.
Bilinear Interpolation
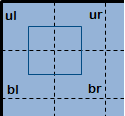
Bilinear interpolation is used to smooth edges when the tiles are stitched together. The figure shows how four tiles are used to compute pixel values in the output image. The each tile is divided into four parts. One part from each of the four tiles are grouped together to compute bilinear interpolation for that section of the image.
Interpolation uses this equation:

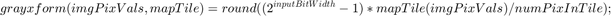
The bilinear interpolation equation uses the position of a pixel with respect to each tile and the intensity information at that position to compute a pixel value in the output image. The intensity information is obtained from the input image pixel values stored in the image buffer. For corner tiles, intensity values are replicated (mirrored). The intensity information at the respective position in each tile is extracted from the CDF function of the histogram equalization pipeline by using the input image pixel value at the same position. The grayxform function scales the values obtained from the CDF function. The result is then divided by the number of pixels in a tile, represented as normFactor in the equation.
system = 'CLAHEExample/CLAHEHDLAlgorithm/bilinearInterpolation'; open_system(system,'force');
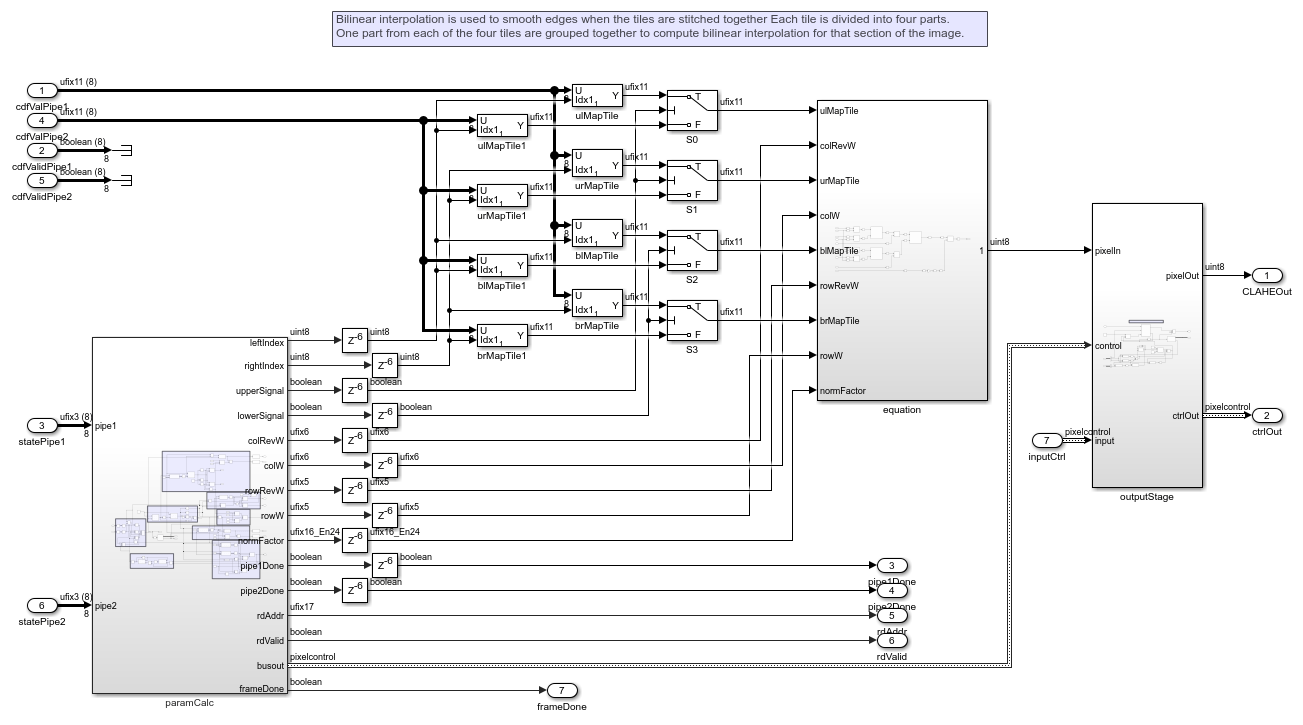
The figure shows the HDL implementation of the bilinear interpolation subsystem. When the histogram equalization pipeline reaches state 5, the paramCalc subsystem starts computing the read address for the imgBuffer subsystem. The pixel value read from the buffered image is the address for the RAM in the histogram equalization pipeline. CDF values are fetched from the read address for all the tiles from both the histogram equalization pipelines simultaneously. The required CDF values are selected and passed to the equation subsystem using Selector Switch blocks and Switch blocks. The Switch block selects which pipeline contains upper/lower tiles and the Selector Switch blocks select data corresponding to left/right tiles. The control signals for the Selector Switch and Switch blocks are generated in the paramCalc subsystem by using a read counter. Thus, intensity values at a pixel position for each tile are obtained from the image buffer. The bilinear interpolation equation also requires the pixel position and the total number of pixels in the tile. These parameters are also generated in the paramCalc subsystem. The equation subsystem is pipelined to optimize performance in hardware. The result is returned as a pixel stream with a pixelcontrol bus.
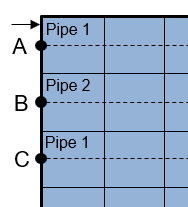
Bilinear interpolation of the output image is computed by traversing the rows from left to right. When all histogram equalization modules in the first pipeline have reached state 5, the paramCalc subsystem is enabled. The read addresses for the imgBuffer subsystem are computed until point A. Further computation of bilinear interpolation requires values from the histogram equalization modules of the second pipeline. When all histogram equalization modules in the second pipeline have reached state 5, the read address counter is again enabled and the bilinear interpolation output results are computed for pixel positions between point A and point B. Once the address counter reaches point B, results from first pipeline are no longer required. The pipe1Done signal is generated to change the state of the first histogram equalization pipeline modules back to state 1. Until this point, the tiles in the first pipeline are upper tiles and the tiles in the second pipeline are lower tiles. For the computation of values between point B and point C, the tiles in the second pipeline become the upper tiles and tiles in the first pipeline are now lower tiles. This operation continues until only the lowest tiles in the image remain. The output for these tiles is computed by replicating the values for the other pipeline. The output results are pushed into a FIFO in the outputStage subsystem and popped out such that the output valid signal is similar to that of the input pixel stream.
Model Parameters
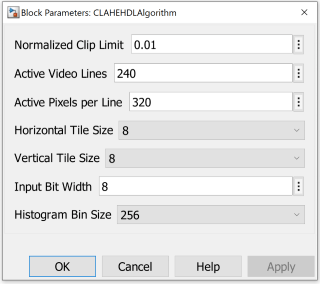
CLAHE uses a clip limit to prevent over-saturation of the image in homogeneous areas. These areas are characterized by a high peak in the histogram of an image tile due to many pixels falling in the same intensity range. For the model presented here, the clip limit is a user-defined normalized value. The default value is 0.01 (as shown in figure). The clip limit can be any value between 0 and 1 (inclusive).
The input image frame dimensions are specified by Active Video Lines and Active Pixels Per Line. The input image frame size is essential in setting the tile dimensions. Tiles define the number of rectangular contextual regions into which the image is divided. The horizontal and vertical tile size refer to the number of tiles in the relevant direction. Both these values must be at least 2 and the input image can only be divided into an integer number of even-sized tiles. The tile size mask parameters are automatically populated with the valid options for each image dimension. The optimal number of tiles depends on the type of the input image, and it is best determined through experimentation.
The input bit width defines the number of bits per pixel in the input image. This helps to determine the maximum intensity value the input image can represent. The number of histogram bins used to build the contrast enhancing transformation can be varied from 32 to 4096. If the image dimensions or tile sizes are too small, higher bin sizes are not architecturally supported and the valid options are automatically populated. Higher values of histogram bins result in greater dynamic range, hence a better resolution at the cost of higher design latency.
Simulation and Results
This example uses an input image of size 240-by-320 pixels, whose path is specified in the inputImage block. The input image pixels are specified by an input bit width of 8 equivalent to uint8 data type. For 8 tiles in each direction, the computed tile size is 30-by-40 and the number of pixels in each tile is 1200. The number of histogram bins is set to 256.
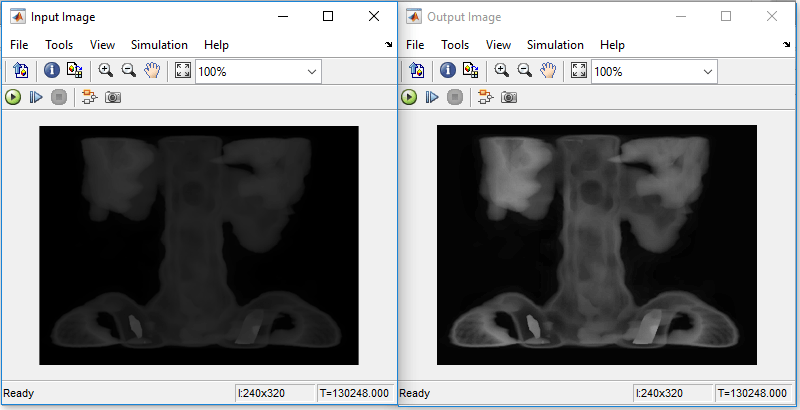
This figure shows the input image and output image from the CLAHE model. The result shows the improved contrast in the output image, without over- saturation. The result of the CLAHE HDL model matches the adaphisteq function in MATLAB and has an error of only a few pixels.
HDL code can be generated for the CLAHEHDL subsystem. An HDL Coder™ license is required to generate HDL code. This design was synthesized on the Intel® Arria® 10 GX platform, for 10AX115S2F45I1SG FPGA device. The table shows the resource utilization. The HDL design achieves a clock rate of over 200 MHz.
% ================================================ % |Model Name || CLAHEHDL || % ================================================ % |Input Image Resolution || 320 x 240 || % |ALM Utilization || 48045 || % |Total Registers || 51688 || % |Total RAM Blocks || 63 || % |Total DSP Blocks || 6 || % ================================================
References
Karel Zuiderveld, "Contrast Limited Adaptive Histogram Equalization", Graphics Gems IV, p. 474-485, code: p. 479-484.