Main Content

idwt

Single-level 1-D inverse discrete wavelet transform

collapse all in page

    Syntax

    x = idwt(cA,cD,wname)
    x = idwt(cA,cD,LoR,HiR)
    x = idwt(___,l)
    x = idwt(___,'mode',mode)
    x = idwt(cA,[],___)
    x = idwt([],cD,___)

    Description

    x = idwt(cA,cD,wname) returns the single-level one-dimensional wavelet reconstruction x based on the approximation and detail coefficients cA and cD, respectively, using the wavelet specified by wname. For more information, see dwt.

    Let la be the length of cA (which also equals the length of cD), and lf the length of the reconstruction filters associated with wname (see wfilters). If the DWT extension mode is set to periodization, then the length of x is equal to 2la. Otherwise, the length of x is equal to 2la- 2lf+2. For more information, see dwtmode.

    example

    x = idwt(cA,cD,LoR,HiR) uses the specified lowpass and highpass wavelet reconstruction filters LoR and HiR, respectively.

    example

    x = idwt(___,l) returns the length-l central portion of the reconstruction. This argument can be added to any of the previous input syntaxes

    x = idwt(___,'mode',mode) uses the specified DWT extension mode mode. For more information, see dwtmode. This argument can be added to any of the previous syntaxes.

    x = idwt(cA,[],___) returns the single-level reconstructed approximation coefficients based on the approximation coefficients cA.

    x = idwt([],cD,___) returns the single-level reconstructed detail coefficients based on the detail coefficients cD.

    Examples

    collapse all

    Open Live Script

    Demonstrate perfect reconstruction using dwt and idwt with an orthonormal wavelet. 

    load noisdopp;
[A,D] = dwt(noisdopp,'sym4');
x = idwt(A,D,'sym4');
max(abs(noisdopp-x))
    ans = 
3.2152e-12
    Open Live Script

    Demonstrate perfect reconstruction using dwt and idwt with a biorthogonal wavelet. 

    load noisdopp;
[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('bior3.5');
[A,D] = dwt(noisdopp,Lo_D,Hi_D);
x = idwt(A,D,Lo_R,Hi_R);
max(abs(noisdopp-x))
    ans = 
2.6645e-15

    Input Arguments

    collapse all

    Approximation coefficients, specified as a vector. cA is expected to be the output of dwt.

    Data Types: single | double
    Complex Number Support: Yes

    Detail coefficients, specified as a vector. cD is expected to be the output of dwt.

    Data Types: single | double
    Complex Number Support: Yes

    Wavelet used to compute the single-level inverse discrete wavelet transform (IDWT), specified as a character vector or string scalar. The wavelet must be recognized by wavemngr. The wavelet is from one of the following wavelet families: Best-localized Daubechies, Beylkin, Coiflets, Daubechies, Fejér-Korovkin, Haar, Han linear-phase moments, Morris minimum-bandwidth, Symlets, Vaidyanathan, Discrete Meyer, Biorthogonal, and Reverse Biorthogonal. See wfilters for the wavelets available in each family.

    The wavelet specified must be the same wavelet used to obtain the approximation and detail coefficients.

    Example: 'db4'

    Wavelet reconstruction filters, specified as a pair of even-length real-valued vectors. LoR is the lowpass reconstruction filter, and HiR is the highpass reconstruction filter. The lengths of LoR and HiR must be equal. See wfilters for additional information.

    Data Types: single | double

    Length of central portion of reconstruction, specified as a positive integer. If xrec = idwt(cA,cD,wname), then l cannot exceed length(xrec).

    Data Types: single | double

    DWT extension mode used in the wavelet reconstruction, specified as a character vector or string scalar. For possible extension modes, see dwtmode.

    Algorithms

    Starting from the approximation and detail coefficients at level j, cAj and cDj, the inverse discrete wavelet transform reconstructs cAj−1, inverting the decomposition step by inserting zeros and convolving the results with the reconstruction filters.

    where

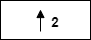    • — Insert zeros at even-indexed elements

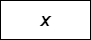    • — Convolve with filter X

    • — Take the central part of U with the convenient length

    References

    [1] Daubechies, I. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics. Philadelphia, PA: Society for Industrial and Applied Mathematics, 1992.

    [2] Mallat, S. G. “A Theory for Multiresolution Signal Decomposition: The Wavelet Representation.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 11, Issue 7, July 1989, pp. 674–693.

    [3] Meyer, Y. Wavelets and Operators. Translated by D. H. Salinger. Cambridge, UK: Cambridge University Press, 1995.

    Extended Capabilities

    Version History

    Introduced before R2006a

    See Also

    | |