dwt

Single-level 1-D discrete wavelet transform

Syntax

[cA,cD] = dwt(x,wname)

[cA,cD] = dwt(x,LoD,HiD)

[cA,cD] = dwt(___,'mode',extmode)

Description

[cA,cD] = dwt(x,wname) returns the single-level discrete wavelet transform (DWT) of the vector x using the wavelet specified by wname. The wavelet must be recognized by wavemngr. dwt returns the approximation coefficients vector cA and detail coefficients vector cD of the DWT.

Note

If your application requires a multilevel wavelet decomposition, consider using wavedec.

example

[cA,cD] = dwt(x,LoD,HiD) returns the single-level DWT using the specified lowpass and highpass wavelet decomposition filters LoD and HiD, respectively.

example

[cA,cD] = dwt(___,'mode',extmode) returns the single-level DWT with the specified extension mode extmode. For more information, see dwtmode. This argument can be added to any of the previous input syntaxes.

Note

For gpuArray inputs, the supported modes are 'symh' ('sym') and 'per'. All 'mode' options except 'per' are converted to 'symh'. See the example Single-Level Discrete Wavelet Transform on a GPU.

Examples

collapse all

DWT Using Wavelet Name

Open Live Script

Obtain the single-level DWT of the noisy Doppler signal using a wavelet name.

load noisdopp;
[cA,cD] = dwt(noisdopp,'sym4');

Reconstruct a smoothed version of the signal using the approximation coefficients. Plot and compare with the original signal.

xrec = idwt(cA,zeros(size(cA)),'sym4');
plot(noisdopp)
hold on
grid on
plot(xrec)
legend('Original','Reconstruction')

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Original, Reconstruction.

DWT Using Wavelet and Scaling Filters

Open Live Script

Obtain the single-level DWT of a noisy Doppler signal using the wavelet (highpass) and scaling (lowpass) filters.

load noisdopp;
[LoD,HiD] = wfilters('bior3.5','d');
[cA,cD] = dwt(noisdopp,LoD,HiD);

Create a DWT filter bank that can be applied to the noisy Doppler signal using the same wavelet. Obtain the highpass and lowpass filters from the filter bank.

len = length(noisdopp);
fb = dwtfilterbank('SignalLength',len,'Wavelet','bior3.5');
[lo,hi] = filters(fb);

For the bior3.5 wavelet, lo and hi are 12-by-2 matrices. lo are the lowpass filters, and hi are the highpass filters. The first columns of lo and hi are used for analysis and the second columns are used for synthesis. Compare the first column of lo and hi with LoD and HiD respectively. Confirm they are equal.

disp('Lowpass Analysis Filters')

Lowpass Analysis Filters

[lo(:,1) LoD']

ans = 12×2

   -0.0138   -0.0138
    0.0414    0.0414
    0.0525    0.0525
   -0.2679   -0.2679
   -0.0718   -0.0718
    0.9667    0.9667
    0.9667    0.9667
   -0.0718   -0.0718
   -0.2679   -0.2679
    0.0525    0.0525
      ⋮

disp('Highpass Analysis Filters')

Highpass Analysis Filters

[hi(:,1) HiD']

ans = 12×2

         0         0
         0         0
         0         0
         0         0
   -0.1768   -0.1768
    0.5303    0.5303
   -0.5303   -0.5303
    0.1768    0.1768
         0         0
         0         0
      ⋮

Plot the one-sided magnitude frequency responses of the first-level wavelet and scaling filters.

[psidft,f,phidft] = freqz(fb);
level = 1;
plot(f(len/2+1:end),abs(phidft(level,len/2+1:end)))
hold on
plot(f(len/2+1:end),abs(psidft(level,len/2+1:end)))
grid on
legend('Scaling Filter','Wavelet Filter')
title('First-Level One-sided Frequency Responses')
xlabel('Normalized Frequency (cycles/sample)')
ylabel('Magnitude')

Figure contains an axes object. The axes object with title First-Level One-sided Frequency Responses, xlabel Normalized Frequency (cycles/sample), ylabel Magnitude contains 2 objects of type line. These objects represent Scaling Filter, Wavelet Filter.

Single-Level Discrete Wavelet Transform on a GPU

This example uses:

Open Live Script

Refer to GPU Computing Requirements (Parallel Computing Toolbox) to see what GPUs are supported.

Load the noisy Doppler signal. Put the signal on the GPU using gpuArray. Save the current extension mode.

load noisdopp
noisdoppg = gpuArray(noisdopp);
origMode = dwtmode('status','nodisp');

Use dwtmode to change the extension mode to zero-padding. Obtain the single-level discrete wavelet transform of the signal on the GPU using the db2 wavelet.

dwtmode('zpd','nodisp')
[cA,cD] = dwt(noisdoppg,'db2');

The current extension mode zpd is not supported for gpuArray input. Therefore, the DWT is instead performed using the sym extension mode. Confirm this by taking the DWT of noisdoppg with the extension mode set to sym and compare with the previous result.

[cAsym,cDsym] = dwt(noisdoppg,'db2','mode','sym');
[max(abs(cA-cAsym)) max(abs(cD-cDsym))]

ans =

     0     0

An unsupported extension mode specified as an input argument is converted to 'sym'. Confirm that taking the DWT of noisdoppg with 'mode' set to an unsupported mode also defaults to the sym extension mode.

[cA,cD] = dwt(noisdoppg,'db2','mode','spd');
[max(abs(cA-cAsym)) max(abs(cD-cDsym))]

ans =

     0     0

Change the current extension mode to periodic. Obtain the single-level discrete wavelet transform of the signal on the GPU using the db2 wavelet.

dwtmode('per','nodisp')
[cA,cD] = dwt(noisdoppg,'db2');

Confirm the current extension mode per is supported for gpuArray input.

[cAper,cDper] = dwt(noisdopp,'db2','mode','per');
[max(abs(cA-cAper)) max(abs(cD-cDper))]

ans =

     0     0

Restore the extension mode to the original setting.

dwtmode(origMode,'nodisp')

Input Arguments

collapse all

`x` — Input data
vector

Input data, specified as a vector.

Data Types: single | double
Complex Number Support: Yes

`wname` — Analyzing wavelet
character vector | string scalar

Analyzing wavelet used to compute the single-level DWT, specified as a character vector or string scalar. The wavelet must be recognized by wavemngr. The analyzing wavelet is from one of the following wavelet families: Best-localized Daubechies, Beylkin, Coiflets, Daubechies, Fejér-Korovkin, Haar, Han linear-phase moments, Morris minimum-bandwidth, Symlets, Vaidyanathan, Discrete Meyer, Biorthogonal, and Reverse Biorthogonal. See wfilters for the wavelets available in each family.

Example: 'db4'

`LoD,HiD` — Wavelet decomposition filters
even-length real-valued vectors

Wavelet decomposition filters, specified as a pair of even-length real-valued vectors. LoD is the lowpass decomposition filter, and HiD is the highpass decomposition filter. The lengths of LoD and HiD must be equal. See wfilters for additional information.

Data Types: single | double

`extmode` — Extension mode
`'zpd'` | `'sp0'` | `'spd'` | ...

Extension mode used when performing the DWT, specified as one of the following:

`mode`	DWT Extension Mode
`'zpd'`	Zero extension
`'sp0'`	Smooth extension of order 0
`'spd'` (or `'sp1'`)	Smooth extension of order 1
`'sym'` or `'symh'`	Symmetric extension (half point): boundary value symmetric replication
`'symw'`	Symmetric extension (whole point): boundary value symmetric replication
`'asym'` or `'asymh'`	Antisymmetric extension (half point): boundary value antisymmetric replication
`'asymw'`	Antisymmetric extension (whole point): boundary value antisymmetric replication
`'ppd'`	Periodized extension (1)
`'per'`	Periodized extension (2) If the signal length is odd, `wextend` adds to the right an extra sample that is equal to the last value, and performs the extension using the `'ppd'` mode. Otherwise, `'per'` reduces to `'ppd'`. This rule also applies to images.

The global variable managed by dwtmode specifies the default extension mode. See dwtmode for extension mode descriptions.

Example: [cA,cD] = dwt(x,'db4','mode','symw') returns the single-level DWT of x using the order 4 Daubechies extremal phase wavelet and whole point symmetric extension.

Output Arguments

collapse all

`cA` — Approximation coefficients
vector

Approximation coefficients obtained from the wavelet decomposition, returned as a vector. Convolving the input signal x with the scaling filter LoD, followed by dyadic decimation, yields the approximation coefficients. Let sx = size(x) and lf = the length of the decomposition filters.

If the DWT extension mode is set to periodization, cA is a vector of length ceil(sx/2).
For the other extension modes, cA is a vector of length floor((sx+lf-1)/2).

Data Types: single | double

`cD` — Detail coefficients
vector

Detail coefficients obtained from the wavelet decomposition, returned as a vector. Convolving the input signal x with the wavelet filter HiD, followed by dyadic decimation, yields the detail coefficients. Let sx = size(x) and lf = the length of the decomposition filters.

If the DWT extension mode is set to periodization, cD is a vector of length ceil(sx/2).
For the other extension modes, cD is a vector of length floor((sx+lf-1)/2).

Data Types: single | double

Algorithms

Starting from a signal s of length N, two sets of coefficients are computed: approximation coefficients cA₁, and detail coefficients cD₁. Convolving s with the scaling filter LoD, followed by dyadic decimation, yields the approximation coefficients. Similarly, convolving s with the wavelet filter HiD, followed by dyadic decimation, yields the detail coefficients.

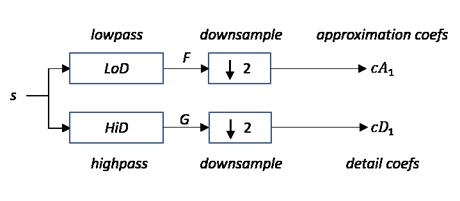
where

— Convolve with filter X
$\begin{matrix} ↓ 2 \end{matrix}$ — Downsample (keep the even-indexed elements)

The length of each filter is equal to 2n. If N = length(s), the signals F and G are of length N + 2n −1 and the coefficients cA₁ and cD₁ are of length floor $(\frac{N - 1}{2}) + n$ .

To deal with signal-end effects resulting from a convolution-based algorithm, a global variable managed by dwtmode defines the kind of signal extension mode used. The possible options include zero-padding and symmetric extension, which is the default mode.

Note

For the same input, the dwt function and the DWT block in the DSP System Toolbox™ do not produce the same results. The DWT block is designed for real-time implementation while Wavelet Toolbox™ software is designed for analysis, so the products handle boundary conditions and filter states differently.

To make the dwt function output match the DWT block output, set the function boundary condition to zero-padding by typing dwtmode('zpd') at the MATLAB^® command prompt. To match the latency of the DWT block, which is implemented using FIR filters, add zeros to the input of the dwt function. The number of zeros you add must be equal to half the filter length.

References

[1] Daubechies, I. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics. Philadelphia, PA: Society for Industrial and Applied Mathematics, 1992.

[2] Mallat, S. G. “A Theory for Multiresolution Signal Decomposition: The Wavelet Representation.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 11, Issue 7, July 1989, pp. 674–693.

[3] Meyer, Y. Wavelets and Operators. Translated by D. H. Salinger. Cambridge, UK: Cambridge University Press, 1995.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

The input wname must be constant.

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Usage notes and limitations:

The input wname must be constant.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

The dwt function supports GPU array input with these usage notes and limitations:

dwt supports only the 'sym' and 'per' extension modes. See dwtmode.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced before R2006a

dwt

Syntax

Description

Examples

DWT Using Wavelet Name

DWT Using Wavelet and Scaling Filters

Single-Level Discrete Wavelet Transform on a GPU

Input Arguments

x — Input data vector

wname — Analyzing wavelet character vector | string scalar

LoD,HiD — Wavelet decomposition filters even-length real-valued vectors

extmode — Extension mode 'zpd' | 'sp0' | 'spd' | ...

Output Arguments

cA — Approximation coefficients vector

cD — Detail coefficients vector

Algorithms

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

GPU Code Generation Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

GPU Arrays Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Version History

See Also

`x` — Input data
vector

`wname` — Analyzing wavelet
character vector | string scalar

`LoD,HiD` — Wavelet decomposition filters
even-length real-valued vectors

`extmode` — Extension mode
`'zpd'` | `'sp0'` | `'spd'` | ...

`cA` — Approximation coefficients
vector

`cD` — Detail coefficients
vector

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.