Main Content

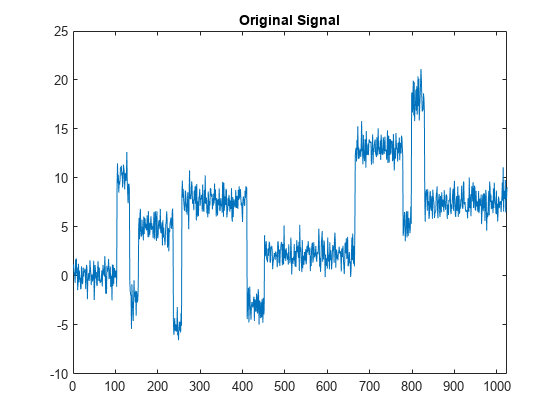
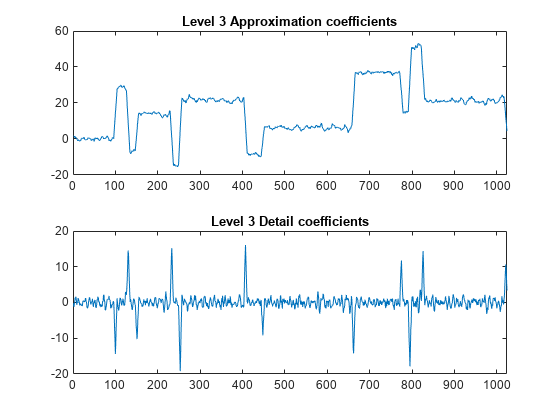
swt

Discrete stationary wavelet transform 1-D

collapse all in page

    Syntax

    swc = swt(x,n,wname)
    swc = swt(x,n,LoD,HiD)
    [swa,swd] = swt(___)

    Description

    swc = swt(x,n,wname) returns the stationary wavelet decomposition of the signal x at level n using the wavelet wname.

    Note

    swt is defined using periodic extension. The length of the approximation and detail coefficients computed at each level equals the length of the signal.

    example

    swc = swt(x,n,LoD,HiD) returns the stationary wavelet decomposition using the specified lowpass and highpass wavelet decomposition filters LoD and HiD, respectively.

    [swa,swd] = swt(___) returns the approximation coefficients swa and stationary wavelet coefficients swd using either of the previous syntaxes.

    Examples

    collapse all

    Open Live Script

    Perform a multilevel stationary wavelet decomposition of a signal.

    Load a one-dimensional signal and acquire its length.

    load noisbloc
s = noisbloc;
sLen = length(s);

    Perform a stationary wavelet decomposition at level 3 of the signal using 'db1'. Extract the detail and approximation coefficients at level 3.

    [swa,swd] = swt(s,3,'db1');
swd3 = swd(3,:);
swa3 = swa(3,:);

    Plot the output of the decomposition.

    plot(s)
xlim([0 sLen])
title('Original Signal')

    Figure contains an axes object. The axes object with title Original Signal contains an object of type line.

    Plot the level 3 approximation and detail coefficients.

    subplot(2,1,1)
plot(swa3)
xlim([0 sLen])
title('Level 3 Approximation coefficients')
subplot(2,1,2)
plot(swd3)
xlim([0 sLen])
title('Level 3 Detail coefficients')

    Figure contains 2 axes objects. Axes object 1 with title Level 3 Approximation coefficients contains an object of type line. Axes object 2 with title Level 3 Detail coefficients contains an object of type line.

    Input Arguments

    collapse all

    Input signal, specified as a real-valued vector.

    Data Types: double

    Level of decomposition, specified as a positive integer. 2n must divide the length of x. Use wmaxlev to determine the maximum level of decomposition.

    Data Types: double

    Analyzing wavelet, specified as a character vector or string scalar. swt supports only Type 1 (orthogonal) or Type 2 (biorthogonal) wavelets. See wfilters for a list of orthogonal and biorthogonal wavelets.

    Wavelet decomposition filters, specified as a pair of even-length real-valued vectors. LoD is the lowpass decomposition filter, and HiD is the highpass decomposition filter. The lengths of LoD and HiD must be equal. See wfilters for additional information.

    Output Arguments

    collapse all

    Stationary wavelet decomposition, returned as a real-valued matrix. The coefficients are stored row-wise:

    • For 1 ≤ i ≤ n, the ith row of swc contains the detail coefficients of level i.

    • swc(n+1,:) contains the approximation coefficients of level n.

    Data Types: double

    Approximation coefficients, returned as a real-valued matrix. For 1 ≤ i ≤ n, the ith row of swa contains the approximation coefficients of level i.

    Data Types: double

    Detail coefficients, returned as a real-valued matrix. For 1 ≤ i ≤ n, the ith row of swd contains the detail coefficients of level i.

    Data Types: double

    Algorithms

    Given a signal s of length N, the first step of the stationary wavelet transform (SWT) produces, starting from s, two sets of coefficients: approximation coefficients cA1 and detail coefficients cD1. These vectors are obtained by convolving s with the lowpass filter LoD for approximation, and with the highpass filter HiD for detail.

    More precisely, the first step is

    where denotes convolution with the filter X.

    Note

    cA1 and cD1 are of length N instead of N/2 as in the DWT case.

    The next step splits the approximation coefficients cA1 in two parts using the same scheme, but with modified filters obtained by upsampling the filters used for the previous step and replacing s by cA1. Then, the SWT produces cA2 and cD2. More generally,

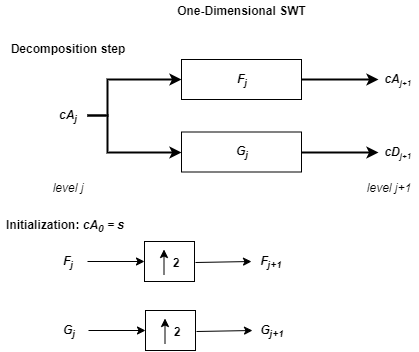
    where

    • F0 = LoD

    • G0 = HiD

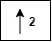    • — Upsample (insert zeros between elements)

    References

    [1] Nason, G. P., and B. W. Silverman. “The Stationary Wavelet Transform and Some Statistical Applications.” In Wavelets and Statistics, edited by Anestis Antoniadis and Georges Oppenheim, 103:281–99. New York, NY: Springer New York, 1995. https://doi.org/10.1007/978-1-4612-2544-7_17.

    [2] Coifman, R. R., and D. L. Donoho. “Translation-Invariant De-Noising.” In Wavelets and Statistics, edited by Anestis Antoniadis and Georges Oppenheim, 103:125–50. New York, NY: Springer New York, 1995. https://doi.org/10.1007/978-1-4612-2544-7_9.

    [3] Pesquet, J.-C., H. Krim, and H. Carfantan. “Time-Invariant Orthonormal Wavelet Representations.” IEEE Transactions on Signal Processing 44, no. 8 (August 1996): 1964–70. https://doi.org/10.1109/78.533717.

    Extended Capabilities

    Version History

    Introduced before R2006a

    See Also

    | | |