filterbank

Joint time-frequency scattering filter bank

Since R2024b

Syntax

[psi1f,psi2f,phift,timemeta] = filterbank(jtfn)

[psifup,psifdown,phiffr,frequencymeta] = filterbank(jtfn,FilterBank="frequency")

Description

[psi1f,psi2f,phift,timemeta] = filterbank(jtfn) returns the first- and second-order time wavelet filter banks, psi1f and psi2f respectively, the time lowpass filter phift, and the metadata timemeta for the time filters in the joint time-frequency scattering (JTFS) network.

example

[psifup,psifdown,phiffr,frequencymeta] = filterbank(jtfn,FilterBank="frequency") returns the spin-up and spin-down frequency wavelets, psifup and psifdown respectively, the frequency lowpass filter phiffr, and the metadata frequencymeta for the frequency filters in the JTFS network.

The syntax filterbank(jtfn,FilterBank="time") is equivalent to filterbank(jtfn).

example

Examples

collapse all

Obtain JTFS Time Wavelet Filter Banks

Open Live Script

Create a JTFS network with the energy correct filters option set to false. Specify quality factors of 9 and 2 for the first-order and second-order time wavelet filter banks, respectively.

jtfn = timeFrequencyScattering(EnergyCorrectFilters=false, ...
    TimeQualityFactors=[9 2]);

Obtain the filters in the first- and second-order time wavelet filter banks and their metadata. Plot the filters. Because the wavelets are analytic, their Fourier transforms are supported only on the positive real axis.

[psi1f,psi2f,phift,timemeta] = filterbank(jtfn);
tiledlayout(2,1)
nexttile
plot(psi1f)
grid on
axis tight
title("First-Order Time Wavelet Filter Bank")
nexttile
plot(psi2f)
grid on
axis tight
title("Second-Order Time Wavelet Filter Bank")

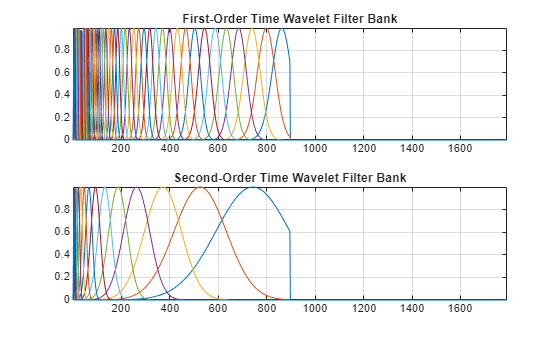
Figure contains 2 axes objects. Axes object 1 with title First-Order Time Wavelet Filter Bank contains 50 objects of type line. Axes object 2 with title Second-Order Time Wavelet Filter Bank contains 15 objects of type line.

Inspect the size and metadata for the first-order time wavelet filter bank. The wavelet filters are arranged columnwise and in order of decreasing center frequency. The $i$ th table row describes the $i$ th filter.

size(psi1f)

ans = 1×2

        1792          50

timemeta{1}

ans=50×6 table
      xi         sigma      isCQT    log2dsfactor    peakidx      bwidx   
    _______    _________    _____    ____________    _______    __________

    0.48076     0.022225      1           0            863      757    897
    0.44512     0.020578      1           0            799      701    896
    0.41212     0.019053      1           0            740      646    833
    0.38158      0.01764      1           0            685      598    771
    0.35329     0.016333      1           0            634      553    714
     0.3271     0.015122      1           0            587      512    661
    0.30286     0.014001      1           0            544      475    613
    0.28041     0.012963      1           0            503      440    567
    0.25962     0.012002      1           0            466      407    525
    0.24038     0.011113      1           0            432      377    486
    0.22256     0.010289      1           0            400      349    450
    0.20606    0.0095263      1           1            370      324    417
    0.19079    0.0088202      1           1            343      300    386
    0.17665    0.0081664      1           1            318      278    358
    0.16355     0.007561      1           1            294      257    331
    0.15143    0.0070006      1           1            272      237    306
      ⋮

Choose a time filter bank. From its metadata, obtain the filter center frequencies and the logical values indicating if a center frequency is logarithmically spaced.

whichFB = 1;
centerFrq = timemeta{whichFB}.xi;
isCQT = timemeta{whichFB}.isCQT;

Compute the ratios of consecutive center frequencies that are logarithmically spaced. Confirm the ratios are equal to $2^{- 1 / Q}$ , where $Q$ is the quality factor of the filter bank.

qualityFactor = jtfn.TimeQualityFactors(whichFB);
isLogSpaced = find(isCQT);
cf = centerFrq(isLogSpaced);
cfRatio = cf(2:end)./cf(1:end-1);
[min(cfRatio) max(cfRatio) 2^(-1/qualityFactor)]

ans = 1×3

    0.9259    0.9259    0.9259

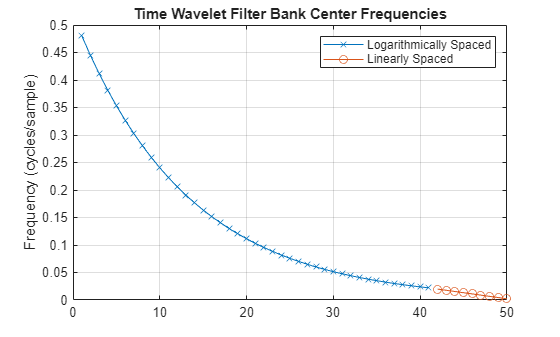
Plot on a linear scale with a cross marker the center frequencies that are logarithmically spaced. Then plot with a circle marker the center frequencies that are linearly spaced.

figure
plot(isLogSpaced,cf,'x-')
hold on
isNotLogSpaced = find(~isCQT);
plot(isNotLogSpaced,centerFrq(isNotLogSpaced),'o-')
hold off
grid on
legend("Logarithmically Spaced","Linearly Spaced")
title("Time Wavelet Filter Bank Center Frequencies")
ylabel("Frequency (cycles/sample)")

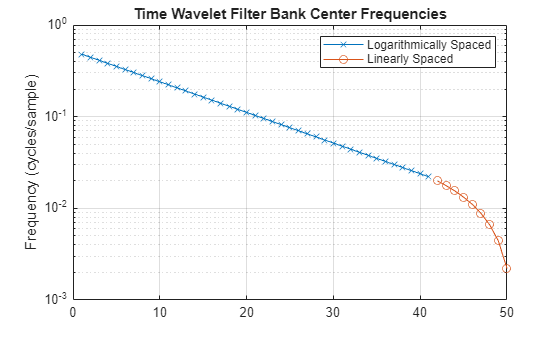
Figure contains an axes object. The axes object with title Time Wavelet Filter Bank Center Frequencies, ylabel Frequency (cycles/sample) contains 2 objects of type line. These objects represent Logarithmically Spaced, Linearly Spaced.

Make the same plot, but this time on a logarithmic scale.

figure
semilogy(isLogSpaced,centerFrq(isLogSpaced),'x-')
hold on
semilogy(isNotLogSpaced,centerFrq(isNotLogSpaced),'o-')
hold off
grid on
legend("Logarithmically Spaced","Linearly Spaced")
title("Time Wavelet Filter Bank Center Frequencies")
ylabel("Frequency (cycles/sample)")

Obtain JTFS Frequency Wavelet Filters

Open Live Script

Create a JTFS network with the energy correct filters option set to false. Specify a frequency quality factor of 3.

jtfn = timeFrequencyScattering(EnergyCorrectFilters=false, ...
    FrequencyQualityFactor=3)

jtfn = 
  timeFrequencyScattering with properties:

                 SignalLength: 1024
          NumFrequencyOctaves: 3
     FrequencyInvarianceScale: 8
       FrequencyQualityFactor: 3
          TimeInvarianceScale: 128
           TimeQualityFactors: [8 1]
         TimeMaxPaddingFactor: 2
               NumTimeOctaves: [7 7]
               FilterDataType: 'double'
    FrequencyMaxPaddingFactor: 2
         EnergyCorrectFilters: 0

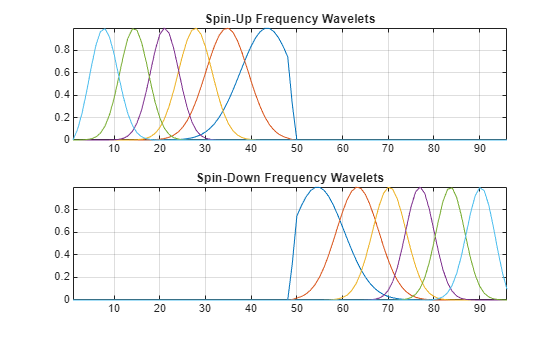
Obtain the spin-up and spin-down frequency wavelets and their metadata. Plot the wavelets.

[psifup,psifdown,phiffr,frequencymeta] = filterbank(jtfn, ...
    FilterBank="frequency");
tiledlayout(2,1)
nexttile
plot(psifup)
grid on
title("Spin-Up Frequency Wavelets")
axis tight
nexttile
plot(psifdown)
title("Spin-Down Frequency Wavelets")
grid on
axis tight

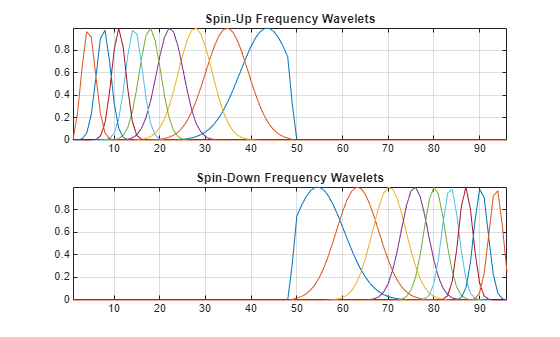
Figure contains 2 axes objects. Axes object 1 with title Spin-Up Frequency Wavelets contains 9 objects of type line. Axes object 2 with title Spin-Down Frequency Wavelets contains 9 objects of type line.

Inspect the metadata. The metadata is listed in order of decreasing center frequency, first for the spin-up wavelets, and then the spin-down wavelets.

frequencymeta

frequencymeta=18×7 table
       xi        sigma      isCQT    log2dsfactor    spin    peakidx     bwidx  
    ________    ________    _____    ____________    ____    _______    ________

     0.44249    0.061128      1           0            1       43       28    49
     0.35121    0.048518      1           0            1       35       22    47
     0.27875    0.038508      1           0            1       28       18    38
     0.22125    0.030564      1           0            1       22       14    30
      0.1756    0.024259      1           1            1       18       12    24
     0.13938    0.019254      1           1            1       14       10    19
     0.10453     0.01625      0           1            1       11        7    15
    0.069688     0.01625      0           2            1        8        4    12
    0.034844     0.01625      0           2            1        4        2     8
    -0.44249    0.061128      1           0           -1       55       49    70
    -0.35121    0.048518      1           0           -1       63       51    76
    -0.27875    0.038508      1           0           -1       70       60    80
    -0.22125    0.030564      1           0           -1       76       68    84
     -0.1756    0.024259      1           1           -1       80       74    86
    -0.13938    0.019254      1           1           -1       84       79    88
    -0.10453     0.01625      0           1           -1       87       83    91
      ⋮

Obtain the center quefrencies of the spin-up wavelets and the logical value indicating if a center quefrency is logarithmically spaced.

numRows = size(frequencymeta,1);
centerQf = frequencymeta.xi(1:numRows/2);
isCQT = frequencymeta.isCQT(1:numRows/2);

Compute the ratios of consecutive center quefrencies that are logarithmically spaced. Confirm the ratios are equal to $2^{- 1 / Q}$ , where $Q$ is the quality factor of the filter bank.

qualityFactor = jtfn.FrequencyQualityFactor;
isLogSpaced = find(isCQT);
cf = centerQf(isLogSpaced);
cfRatio = cf(2:end)./cf(1:end-1);
[min(cfRatio) max(cfRatio) 2^(-1/qualityFactor)]

ans = 1×3

    0.7937    0.7937    0.7937

By default, the number of frequency octaves is 3. Create a second network identical to the first, but instead set the number of frequency octaves to 2. Obtain the frequency wavelets and their metadata. Plot the spin-up and spin-down wavelets. The length and number of frequency wavelets is less than those in the original JTFS network.

jtfn2 = timeFrequencyScattering(EnergyCorrectFilters=false, ...
    FrequencyQualityFactor=3, ...
    NumFrequencyOctaves=2);
[psifup2,psifdown2,~,frequencymeta2] = filterbank(jtfn2, ...
    FilterBank="frequency");
tiledlayout(2,1)
nexttile
plot(psifup2)
grid on
title("Spin-Up Frequency Wavelets")
axis tight
nexttile
plot(psifdown2)
title("Spin-Down Frequency Wavelets")
grid on
axis tight

Figure contains 2 axes objects. Axes object 1 with title Spin-Up Frequency Wavelets contains 6 objects of type line. Axes object 2 with title Spin-Down Frequency Wavelets contains 6 objects of type line.

Input Arguments

collapse all

`jtfn` — Joint time-frequency scattering network
`timeFrequencyScattering` object

Joint time-frequency scattering network, specified as a timeFrequencyScattering object.

Output Arguments

collapse all

Time Wavelet Filter Banks

`psi1f` — First-order time wavelet filter bank
matrix

First-order time wavelet filter bank in the JTFS network, returned as a matrix. The wavelet filters are arranged columnwise and in order of decreasing center frequency.

`psi2f` — Second-order time wavelet filter bank
matrix

Second-order time wavelet filter bank in the JTFS network, returned as a matrix. The wavelet filters are arranged columnwise and in order of decreasing center frequency.

`phift` — Time lowpass filter
vector

Time lowpass filter in the JTFS network, returned as a vector.

`timemeta` — Time filter bank metadata
cell array

Time filter bank metadata, returned as a two-element cell array. The ith element is a MATLAB^® table that describes the ith-order time filter bank. Both tables have these variables:

xi — Wavelet center frequency (cycles/sample)
sigma — Frequency standard deviation
isCQT — Logical value indicating if center frequency is logarithmically spaced
log2dsfactor — Maximum downsampling factor on a base-2 logarithmic scale
peakidx — Center frequency location (one-based index)
bwidx — Total bandwidth used to determine maximum downsampling factor

Frequency Filter Bank

`psifup` — Spin-up frequency wavelets
matrix

Spin-up frequency wavelets in the JTFS network, returned as a matrix. The wavelet filters are arranged columnwise and in order of decreasing center quefrency.

`psifdown` — Spin-down frequency wavelets
matrix

Spin-down frequency wavelets in the JTFS network, returned as a matrix. The wavelet filters are arranged columnwise and in order of decreasing center quefrency.

`phiffr` — Frequency lowpass filter
vector

Frequency lowpass filter in the JTFS network, returned as a vector.

`frequencymeta` — Frequency wavelet metadata
table

Frequency wavelet metadata, returned as a MATLAB table with these variables:

xi — Wavelet center quefrency (cycles/octave)
sigma — Quefrency standard deviation
isCQT — Logical value indicating if center quefrency is logarithmically spaced
log2dsfactor — Maximum downsampling factor on a base-2 logarithmic scale
spin — Spin-up (1) or spin-down (-1) wavelet
peakidx — Center quefrency location (one-based index)
bwidx — Total bandwidth used to determine maximum downsampling factor

Version History

Introduced in R2024b

filterbank

Syntax

Description

Examples

Obtain JTFS Time Wavelet Filter Banks

Obtain JTFS Frequency Wavelet Filters

Input Arguments

`jtfn` — Joint time-frequency scattering network
`timeFrequencyScattering` object

Output Arguments

`psi1f` — First-order time wavelet filter bank
matrix

`psi2f` — Second-order time wavelet filter bank
matrix

`phift` — Time lowpass filter
vector

`timemeta` — Time filter bank metadata
cell array

`psifup` — Spin-up frequency wavelets
matrix

`psifdown` — Spin-down frequency wavelets
matrix

`phiffr` — Frequency lowpass filter
vector

`frequencymeta` — Frequency wavelet metadata
table

Version History

See Also

Objects

Functions

filterbank

Syntax

Description

Examples

Obtain JTFS Time Wavelet Filter Banks

Obtain JTFS Frequency Wavelet Filters

Input Arguments

jtfn — Joint time-frequency scattering network timeFrequencyScattering object

Output Arguments

psi1f — First-order time wavelet filter bank matrix

psi2f — Second-order time wavelet filter bank matrix

phift — Time lowpass filter vector

timemeta — Time filter bank metadata cell array

psifup — Spin-up frequency wavelets matrix

psifdown — Spin-down frequency wavelets matrix

phiffr — Frequency lowpass filter vector

frequencymeta — Frequency wavelet metadata table

Version History

See Also

Objects

Functions

`jtfn` — Joint time-frequency scattering network
`timeFrequencyScattering` object

`psi1f` — First-order time wavelet filter bank
matrix

`psi2f` — Second-order time wavelet filter bank
matrix

`phift` — Time lowpass filter
vector

`timemeta` — Time filter bank metadata
cell array

`psifup` — Spin-up frequency wavelets
matrix

`psifdown` — Spin-down frequency wavelets
matrix

`phiffr` — Frequency lowpass filter
vector

`frequencymeta` — Frequency wavelet metadata
table