Build Wavelet Tree Objects
The following sections explain how to extend the toolbox with new objects through four examples.
Building a Wavelet Tree Object (WTREE)
This example creates a new class of objects: WTREE.
Starting from the class DTREE and overloading the methods split and merge,
we define a wavelet tree class.
To plot a WTREE, the DTREE plot method is
used.
The definition of the new class is described below.
Class WTREE (parent class: DTREE)
Fields
dtree | Parent object |
dwtMode | DWT extension mode |
wavInfo | Structure (wavelet information) |
wavInfo Structure information
wavName | Wavelet Name |
Lo_D | Low Decomposition filter |
Hi_D | High Decomposition filter |
Lo_R | Low Reconstruction filter |
Hi_R | High Reconstruction filter |
Methods
wtree | Constructor for the class WTREE. |
merge | Merge (recompose) the data of a node. |
split | Split (decompose) the data of a terminal node. |
Working With Wavelet Tree Objects (WTREE)
1-D Object
Load a signal.
load noisbloc
x = noisbloc;Define the level and the wavelet.
lev = 3;
wav = 'db2';Create the wavelet tree.
t = wtree(x,lev,wav);
Plot the wavelet tree. The approximations are labeled in yellow and the details are labeled in red. The detail nodes cannot be split.
plot(t)

Change Node Label from Visualize to Split-Merge, and then click node (7), to get this figure:

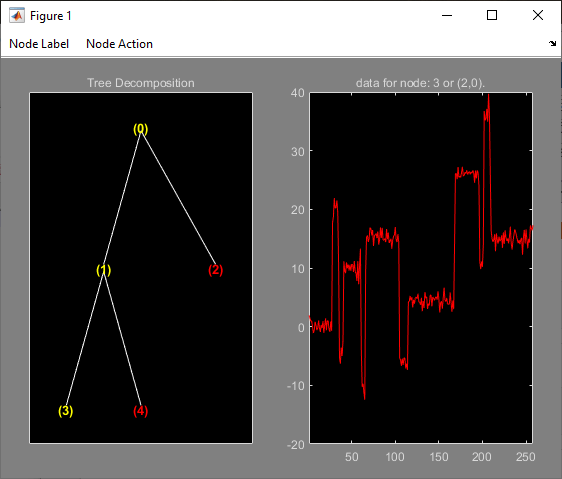
Change Node Action from Visualize to Split-Merge, and merge node (3). Then change Node Action from Split-Merge to Visualize, and click node (3) to get this figure:
2-D Object
Load an image.
load womanDefine the level and the wavelet.
lev = 2;
wav = 'db2';Create the wavelet tree.
t = wtree(X,lev,wav);
Plot the tree.
plot(t)
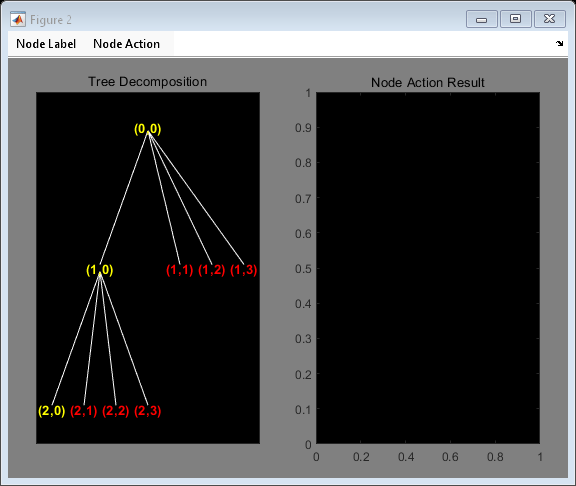
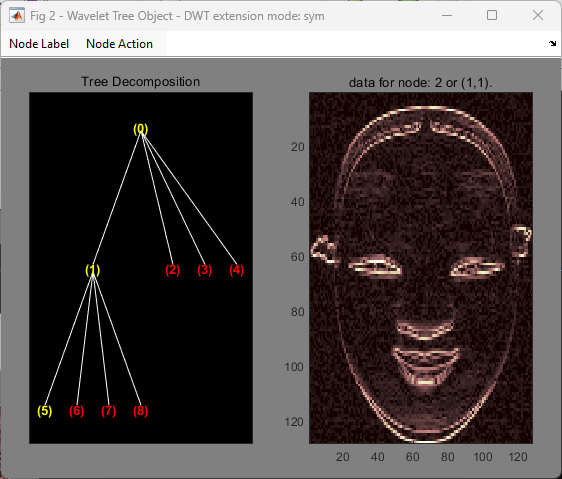
Change Node Label from Depth_Position to Index. Click the node (5). You get the following plot.

Click the node (2). You obtain the following plot.

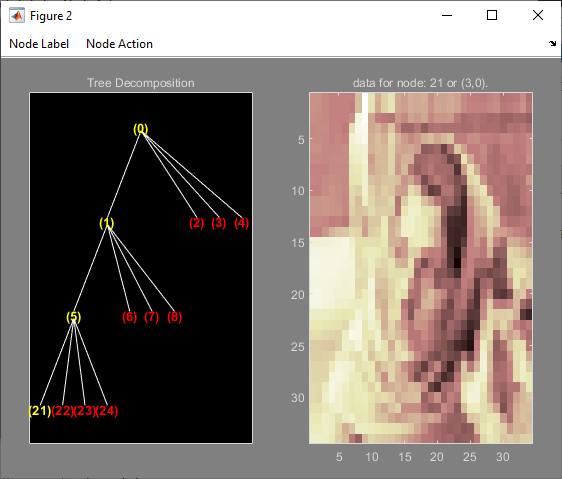
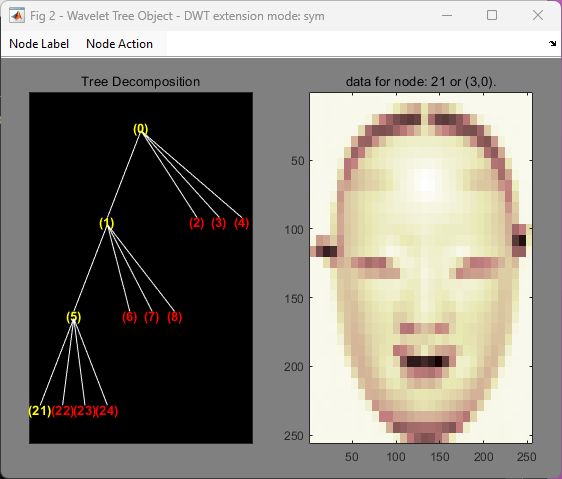
Change Node Action from Visualize to Split-Merge. Split the node (5). Change Node Action from Split-Merge to Visualize. Click the node (21). You obtain the following plot.
Building a Right Wavelet Tree Object (RWVTREE)
This example creates a new class of objects: RWVTREE.
We define a right wavelet tree class starting from the class
WTREE and overloading the methods split, merge,
and plot (inherited from DTREE).
The plot method shows how to add Node Labels.
The definition of the new class is described below.
Class RWVTREE (parent class: WTREE)
Fields
dummy | Not used |
wtree | Parent object |
Methods
rwvtree | Constructor for the class RWVTREE. |
merge | Merge (recompose) the data of a node. |
plot | Plot RWVTREE object. |
split | Split (decompose) the data of a terminal node. |
Working With Right Wavelet Tree Objects (RWVTREE)
1-D Object
Load a signal.
load noisbloc
x = noisbloc;Define the level and the wavelet.
lev = 3;
wav = 'db2';Create the wavelet tree.
t = rwvtree(x,lev,wav);
Plot the tree. The approximations are labeled in yellow and the details are labeled in red. The detail nodes cannot be split.
plot(t)

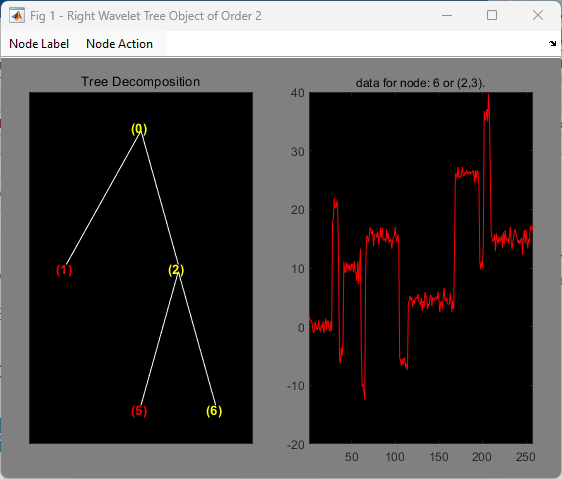
Change Node Action from Visualize to Split-Merge. Merge the node (6). Change Node Action from Split-Merge to Visualize. Click the node (6). You obtain the following plot.
2-D Object
Load an image.
load maskDefine the level and the wavelet.
lev = 2;
wav = 'db2';Create the wavelet tree.
t = wtree(X,lev,wav);
Plot the tree.
plot(t)
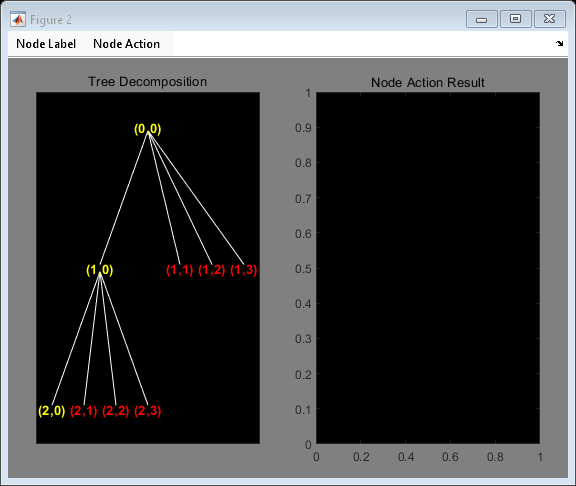
Click the node (2,0). You get the following plot.

Change Node Action from Visualize to Split-Merge. Split the node (2,0). Change Node Action from Split-Merge to Visualize. Click the node (3,0). You obtain the following plot.
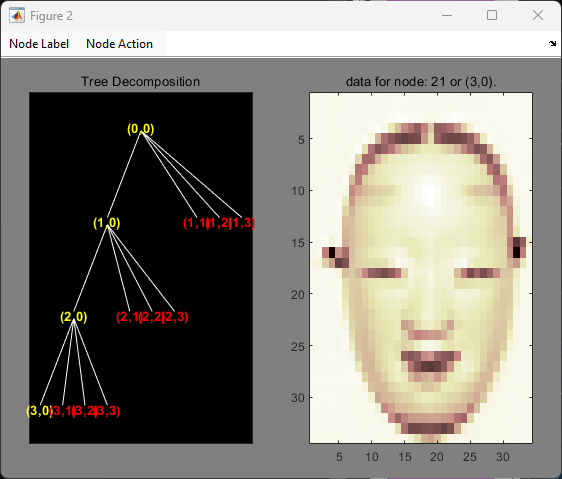
Building a Wavelet Tree Object (WVTREE)
This example creates a new class of objects: WVTREE.
We define a wavelet tree class starting from the class WTREE
and overloading the methods get, plot,
and recons (all inherited from DTREE).
The split and merge methods
of the class WTREE are used.
The plot method shows how to add Node Labels and Node
Actions.
The definition of the new class is described below.
Class WVTREE (parent class: WTREE)
Fields
dummy | Not used |
wtree | Parent object |
Methods
wvtree | Constructor for the class WVTREE. |
get | Get WVTREE object field contents. |
plot | Plot WVTREE object. |
recons | Reconstruct node coefficients. |
Working With Wavelet Tree Objects (WVTREE)
1-D Object
Load the signal.
load noisbloc
x = noisbloc;Define the level and the wavelet.
lev = 3;
wav = 'db2';Create the wavelet tree.
t = wvtree(x,lev,wav);
Plot the tree. The approximations are labeled in yellow and the details are labeled in red. The detail nodes cannot be split.
plot(t)

Change Node Action from Visualize to Split-Merge. Merge the node (3). Change Node Action from Split-Merge to Reconstruct. Click the node (3). You obtain the following plot.
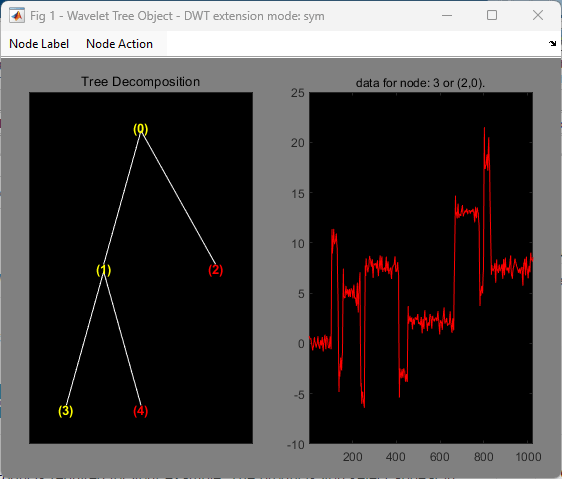
2-D Object
Load an image.
load maskDefine the level and the wavelet.
lev = 2;
wav = 'db1';Create the wavelet tree.
t = wvtree(X,lev,wav);
Plot the tree.
plot(t)

Click the node (5). You get the following plot.
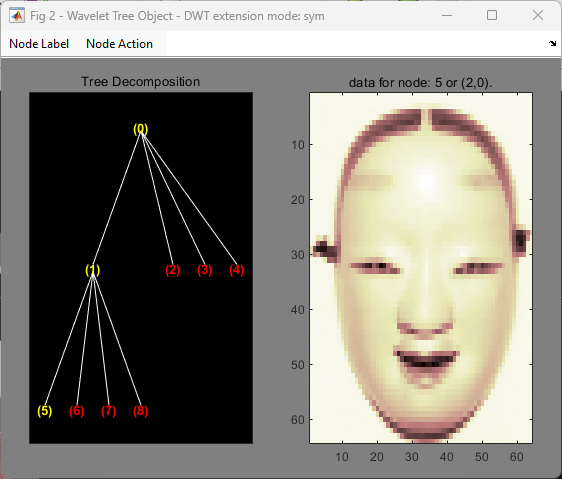
Click the node (2). You obtain the following plot.
Change Node Action from Visualize to Split-Merge. Split the node (5). Change Node Action from Split-Merge to Reconstruct. Click the node (21). You obtain the following plot.
Building a Wavelet Tree Object (EDWTTREE)
This example creates a new class of objects: EDWTTREE.
We define an ε-DWT tree class starting from the class
DTREE and overloading the methods merge, plot, recons,
and split.
For more information on the ε-DWT, see the section ε-Decimated DWT.
The plot method shows how to add Node Labels, Node Actions,
and Tree Actions.
The definition of the new class is described below.
Class EDWTTREE (parent class: DTREE)
Fields
dtree | Parent object |
dwtMode | DWT extension mode |
wavInfo | Structure (wavelet information) |
Fields Description
wavInfo
wavName | Wavelet Name |
Lo_D | Low Decomposition filter |
Hi_D | High Decomposition filter |
Lo_R | Low Reconstruction filter |
Hi_R | High Reconstruction filter |
Methods
edwttree | Constructor for the class EDWTTREE. |
merge | Merge (recompose) the data of a node. |
plot | Plot EDWTTREE object. |
recons | Reconstruct node coefficients. |
split | Split (decompose) the data of a terminal node. |
Working With Wavelet Tree Object (EDWTTREE)
Load the signal.
load noisbloc
x = noisbloc;Define the level and the wavelet.
lev = 2;
wav = 'haar';Create the wavelet tree.
t = edwttree(x,lev,wav);
Plot the tree. The approximations are labeled in yellow and the details are labeled in red. The detail nodes cannot be split. The title of the figure contains the DWT extension mode used ('per' in the present example) and the name of the denoising method.
plot(t)
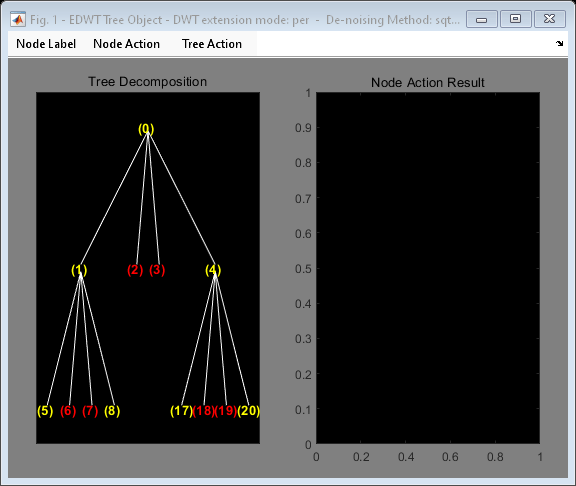
Click the node (0). You obtain the following plot.

Change Node Action from Visualize to Split-Merge. Split the nodes (5) and (20).

Select Tree Action: De-noise. Click the node (0). You obtain the following plot.
