function outdata = PE( indata, delay, order, windowSize )
computes efficiently [1] values of permutation entropy [2] for orders=1...8 of ordinal patterns from 1D time series in sliding windows. See more ordinal-patterns based measures at www.mathworks.com/matlabcentral/fileexchange/63782-ordinal-patterns-based-analysis--beta-version-
NOTES
1 Order of ordinal patterns is defined as in [1,3,7,8], i.e. order = n-1 for n defined as in [2]
2 The values of permutation entropy are normalised by log((order+1)!) so that they are from [0,1] as proposed in the original paper [2].
INPUT
- indata - 1D time series (1 x N points)
- delay - delay between points in ordinal patterns (delay = 1 means successive points)
- order - order of the ordinal patterns (order + 1 is the number of points in ordinal patterns)
- windowSize - size of sliding window ( = number of ordinal patterns within sliding window)
OUTPUT
- outdata - (1 x (N - windowSize - order*delay) values of permutation entropy within [0,1] since each sliding window contains windowSize ordinal patterns but uses in fact (windowSize + order*delay + 1) points).
INTERPRETATION
The larger the values of permutation entropy (in the range from 0 to 1) are, the higher diversity of ordinal patterns is and the more complex input data are.
CITING THE CODE
[a] Unakafova, V.A., Keller, K., 2013. Efficiently measuring complexity on the basis of real-world data. Entropy, 15(10), 4392-4415.
[b] Unakafova, Valentina (2015). Fast permutation entropy (www.mathworks.com/matlabcentral/fileexchange/44161-permutation-entropy--fast-algorithm-), MATLAB Central File Exchange. Retrieved Month Day, Year.
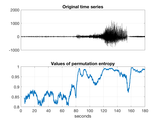
EXAMPLE OF USE (with a plot):
indata = rand( 1, 7777 ); % generate random data points
for i = 4000:7000 % generate change of data complexity
indata( i ) = 4*indata( i - 1 )*( 1 - indata( i - 1 ) );
end
delay = 1; % delay 1 between points in ordinal patterns (successive points)
order = 3; % order 3 of ordinal patterns (4-points ordinal patterns)
windowSize = 512; % 512 ordinal patterns in one sliding window
outdata = PE( indata, delay, order, windowSize );
figure;
ax1 = subplot( 2, 1, 1 ); plot( indata, 'k', 'LineWidth', 0.2 );
grid on; title( 'Original time series' );
ax2 = subplot( 2, 1, 2 );
plot( length(indata) - length(outdata)+1:length(indata), outdata, 'k', 'LineWidth', 0.2 );
grid on; title( 'Values of permutation entropy' );
linkaxes( [ ax1, ax2 ], 'x' );
CHOICE OF ORDER OF ORDINAL PATTERNS
The larger order of ordinal patterns is, the better permutation entropy estimates complexity of the underlying dynamical system [3]. But for time series of finite length too large order of ordinal patterns leads to an underestimation of the complexity because not all ordinal patterns representing the system can occur [3]. Therefore, for practical applications, orders = 3...7 are often used [2,4,5,8].
In [6] the following rule for choice of order is recommended:
5*(order + 1)! < windowSize.
CHOICE OF SLIDING WINDOW LENGTH
Window size should be chosen in such way that time series is stationary within the window (for example, for EEG analysis 2 seconds sliding windows are often used) so that distribution of ordinal patterns would not change within the window [2,8], [3,Section 2.2], [7,Section 5.1.2].
CHOICE OF DELAY BETWEEN POINTS IN ORDINAL PATTERNS
I would recommend choosing different delays and comparing results (see, for example, [3, Section 2.2-2.4] and [7, Chapter 5] for more details) though delay = 1 is often used for practical applications.
Choice of delay depends on particular data analysis you perform [3,4], on type of pre-processing and on sampling rate of the data. For example, if you are interested in low-frequency part of signals it makes sense to use larger delays.
REFERENCES
[1] Unakafova, V.A., Keller, K., 2013. Efficiently measuring complexity on the basis of real-world Data. Entropy, 15(10), 4392-4415.
[2] Bandt, C. and Pompe, B., 2002. Permutation entropy: a natural complexity measure for time series. Physical review letters, 88(17), p.174102.
[3] Keller, K., Unakafov, A.M. and Unakafova, V.A., 2014. Ordinal patterns, entropy, and EEG. Entropy, 16(12), pp.6212-6239.
[4] Riedl, M., Muller, A. and Wessel, N., 2013. Practical considerations of permutation entropy. The European Physical Journal Special Topics, 222(2), pp.249-262.
[5] Zanin, M., Zunino, L., Rosso, O.A. and Papo, D., 2012. Permutation entropy and its main biomedical and econophysics applications: a review. Entropy, 14(8), pp.1553-1577.
[6] Amigo, J.M., Zambrano, S. and Sanjuan, M.A., 2008. Combinatorial detection of determinism in noisy time series. EPL (Europhysics Letters), 83(6), p.60005.
[7] Unakafova, V.A., 2015. Investigating measures of complexity for dynamical systems and for time series (Doctoral dissertation, University of Luebeck).
[8] Keller, K., and M. Sinn. Ordinal analysis of time series. Physica A: Statistical Mechanics and its Applications 356.1 (2005): 114—120
引用格式
Valentina Unakafova (2024). Permutation entropy (fast algorithm) (https://www.mathworks.com/matlabcentral/fileexchange/44161-permutation-entropy-fast-algorithm), MATLAB Central File Exchange. 检索来源 .
MATLAB 版本兼容性
平台兼容性
Windows macOS Linux类别
- Sciences > Neuroscience > Human Brain Mapping > EEG/MEG/ECoG >
- Sciences > Neuroscience > Frequently-used Algorithms >
- Engineering > Biomedical Engineering > Biomedical Signal Processing >
标签
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!| 版本 | 已发布 | 发行说明 | |
|---|---|---|---|
| 1.5.3 | Cover pictures has been updated |
||
| 1.5.2.1 | The files have also been uploaded at GitHub: https://github.com/ValentinaUn/Fast-permutation-entropy |
||
| 1.5.2.0 | Description has been renewed (section INTERPRETATION has been added) |
||
| 1.5.1.0 | Description (NOTES section) has been updated |
||
| 1.5.0.0 | 1 The script is updated for compatibility with MATLAB 2018.
|
||
| 1.4.3.3 | Two variables are renamed in the m-file for consistency. |
||
| 1.4.3.2 | Description has been renewed |
||
| 1.4.3.1 | Description is renewed (notes on parameters choice are added) |
||
| 1.4.3.0 | description is renewed |
||
| 1.4.2.0 | Example of use is corrected |
||
| 1.4.1.0 | Example of use is corrected |
||
| 1.4.0.0 | Example of use is added |
||
| 1.3.0.0 | 1 The values of permutation entropy are divided by order of ordinal patterns
|
||
| 1.2.0.0 | -
|
||
| 1.1.0.0 | A small mistake in the code is corrected:
This mistake introduced a small (~1%) error only in the first WS ePE values if computing for tau>1. |
||
| 1.0.0.0 |