Reinforcement Learning Tutorial: Soft Actor-Critic Control of Robot Arm

In this hands on session, you will learn how to control a robot manipulator, to balance a ball on a plate using reinforcement learning. You will cover the process step by step starting from building the robot model in Simulink to creating and training reinforcement learning agent. Towards the end we will explore a few ways we can customize the RL agent by choosing different algorithms and training options.

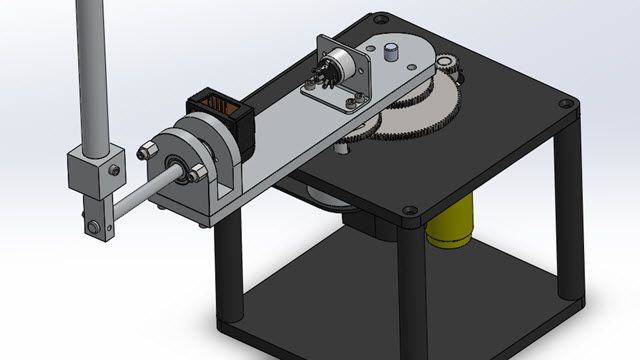
First, let us take a look into the different components of our robot manipulator system. The robot in this example is Kinova robot arm which is a 7 degree of freedom manipulator with a gripper. This diagram shows the modeling of the entire system. The design was created in Simulink using Simscape multi body blocks, which is specifically used to model and simulate high fidelity mechanical systems. Major structural components of the system are the Kinova robot, a flat surface or plate which is attached to the end effector of the robot, and a ping pong ball which can bounce or roll on the plate. Motion of the ball is modeled using a six stop joint but the motion is also restricted by the plate whenever there is contact. The contact force between the ball and plate is modeled using a special contact force block, which basically behaves like a spring and mass temper system.

Now we can look into each of the subsystems to understand them better. In the project folder, you can find a Simulink model under the models folder here. You can open the model and once the model is open, you can navigate under these subsystems and look at them with more detail.

In the robot subsystem, we see the different parts of the robot arm but the links and joints are presented by some skip multi-body blocks. These components are created by importing the CAD geometries or step files using the SM import command. We won't go through the import workflow in detail, but you will find more information on this towards the end of this tutorial.

The revolute joints-- the revel joint blocks are responsible for motion between the links, and the motion is computed after injecting torque signals into the revel joints. For this example, we make it simple by only actuating the last two joints, which is the R6 and R7 joints over here. The other joints remain static at some predefined joint angles. These angles are specified in an initialization script that you can find over here. Can open the script to view the different parameters of the system, and feel free to change anything you like over here.

After getting familiarized with the model, let's take a look into the control problem. In this example, the task is to balance a ping pong ball on the plate. At the beginning of our simulation, the ball can start from any location within the plate, and the control algorithm should calculate the necessary top signals to drive the ball to the center and balance it over there.

This task can be solved using popular control algorithms like MPC or other optimal control methods. However because we need a mathematical model of the plant for such algorithms, designing controllers may become difficult when the system is complex for example, if you were to design an MPC controller for the entire system by actuating all joints, you would need to compute Jacobians or write the transition function for the dynamics which could be a tedious process. This is where reinforcement learning can provide an alternate method for designing controllers.

Here's a quick overview on some key concepts and reinforcement learning. We will focus on the section of reinforcement learning that is known as model free reinforcement learning. As the name suggests, the algorithm does not need the model of the plant, instead the desired behavior is learned by repeated interaction with the plant. This diagram shows the standard data flow in a reinforcement learning setup. The controller in the setup is the RL agent. And the remainder of the system including the robot plate, the ball, and their actuation and sensing components, is known as the environment.

The agent interacts with the environment by providing a set of action signals which is represented by A. The environment uses these signals to step into the next state S which is rendered down to the agent. The agent also receives another signal R from the environment called the reward, which is a feedback on how well the choice of action was suited for the control test.

The goal of the learning algorithm is to maximize this reward over time through repeated interaction of the agent and environment. In this tutorial, we will represent the agent using deep neural networks. You can find more information on designing neural networks in the MATLAB documentation. But for now, let us see how we can use the reinforcement learning tool box to solve the problem.

When you are back in the MATLAB window, open the live script from the project folder here. The script contains a standard command line workflow for reinforcement learning. We begin by running a startup script which adds the necessary files to the MATLAB file and creates the required variables in the base workspace. To run the script, you can click on the Run section button here, and this also opens the Simulink model.

At the top level of this model you will see the reinforcement learning setup that we discussed earlier with the agent exchanging data with environment. Lets navigate into the environment and open the observation subsystem to view the signals. The observation is a set of 22 signals that represents the state of the system at any given time. That includes information on the position and velocities of actuated joints, position and velocity of the ball, of the plate quaternions and the derivatives, and the top inputs from the previous time steps, and then some physical parameters of the ball like mass and radius. The agent will use these observations to compute the actions at every time step. Because these signals have different units, some of them are multiplied with these scale factors so that they remain in more or less the same range as others. It is important because these signals will be fed into a neural network and high magnitude signals may cause one section of the network to dominate and undermine the effect of other signals. The network will train better if you normalize or scale observations in some manner.

We also take the sine and cosine of the orientations instead of using them directly in order to avoid discontinuities of the angles plus or minus 5. This is because discontinuities in the observation space may cause the learning algorithm to converge poorly.

The other signals from the environment is a reward signal. Let us take a few moments to understand the reward signals better. The reward at any time step is given by the relationship shown here. Since we want the agent to move the ball to the center of the plate, we should provide a positive reward when the ball moves to the center. This reward could be the farthest value at any particular state, but we can improve the reward by providing a shape in the form of a non-linear function.

In this case, we use a Gaussian function to reward the agent as the x and y distances of the ball goes to 0. After you have trained the agent a few times, you will find that a well-shaped reward helps in improving training convergence.

In addition to moving the ball to the center, we also want to avoid too much plate orientation, which would be counterintuitive to balancing the ball. For this reason, we provide a penalty for high plate orientation angles. We also provide another penalty to the agent when it uses too much control effort.

Finally we sum the rewards and penalties to obtain the scalar reward at every time step. It is also important to note here that each terminated award function has been multiplied with a scaling factor to specify the relative importance on the overall reward.

The final set of signals from the environment is down signal and determines when the simulation should be terminated. Termination could mean the system has reached a bad state and it does not make sense to simulate further. In this case, we terminate the simulation and the ball falls off the plate by comparing the xy coordinates against the plate boundaries.

Let us go back to the live script to create a reinforcement learning environment from the Simulink model. First you will need to create specifications for the inputs and outputs. Since the observation and action spaces are continuous in our case, you can use that RL numeric spec function to create the specifications as shown here.

Once you have the specifications created, you can create an environment object using the RL Simulink env function as shown here. You will need to specify the Simulink model name, the block path through the RL agent block, and the observation and action specifications that we created before.

One important aspect of training an RL agent is domain randomization. You can randomize the Simulink environment at the beginning of each training episode by providing a function handled to reset the environment as done here. This randomization can help the agent learn a policy that is robust of variations within the environment.

Scroll down to the end of the script to view the reset function. Over here, there are some parameters that may be important for randomization such as the ball physical parameters and the initial joint angles and the initial torques. You can introduce randomness in these parameters as you like. But for now, let's focus on randomizing just the initial versions of the ball and then keep the other parameters constant.

After creating the environment, the next step is to create a reinforcement learning agent in MATLAB. There are many algorithms to choose from in the reinforcement learning tool box. These algorithms work on either discrete or continuous action spaces or both. For this tutorial, you will be using the Soft Actor-Critic agent that supports continuous action space.

Here is a high level explanation of the Soft Actor-Critic algorithm. Guidance in blue represent the major components of the agent. An experienced buffer is used to store experiences from the agent environment interactions and the agent learns by using sample data from this buffer. The learning algorithm for this agent follows the active critic approach with one actor and two critics, each of which are represented by neural networks.

The actor looks at the environment states and selects the actions based on a mean and variance output from the network as shown over here. This mean invariance defines the stochastic policy of the actor and is used to compute the agent's actions. During training, the weights of the actor network are updated by a trade off between the expected reward and the entropy of the policy.

The critics kind of sit behind the actor and criticize the actions whether they're good or bad. Their rates are also updated periodically. The algorithm uses multiple critics to reduce overestimation of the Q function. You can find more information on the Soft Actor-Critic algorithm towards the end of this tutorial. But for now, all you need to do is to create this neural networks in MATLAB. Everything else will be handled by the toolbox.

Now we are back to the line script again. You can create the neural networks by running the code in this section. As shown here, the critic networks consist of a few fullyConnectedLayers with reluLayers in between. The inputs to this network are the observations and actions of the agent. And the output is the Q function value. You can use the same critic network to create the two critics.

The actor is also modeled in a similar way. It takes observations as inputs and outputs the mean and variance of the policy distribution. After creating the actor and critics, you can create the agent using the rlSACAgent function as shown here. Most of the type of parameters of the agent are kept to the default values as shown here. So you need not worry too much about changing them for this tutorial. For a full list of type of parameters, you can click on this link which will take you to the MATLAB documentation.

Once the agent is created, the final step is to train the algorithm using the train command. You can specify a few training options such as how long the agent is going to train and what is a stock value for training. For example, you can set the maximum number of training episodes as shown here and then the maximum steps for training episode.

Another important parameter is the stop training criteria. In this case, we stopped the training when the average reward over the last 100 episodes reaches the value of 675 or more. This value was obtained after analyzing the agent's performance for a few training iterations.

To start the training, you can set this blue training flag to true and execute the code in the section. Software will take a few seconds to set up the training and we'll launch an episode manager figure to keep track of the training progress.

Once the figure launches, you can view the training progress from the plot as well see the animation in the mechanics Explorer window. You can see here that the agent is trying to balance the ball but failing most of the time. This is expected because it is towards the beginning of training and the agent has not learned much.

We'll also see from the plot that the agent does not receive too many rewards per episode. And the figure at the blue line represents the episode reward and the red line represents the average reward over a window of 100 episodes. Yellow line represents the expected long term reward.

As the agent learns from experiences, you will see that the rewards will increase and converge to some value. At that point, you can stop the training and view the agent's performance. To stop the training, you can simply click on the Stop Training button over here. In the interest of time, let's stop the training and continue with the live script.

A snapshot of a completed training session is shown in the figure here. This will give you an idea of what we expect in the training process. For this particular training, the agent reached the average reward of 675 after about 3,300 episodes. It took about 20 hours to complete.

Depending on your system specifications, the training may take less time or more. Also, since there is randomness in the process, your actual results may be a little different from what is shown here. Let's load a pre-trained agent now to view this performance. You can set the doTraining flag back to false to load an agent saved in a MAT file. You can run the section again to load the file.

After loading the agent, scroll down to the simulation section. Here, you can set the initial position of the ball to your liking and simulate the model this time with a trained agent. Over here the initial x and y positions are set to some non-zero values. Let's run the section. You can now see in the animation that the agent is able to center the ball successfully. You can try simulating a few different times with different initial conditions.

Going back to the Simulink model, you can view the trajectory of the ball and the control inputs through these code blocks. As seen here, the x and y trajectories are converged to zero or near-zero values. We can consider this as satisfactory for this tutorial. The actions, on the other hand, seem pretty noisy. And for practical purposes, we may need to consider whether the actuate can handle these signals. We can consider it as a future enhancement for analysis agent's performance. It's consistent with our reward function.

Here are a few options for fine tuning the agent's performance. You can randomize other parameters in the environment like ball mass and initial velocities doing training. You can also change parameters and the reward function, or change the agent hyperparameters. Another option is to use a different agent algorithm for this test. We won't be covering these in this video, but you can try them by yourself and discover more of about reinforcement learning.

That concludes this video. We covered a lot of concepts and hopefully this gave you an insight on RL and how to use the reinforcement learning tool box for solving control problems. Finally, here are some resources that you can use for further reading.