Train SAC Agent for Ball Balance Control

Fix Random Seed Generator to Improve Reproducibility

The example code may involve computation of random numbers at various stages such as initialization of the agent, creation of the actor and critic, resetting the environment during simulations, generating observations (for stochastic environments), generating exploration actions, and sampling min-batches of experiences for learning. Fixing the random number stream preserves the sequence of the random numbers every time you run the code and improves reproducibility of results. You will fix the random number stream at various locations in the example.

Fix the random number stream with the seed 0 and random number algorithm Mersenne Twister. For more information on random number generation see rng.

previousRngState = rng(0,"twister")

previousRngState = struct with fields:
     Type: 'twister'
     Seed: 0
    State: [625x1 uint32]

The output previousRngState is a structure that contains information about the previous state of the stream. You will restore the state at the end of the example.

Environment Overview

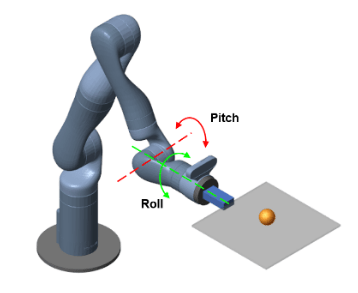
The robot arm in this example is a Kinova Gen3 robot, which is a seven degree-of-freedom (DOF) manipulator. The arm is tasked to balance a ping pong ball at the center of a flat surface (plate) attached to the robot gripper. Only the final two joints are actuated and contribute to motion in the pitch and roll axes as shown in the following figure. The remaining joints are fixed and do not contribute to motion.

Open the Simulink® model to view the system. The model contains a Kinova Ball Balance subsystem connected to an RL Agent block. The agent applies an action to the robot subsystem and receives the resulting observation, reward, and is-done signals.

open_system("rlKinovaBallBalance")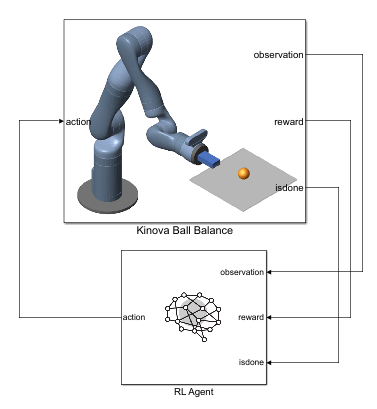

View to the Kinova Ball Balance subsystem.

open_system("rlKinovaBallBalance/Kinova Ball Balance")

In this model:

Create the parameters for the example by running the kinova_params script included with this example.

kinova_params;

You can view a 3-D animation of the manipulator in the Mechanics Explorer with the Robotics System Toolbox Robot Library Data support package. When you have the support package installed, the Script also adds the necessary 3D mesh files to the MATLAB® path. To download and install the support package, use the Add-On Explorer. For more information see Get and Manage Add-Ons.

Create Environment Object

To train a reinforcement learning agent, you must define the environment with which it will interact. For the ball balancing environment:

Here, ${\mathit{r}}_{\mathrm{ball}}$ is a reward for the ball moving closer to the center of the plate, ${\mathit{r}}_{\mathrm{plate}}$ is a penalty for plate orientation, and ${\mathit{r}}_{\mathrm{action}}$ is a penalty for control effort. $\varphi$, $\theta$, and $\psi$ are the respective roll, pitch, and yaw angles of the plate in radians. ${\tau }_1$ and ${\tau }_2$ are the joint torques.

Create the observation and action input specifications for the environment.

nObs = 22;  % Number of dimension of the observation space
nAct = 2;   % Number of dimension of the action space

obsInfo = rlNumericSpec([nObs 1]);

actInfo = rlNumericSpec([nAct 1]);
actInfo.LowerLimit = -1;
actInfo.UpperLimit = 1;

Create the Simulink environment object using the observation and action specifications. For more information on creating Simulink environments, see rlSimulinkEnv.

mdl = "rlKinovaBallBalance";
blk = mdl + "/RL Agent";
env = rlSimulinkEnv(mdl,blk,obsInfo,actInfo);

Specify a reset function for the environment using the ResetFcn parameter. The kinovaResetFcn function is defined at the end of the example.

env.ResetFcn = @kinovaResetFcn;

This kinovaResetFcn function (provided at the end of this example) randomly initializes the initial x and y positions of the ball with respect to the center of the plate. For robust training, you can randomize other parameters inside the reset function, such as the mass and radius of the ball.

Specify the sample time Ts and simulation time Tf.

Ts = 0.01;
Tf = 10;

Create Soft Actor-Critic Agent With Custom Networks

The agent in this example is a soft actor-critic (SAC) agent. SAC agents use one or two parametrized Q-value function approximators to estimate the value of the policy. A Q-value function critic takes the current observation and an action as inputs and returns a single scalar as output (the estimated discounted cumulative long-term reward for which receives the action from the state corresponding to the current observation, and following the policy thereafter). For more information on SAC agents, see Soft Actor-Critic (SAC) Agent.

Create Critic

The SAC agent in this example uses two critics. To model the parametrized Q-value functions within the critics, use a neural network with two input layers (one for the observation channel, as specified by obsInfo, and the other for the action channel, as specified by actInfo) and one output layer (which returns the scalar value). For more information on creating deep neural networks for reinforcement learning agents, see Create Policies and Value Functions.

The initial parameters of the critic network are initialized with random values. Fix the random number stream so that the critic is always initialized with the same parameter values.

rng(0,"twister");

Define each network path as an array of layer objects. Assign names to the input and output layers of each path. These names allow you to connect the paths and then later explicitly associate the network input and output layers with the appropriate environment channel.

% Define the network paths.
observationPath = [
    featureInputLayer(nObs,Name="observation")
    concatenationLayer(1,2,Name="concat")
    fullyConnectedLayer(128)
    reluLayer
    fullyConnectedLayer(64)
    reluLayer
    fullyConnectedLayer(32)
    reluLayer
    fullyConnectedLayer(1,Name="QValueOutLyr")
    ];
actionPath = featureInputLayer(nAct,Name="action");

Assemble dlnetwork object.

criticNet = dlnetwork;
criticNet = addLayers(criticNet, observationPath);
criticNet = addLayers(criticNet, actionPath);
criticNet = connectLayers(criticNet,"action","concat/in2");

View the critic neural network.

plot(criticNet)

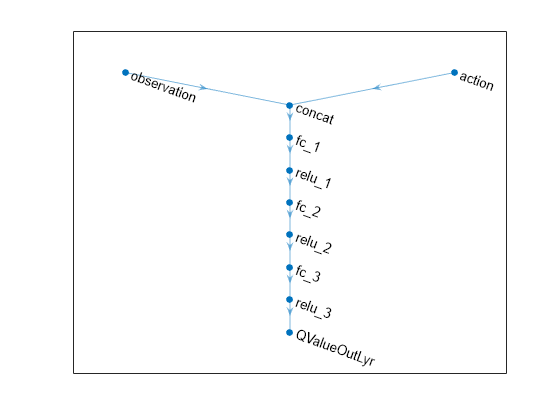
Display the number of weights.

summary(initialize(criticNet))

   Initialized: true

   Number of learnables: 13.5k

   Inputs:
      1   'observation'   22 features
      2   'action'        2 features

Create the critic approximators using rlQValueFunction. When using two critics, a SAC agent requires them to have different initial parameters. Initialize the networks separately to make sure that their initial weights are different.

critic1 = rlQValueFunction(initialize(criticNet), ...
    obsInfo,actInfo, ...
    ObservationInputNames="observation");
critic2 = rlQValueFunction(initialize(criticNet), ...
    obsInfo,actInfo, ...
    ObservationInputNames="observation");

Create Actor

Soft Actor-critic agents use a parametrized stochastic policy over a continuous action space, which is implemented by a continuous Gaussian actor.

This actor takes an observation as input and returns as output a random action sampled from a Gaussian probability distribution.

To approximate the mean values and standard deviations of the Gaussian distribution, you must use a neural network with two output layers, each having as many elements as the dimension of the action space. One output layer must return a vector containing the mean values for each action dimension. The other must return a vector containing the standard deviation for each action dimension.

Since standard deviations must be nonnegative, use a softplus or ReLU layer to enforce nonnegativity. The SAC agent automatically reads the action range from the UpperLimit and LowerLimit properties of actInfo (which is used to create the actor), and then internally scales the distribution and bounds the action. Therefore, do not add a tanhLayer as the last nonlinear layer in the mean output path.

The initial parameters of the actor network are initialized with random values. Fix the random number stream so that the actor is always initialized with the same parameter values.

rng(0,"twister");

Define each network path as an array of layer objects, and assign names to the input and output layers of each path.

% Create the actor network layers.
commonPath = [
    featureInputLayer(nObs,Name="observation")
    fullyConnectedLayer(128)
    reluLayer
    fullyConnectedLayer(64)
    reluLayer(Name="commonPath")
    ];
meanPath = [
    fullyConnectedLayer(32,Name="meanFC")
    reluLayer
    fullyConnectedLayer(nAct,Name="actionMean")
    ];
stdPath = [
    fullyConnectedLayer(nAct,Name="stdFC")
    reluLayer
    softplusLayer(Name="actionStd")
    ];

Assemble dlnetwork object.

actorNet = dlnetwork;
actorNet = addLayers(actorNet,commonPath);
actorNet = addLayers(actorNet,meanPath);
actorNet = addLayers(actorNet,stdPath);
actorNet = connectLayers(actorNet,"commonPath","meanFC/in");
actorNet = connectLayers(actorNet,"commonPath","stdFC/in");

View the actor neural network.

plot(actorNet)

Initialize network and display the number of weights.

actorNet = initialize(actorNet);
summary(actorNet)

   Initialized: true

   Number of learnables: 13.4k

   Inputs:
      1   'observation'   22 features

Create the actor function using rlContinuousGaussianActor.

actor = rlContinuousGaussianActor(actorNet, obsInfo, actInfo, ...
    ObservationInputNames="observation", ...
    ActionMeanOutputNames="actionMean", ...
    ActionStandardDeviationOutputNames="actionStd");

Create Agent Object

The SAC agent in this example trains from an experience buffer of maximum capacity 1e6 by randomly selecting mini-batches of size 256. The fact that the discount factor is 0.99, that is very close to 1, means that the agent keeps more into account long term rewards (a discount factor closer to 0 would instead place a heavier discount on future rewards, therefore encouraging short term ones). For a full list of SAC hyperparameters and their descriptions, see rlSACAgentOptions.

Specify the agent hyperparameters for training. For this example:

agentOpts = rlSACAgentOptions( ...
    SampleTime             = Ts, ...
    ExperienceBufferLength = 1e6, ...
    NumWarmStartSteps      = 1e3, ...
    MiniBatchSize          = 300);

agentOpts.ActorOptimizerOptions.Algorithm = "adam";
agentOpts.ActorOptimizerOptions.LearnRate = 1e-4;
agentOpts.ActorOptimizerOptions.GradientThreshold = 1;

for ct = 1:2
    agentOpts.CriticOptimizerOptions(ct).Algorithm = "adam";
    agentOpts.CriticOptimizerOptions(ct).LearnRate = 5e-4;
    agentOpts.CriticOptimizerOptions(ct).GradientThreshold = 1;
end

Fix the random number stream for reproducibility.

rng(0,"twister");

Create the SAC agent using the actor, critic and agent options objects.

agent = rlSACAgent(actor,[critic1,critic2],agentOpts);

Train Agent

To train the agent, first specify the training options using rlTrainingOptions. For this example, use the following options:

% training options
trainOpts = rlTrainingOptions(...
    MaxEpisodes=6000, ...
    MaxStepsPerEpisode=floor(Tf/Ts), ...
    ScoreAveragingWindowLength=100, ...
    StopTrainingCriteria="EvaluationStatistic", ...
    StopTrainingValue=700, ...
    SimulationStorageType="none");

% agent evaluation
evl = rlEvaluator(EvaluationFrequency=100, NumEpisodes=5);

To train the agent in parallel, specify the following training options. Training in parallel requires Parallel Computing Toolbox™ software. If you do not have Parallel Computing Toolbox™ software installed, set UseParallel to false.

trainOpts.UseParallel = true;
trainOpts.ParallelizationOptions.Mode = "async";

For more information see rlTrainingOptions.

In parallel training, workers simulate the agent's policy with the environment and store experiences in the replay memory. When workers operate asynchronously the order of stored experiences may not be deterministic and can ultimately make the training results different. To maximize the reproducibility likelihood:

You can log training data using the rlDataLogger object. For this example, log the actor and critic training losses using the logAgentLearnData function provided at the end of this example.

logger = rlDataLogger();
logger.AgentLearnFinishedFcn = @logAgentLearnData;

For more information see Log Training Data to Disk.

Fix the random number stream for reproducibility.

rng(0,"twister");

Train the agent using the train function. Training this agent is a computationally intensive process that takes several minutes to complete. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.

doTraining = false;
if doTraining
    % train
    trainResult = train(agent, env, ...
        trainOpts, ...
        Logger    = logger, ...
        Evaluator = evl);
else
    load("kinovaBallBalanceAgent.mat")       
end

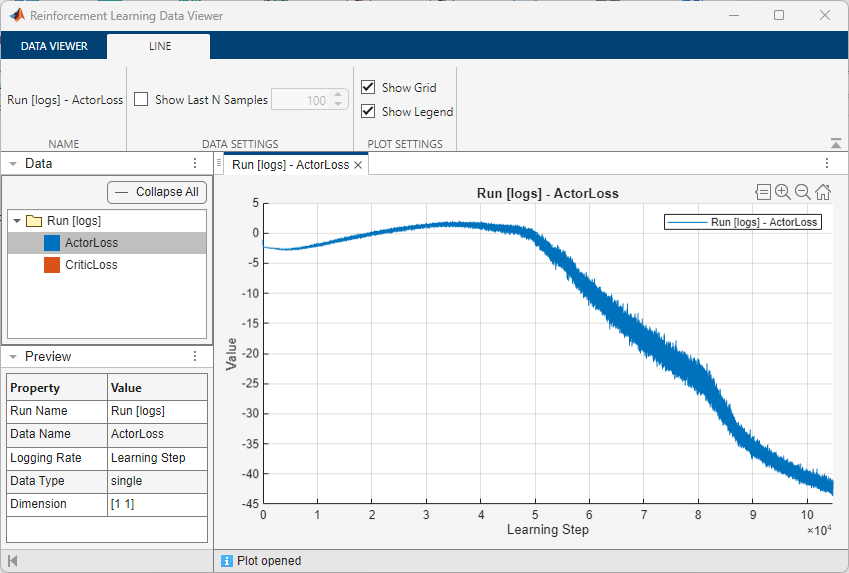
A snapshot of training progress is shown in the following figure. You can expect different results due to randomness in the training process.

You can visualize data logged to disk using the interactive Reinforcement Learning Data Viewer graphical user interface. To open the visualization, click View Logged Data in the Reinforcement Learning Training Monitor window.

To create plots in the Reinforcement Learning Data Viewer, select a data from the Data panel and a choice of plot from the toolstrip. The following images show the actor and critic losses logged during training.

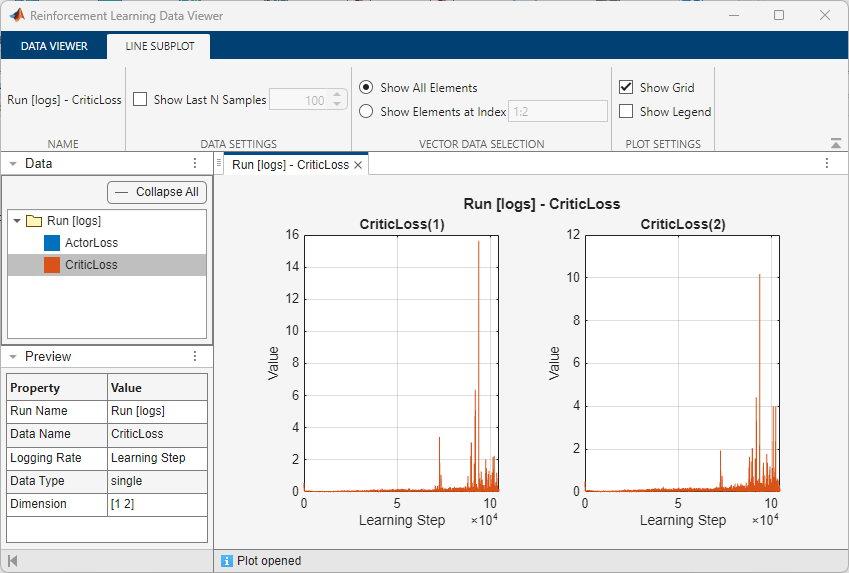
Simulate Trained Agent

Fix the random number stream for reproducibility.

rng(0,"twister");

Specify an initial position for the ball with respect to the plate center. To randomize the initial ball position during simulation, set the userSpecifiedConditions flag to false.

userSpecifiedConditions = true;
if userSpecifiedConditions
    ball.x0 = 0.1;
    ball.y0 = -0.1;
    env.ResetFcn = @(in) setPostSimFcn(in, @animatedPath);
else
    env.ResetFcn = @kinovaResetFcn;
end

Create a simulation options object for configuring the simulation. The agent will be simulated for a maximum of floor(Tf/Ts) steps per simulation episode.

simOpts = rlSimulationOptions(MaxSteps=floor(Tf/Ts));

Simulate the agent using the greedy policy.

agent.UseExplorationPolicy = false;
experiences = sim(agent,env,simOpts);

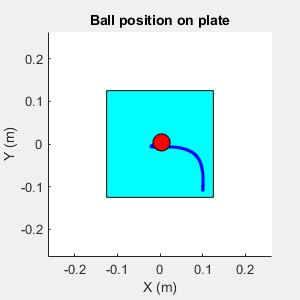
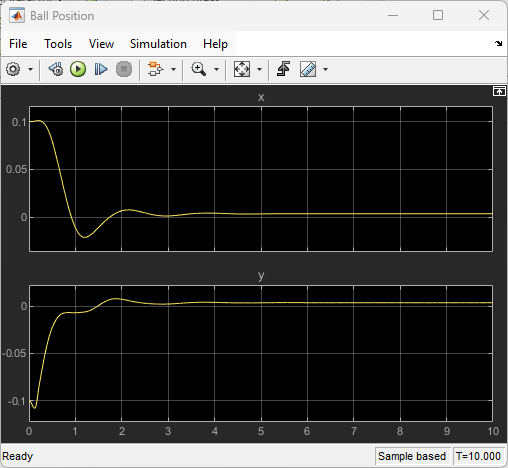
View the trajectory of the ball using the Ball Position scope block.

Restore the random number stream using the information stored in previousRngState.

rng(previousRngState);

Environment Reset Function

function in = kinovaResetFcn(in)
    % KinovaResetFcn is used to randomize 
    % the initial joint angles R6_q0 and R7_q0 as well as 
    % the initial wrist and hand torque values.

    % Ball parameters
    ball.radius = 0.02;     % m
    ball.mass   = 0.0027;   % kg
    ball.shell  = 0.0002;   % m
    
    % Calculate ball moment of inertia.
    ball.moi = calcMOI(ball.radius,ball.shell,ball.mass);
    
    % Initial conditions. +z is vertically upward.
    % Randomize the x and y initial distances (in m) within plate.
    ball.x0  = -0.1 + 0.2*rand;  % x distance from plate center
    ball.y0  = -0.1 + 0.2*rand;  % y distance from plate center
    ball.z0  = ball.radius;      % z height from plate surface
    
    ball.dx0 = 0;   % m/s, ball initial x velocity
    ball.dy0 = 0;   % m/s, ball initial y velocity
    ball.dz0 = 0;   % m/s, ball initial z velocity
    
    % Contact friction parameters
    ball.staticfriction     = 0.5;
    ball.dynamicfriction    = 0.3; 
    ball.criticalvelocity   = 1e-3;
    
    % Convert coefficient of restitution to spring-damper parameters.
    coeff_restitution = 0.89;
    [k, c, w] = cor2SpringDamperParams(coeff_restitution,ball.mass);
    ball.stiffness = k;
    ball.damping = c;
    ball.transitionwidth = w;
    
    in = setVariable(in,"ball",ball);
    
    % Randomize joint angles within a range of +/- 5 deg from the 
    % starting positions of the joints.
    R6_q0 = deg2rad(-65) + deg2rad(-5+10*rand);
    R7_q0 = deg2rad(-90) + deg2rad(-5+10*rand);
    in = setVariable(in,"R6_q0",R6_q0);
    in = setVariable(in,"R7_q0",R7_q0);
    
    % Compute approximate initial joint torques that hold the ball,
    % plate and arm at their initial configuration
    g = 9.80665;
    wrist_torque_0 = ...
        (-1.882 + ball.x0*ball.mass*g)*cos(deg2rad(-65)-R6_q0);
    hand_torque_0 = ...
        (0.0002349 - ball.y0*ball.mass*g)*cos(deg2rad(-90)-R7_q0);
    U0 = [wrist_torque_0 hand_torque_0];
    in = setVariable(in,"U0",U0);

    % specify function to be executed after simulation
    in = setPostSimFcn(in, @animatedPath); % visualization
end

Data Logging Functions

function dataToLog = logAgentLearnData(data)
% This function is executed after completion
% of the agent's learning subroutine.
dataToLog.ActorLoss = data.ActorLoss;
dataToLog.CriticLoss = data.CriticLoss;
end