估计电力电子模型的频率响应
作者 Antonino Riccobono and Arkadiy Turevskiy, MathWorks
本文是系列课程（共三部分）的第一部分。第二部分, 估计电力电子模型的频率响应：正弦流与伪随机二进制序列 (PRBS)，将开环 Buck 变换器的 FRE 与正弦流和 PRBS 进行比较，重点关注估计时间、估计频率点数和估计准确度。下篇《电力电子模型的级联数字 PID 控制设计》描述了基于频率响应估计的控制设计工作流，用于调节具有内层电流控制回路和外层电压控制回路的开关模式 Buck 变换器的控制器增益。
电力电子系统依靠反馈控制，将电源的电压和电流转换至负载所需的水平。举例来说，直流-直流电力变换器使用控制系统来实现所需的输出电压水平，并在电源电压及负载电阻变化时维持电压稳定。
电力电子工程师进行控制设计时，通常以经典控制理论为基础。由于该理论以传递函数和状态空间模型等线性时不变 (LTI) 系统为基础，要将其应用于某一电力电子系统，工程师需要找到该系统的 LTI 表示。
频率响应估计（也称交流扫频）常用于计算电力电子模型的 LTI 表示。频率响应估计将一个振幅和频率可控的小扰动信号迭加到稳态运行系统的输入端，并测量系统对此扰动的响应。测得的输入和输出信号可用于计算频率响应或传递函数，即 LTI 系统，从而基于工况点表示系统动态。
本文介绍开环 Boost 变换器频率响应估计的六步工作流程。
开环 Boost 变换器模型
Boost 变换器是一种十分常见的开关模式变换器，可以产生大于直流输入电压的直流输出电压。该变换器常用于连接低电压电源和高电压负载，应用广泛，包括消费类电子产品、电动汽车、多电舰船和飞行器、可再生能源以及 LED 驱动器。
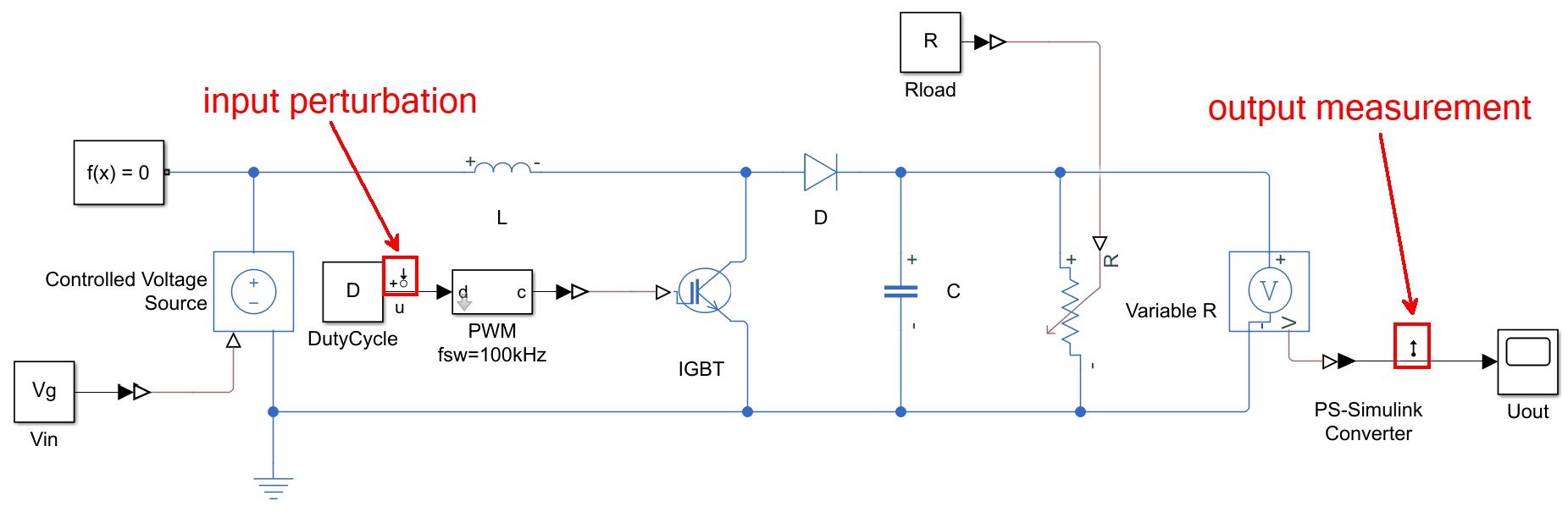
我们的开关模式开环 Boost 变换器模型采用 Simscape Electrical™ 组件构建（图 1）。假设变换器在连续导通模式 (CCM) 下运作，即当变换器以稳态运行时，电感电流始终不为零。在进行频率响应估计时，输入扰动与输出测量点分别设为占空比和输出电压。此时，控制到输出的传递函数以占空比为控制输入，以输出电压为输出。
图 1. 具有输入扰动和输出测量的开关模式开环 Boost 变换器模型。
频率响应估计工作流程
频率响应估计工作流程包含以下六个步骤。
1. 指定模型中的哪一部分需要频率响应估计。
为此，我们使用 Simulink Control Design™ 的 Linearization Manager，配置线性化分析点以指定要估计的输入和输出。我们将输入扰动 (Input Perturbation) 指定为占空比，将输出测量 (Output Measurement) 指定为输出电压（图 2）。
图 2. Linearization Manager 工具栏，已指定线性化点。
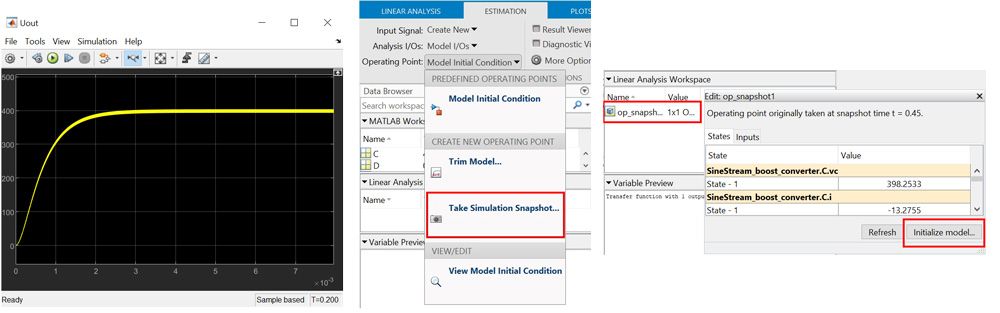
2. 查找工况点并初始化模型。
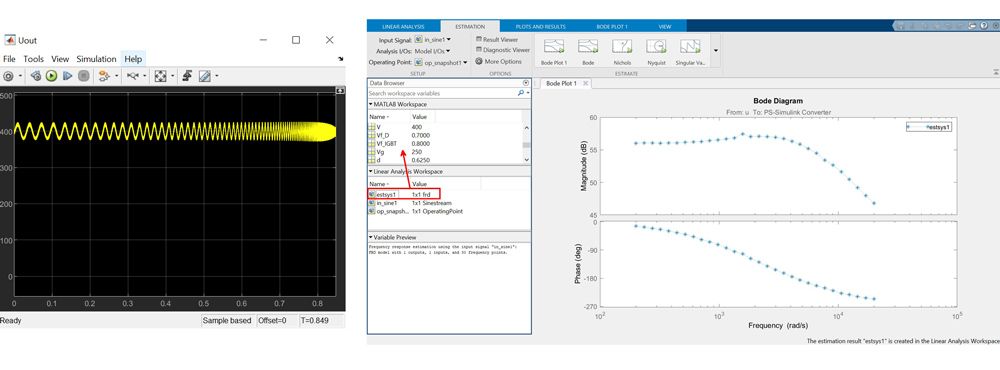
要获得准确捕捉系统动态的频率响应，应当在稳态工况点上执行估计。仿真结果表明，Boost 变换器大约从 0.005 秒起达到稳态（图 3，左）。我们可以在 0.005 秒抓取一张仿真快照，以查找稳态工况点（图 3，中）。仿真结束时，该 App 的工作区中将创建一个 OperatingPoint 对象。我们可以单击 Initialize model 来初始化该对象的模型（图 3，右）。注意：在扰动注入过程中，务必确保没有任何使工况点发生变化的干扰。
图 3.输出电压初始瞬变（左）、仿真快照（中）和模型初始化（右）。
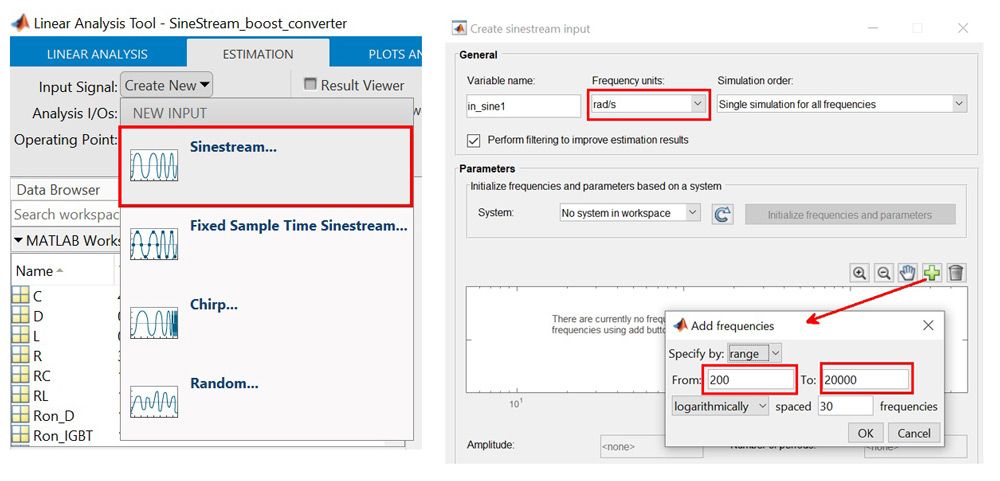
3. 创建扰动信号。
在 Model Linearizer 中，我们选择 sinestream 作为扰动信号。sinestream 信号包含正弦扫频，可在一定周期内激励系统。首先，我们要界定该正弦扫频应覆盖的频率范围（图 4）。
图 4. Frequency Response Estimator，已选择 sinestream 扰动信号（左）和频率范围（右）。
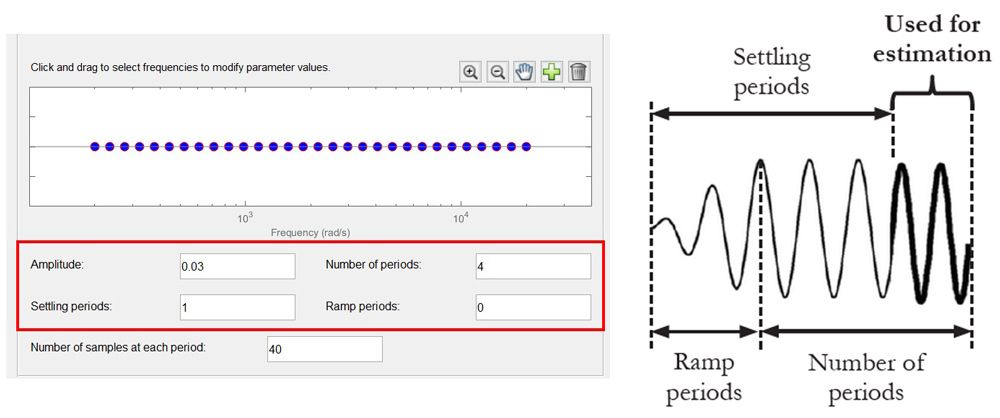
接下来，我们可以针对全部或部分频率，指定振幅、周期数、斜坡周期数以及趋稳周期数（图 5）。
图 5. sinestream 信号的参数选择（左）和相应的实现结果（右）。
4. 计算非参数化频率响应。
要开始计算，单击 Estimate 选项卡上的 Estimate 按钮。在仿真运行的同时，Simulink Control Design 在我们指定的输入端注入 sinestream 信号，并在输出端测量响应。仿真结束时，该 App 的工作区中将创建一个 frd 对象。此对象收集频率响应数据，即非参数化模型，它以离散的频率点描述系统。图 6 显示时域和频域结果。
图 6. 时域和频域的仿真结果。
5. 获得参数化模型
在此步骤中，我们使用 System Identification Toolbox™ 中的 tfest 命令，对数据进行传递函数拟合，即提取 idtf 对象表示的参数化模型。为此，我们需要将之前得到的 frd 对象从 Linear Analysis 工作区复制到 MATLAB 工作区（如图 6 红色箭头所示）。接下来，可以在命令行或脚本中使用 tfest 命令。由于 Boost 变换器是二阶系统，因此，需要将 tfest 中的极数设为 2。如果不知道要估计动态的系统是几阶，我们可以尝试几个不同的极数值，并选择拟合较为理想的最低值。
6. 验证结果。
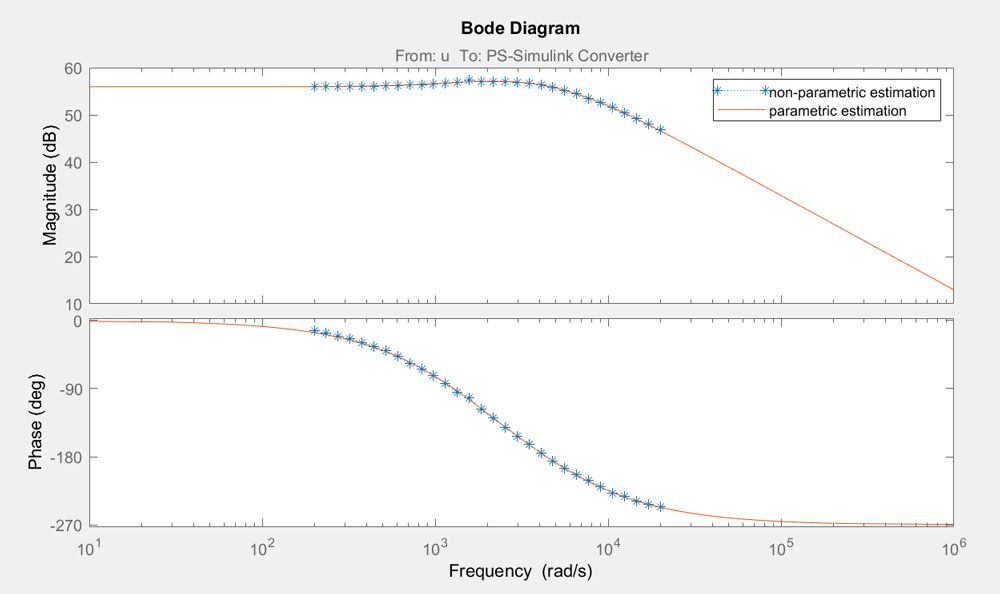
首先，在连续传导模式 (CCM) 下验证 Boost 变换器的参数化和非参数化估计。图 7 显示这两个估计相当吻合。
图 7. 非参数化和参数化估计的波特图。
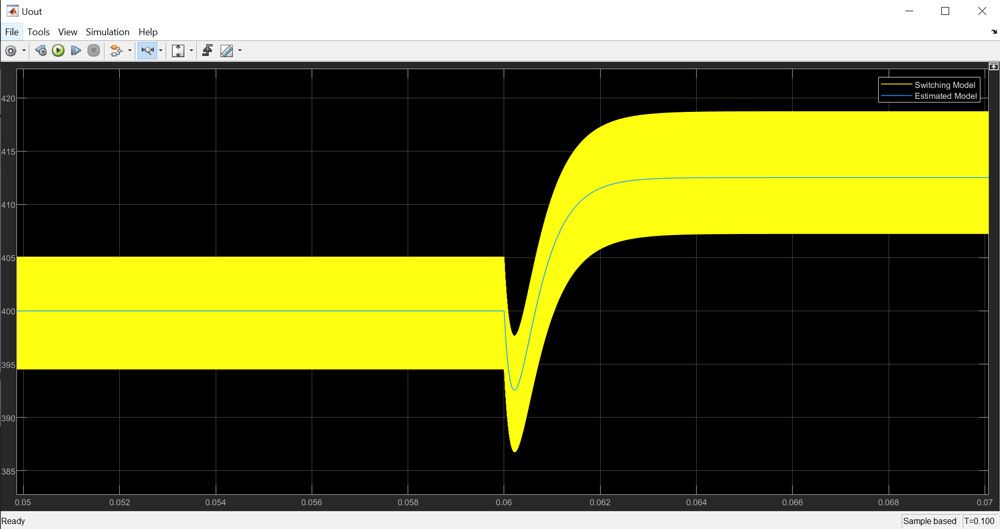
接下来，在 Simulink® 环境中，使用开关模式 Boost 变换器和用于实现参数化估计的 Transfer Function 模块进行仿真，以执行时域验证。我们测量并比较两个系统对同一个小扰动信号（即在稳态占空比上迭加的 2% 正阶跃）的响应。图 8 显示估计模型响应与开关模型响应十分接近，证实了该估计的有效性。
图 8. 时域验证呈现了开关模型和估计模型对同一个小扰动信号的响应。
现在，我们计算得出了 Boost 变换器模型的 LTI 表示，接着就可以利用它来进行控制设计和分析。具体来说，我们可以将估计的 LTI 对象导入 PID Tuner，以便调节控制器参数，从而满足带宽、相位裕度和其他反馈动态要求。
2020年发布
