Configure Custom Modulation Schemes for 6G

Since R2025a

This example uses:

6G Exploration Library for 5G Toolbox 6G Exploration Library for 5G Toolbox

This example shows how to use custom modulation to explore 6G candidate modulation schemes.

Introduction

6G Exploration Library for 5G Toolbox™ enables you to modulate waveforms using constellations beyond the list specified in TS 38.211 Section 5.1 [1]. The library enables you to use any constellation, provided its number of points is a positive integer power of 2.

Generate Cross QAM Constellation

Use the qammod function to generate a 32-QAM constellation. TS 38.211 Section 5.1 lists only constellations that have even modulation order. Therefore, 5G Toolbox™ does not support this constellation because its modulation order is 5. Constellations like this are called cross QAM because they are shaped like a cross in the I/Q plane.

crossQAM = qammod(0:31,32,UnitAveragePower=true);

Create a physical downlink shared channel (PDSCH) configuration object, specifying custom modulation. Specify the constellation as the 32-QAM constellation you generated. Display a scatter plot of the constellation.

pdsch = pre6GPDSCHConfig(Modulation="Custom",Constellation=crossQAM);
scatterplot(pdsch.Constellation)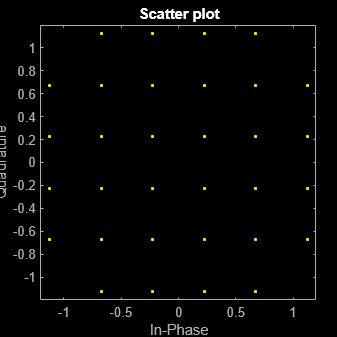

Figure Scatter Plot contains an axes object. The axes object with title Scatter plot, xlabel In-Phase, ylabel Quadrature contains a line object which displays its values using only markers. This object represents Channel 1.

Generate Circular Constellations

This example generates a series of circular constellations and compares their performance with that of standard QAM and cross QAM constellations. Specifically, the example analyzes the peak to average power ratios (PAPRs) and the bit error ratios (BERs). The example analyzes PAPRs both before and after discrete Fourier transform spread OFDM (DFT-s-OFDM) modulation.

Specify modulation orders 2 through 12 in a vector.

modOrders = 2:12;

For each modulation order, generate the corresponding circular and standard constellations and return the number of symbols.

[circConsts,numSymbols] = getCircConsts(modOrders);
strdConsts = getStrdConsts(modOrders);

Update the PDSCH configuration object and display a scatter plot of the 32-point circular constellation.

pdsch.Constellation = circConsts{4};
scatterplot(pdsch.Constellation)

Calculate PAPRs Before Transmission

Get the PAPR for each circular constellation. In this case, the PAPR is equal to the peak power because the constellations have unit average power.

paprCirc = zeros(numel(modOrders),1);
for i=1:numel(modOrders)
    paprCirc(i) = max(abs(circConsts{i}).^2);
end

Get the PAPRs for the standard square and cross QAM constellations with orders 2 through 12.

paprStrd = zeros(numel(modOrders),1);
for i = 1:numel(modOrders)
    paprStrd(i) = max(abs(strdConsts{i}).^2);
end

Transmit PDSCH Waveforms

Specify the transmission parameters.

constInd = 2;                                                                 % Constellation index: modulation order 5
pdschCirc = pre6GPDSCHConfig(Modulation="Custom",PRBSet=0:274);               % PDSCH object for circular constellation
pdschCirc.Constellation = circConsts{constInd};

pdschStrd = pre6GPDSCHConfig(Modulation="Custom",PRBSet=0:274);               % PDSCH object for standard constellation
pdschStrd.Constellation = strdConsts{constInd};

pdsch = {pdschCirc,pdschStrd};
carrier = pre6GCarrierConfig(NSizeGrid=275);                                  % Carrier configuration
nTxAnts = 1;                                                                  % Use one transmit antenna
txDFTsOFDM = cell(1,2);

Create a resource grid for the carrier and transmit antenna.

txGrid = hpre6GResourceGrid(carrier,nTxAnts);

For the circular and standard constellation:

Get the data symbol indices for the carrier and PDSCH configurations.
Create PDSCH symbols for a random codeword and populate the resource grid.
Transform precode the PDSCH symbols for DFT-s-OFDM modulation.
Perform OFDM modulation.
Normalize the time-domain waveform to its maximum absolute value.

for i = 1:2
    [ind,indinfo] = hpre6GPDSCHIndices(carrier,pdsch{i});
    cw = randi([0 1],indinfo.G,1);
    txSym = hpre6GPDSCH(carrier,pdsch{i},cw);
    txGrid(ind) = txSym;
    txGrid = transformPrecode(pdsch{i},txGrid,ind);
    txWaveform = hpre6GOFDMModulate(carrier,txGrid);
    txDFTsOFDM{i} = txWaveform/max(abs(txWaveform),[],"all");
end

Calculate Bit Error Ratios

Now specify a signal-to-noise ratio (SNR) of 20 dB and calculate the corresponding noise variance.

snr = 20;
nVar = db2pow(-snr);
rxSym = cell(1,2);
refConst = cell(1,2);
errCirc = zeros(numel(modOrders),1);
errStrd = zeros(numel(modOrders),1);
errors = {errCirc,errStrd};
consts = {circConsts,strdConsts};
pdsch = pre6GPDSCHConfig(Modulation="Custom");

Compare the BERs for the circular and standard constellations. For each modulation order, follow these processing steps:

Generate a PDSCH waveform with a random codeword and the corresponding circular constellation.
Pass the waveform through an AWGN channel.
Get soft bits by decoding the received PDSCH symbols.
Convert the soft bits to hard bits and use the biterr function to get the bit error ratio.
Repeat steps 1 through 4 for the standard constellation with the same modulation order.

for constInd = 1:numel(modOrders)
    for i = 1:2
        pdsch.Constellation = consts{i}{constInd};
        [~,indinfo] = hpre6GPDSCHIndices(carrier,pdsch);
        cw = randi([0 1],indinfo.G,1);
        tx = hpre6GPDSCH(carrier,pdsch,cw);
        rx = awgn(tx,snr);

        if constInd == 4                                                        % Extract order 5 constellation for plotting
            rxSym{i} = rx;
            refConst{i} = pdsch.Constellation;
        end

        [cwEst,~] = hpre6GPDSCHDecode(carrier,pdsch,rx,nVar);
        cwEst = cwEst{1} < 0;
        errors{i}(constInd) = biterr(cw,cwEst)/numel(cw);
    end
end

Plot the received symbols for the 32-point cross QAM and circular constellations.

for i = 1:2
    cd = comm.ConstellationDiagram(ReferenceConstellation=refConst{i}, ...
    ShowReferenceConstellation=true);
    cd(rxSym{i})
end

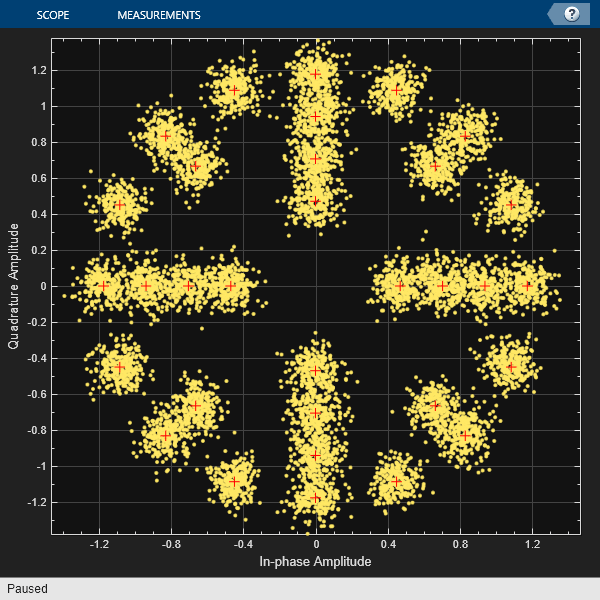
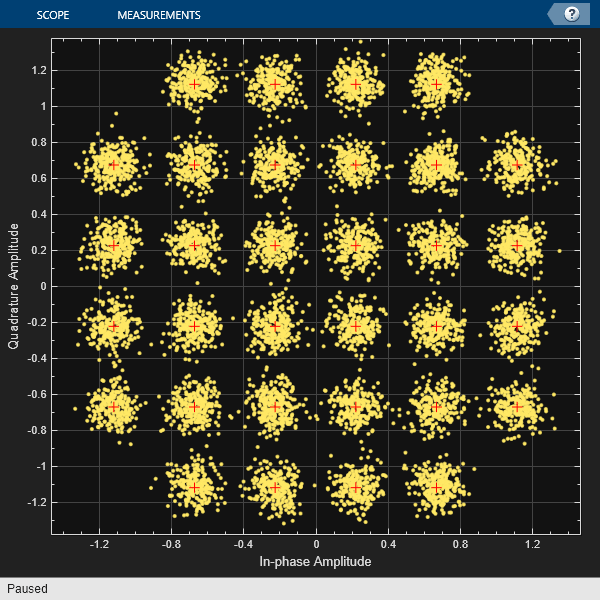
Plot PAPRs Before Transmission

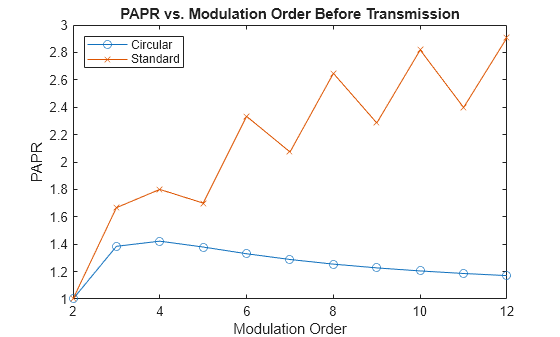
Plot the pretransmission PAPRs against the modulation order for the circular and standard constellations.

figure;
plot(modOrders,paprCirc,"-o")
hold on
plot(modOrders,paprStrd,"-x")
title("PAPR vs. Modulation Order Before Transmission")
xlabel("Modulation Order")
ylabel("PAPR")
legend("Circular","Standard",Location="northwest")

Figure contains an axes object. The axes object with title PAPR vs. Modulation Order Before Transmission, xlabel Modulation Order, ylabel PAPR contains 2 objects of type line. These objects represent Circular, Standard.

Calculate and Plot CCDF

Create a powermeter System object™, setting ComputeCCDF to true. This setting specifies that the System object computes the complementary cumulative distribution function (CCDF) of the power of the input signal. This CCDF shows the probability of a time-domain sample being a certain amount above the average power of the waveform. The CCDF of the power is a probabilistic analogue of the PAPR.

pm = powermeter(ComputeCCDF=true);

Measure and plot the CCDFs of the received DFT-s-OFDM waveforms for the circular and standard constellations.

pm(txDFTsOFDM{1});
figure;
plotCCDF(pm);
hold on
reset(pm);
pm(txDFTsOFDM{2});
plotCCDF(pm);
title("CCDF Comparison of DFT-s-OFDM Waveforms for Modulation Order 3");
legend("Circular","Standard");

Figure contains an axes object. The axes object with title CCDF Comparison of DFT-s-OFDM Waveforms for Modulation Order 3, xlabel Relative power (dB above average power), ylabel Probability (%) contains 2 objects of type line. These objects represent Circular, Standard.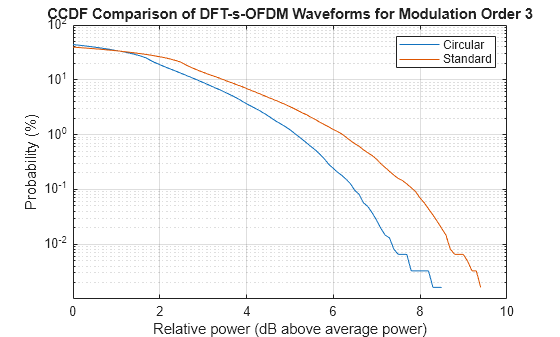

Plot BERs

Plot the BERs against the modulation orders for the circular and standard constellations. The circular constellations perform worse than the standard ones because the minimum distance between the constellation points is smaller, which makes them more susceptible to noise.

f = figure;
plot(modOrders,errors{1},"-o")
hold on
plot(modOrders,errors{2},"-x")
title("BER vs. Modulation Order")
xlim([2 12])
xlabel("Modulation Order")
ylabel("Bit Error Ratio")
legend("Circular","Standard",Location="northwest")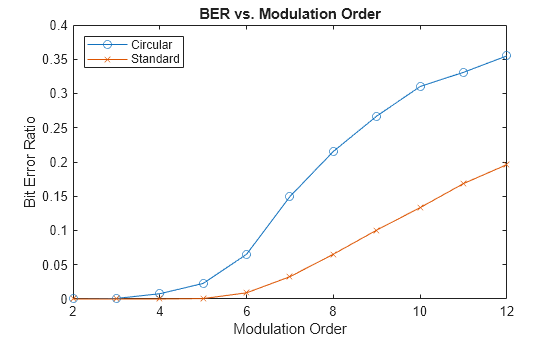

Figure contains an axes object. The axes object with title BER vs. Modulation Order, xlabel Modulation Order, ylabel Bit Error Ratio contains 2 objects of type line. These objects represent Circular, Standard.

References

[1] 3GPP TS 38.211 "NR; Physical channels and modulation" 3rd Generation Partnership Project; Technical Specification Group Radio Access Network.

Local Functions

function [constellations,numSymbols] = getCircConsts(orders)
    % Generate circular constellations and return numbers of symbols for given modulation orders

    numSymbols = 2.^orders;
    firstPoints = exp(1i .* 2*pi./numSymbols);
    amplitudes = 1.5:0.5:6;
    unitPoints = cell(numel(numSymbols),1);

    for i = 1:numel(numSymbols)
        range = 1:numSymbols(i);
        unitPoints{i} = firstPoints(i).^range;
        unitPoints{i} = unitPoints{i}';
    end

    constellations = cell(numel(numSymbols),1);
    constellations{1} = unitPoints{1};

    for i = 1:numel(numSymbols)-1
        constellations{i+1} = [constellations{i};amplitudes(i)*unitPoints{i}];
    end

    % Normalize to unit average power
    for i = 1:numel(numSymbols)
        constellations{i} = constellations{i}/rms(constellations{i});
    end
end

function constellations = getStrdConsts(orders)
    % Generate standard constellations for given modulation orders

    numSymbols = 2.^orders;
    constellations = cell(numel(numSymbols),1);

    for i = 1:numel(numSymbols)
        constellations{i} = qammod(0:numSymbols(i)-1,numSymbols(i), ...
        UnitAveragePower=true);
    end
end

function slotGrid = transformPrecode(pdsch,slotGrid,pdschInd)
    % Perform transform precoding for DFT-s-OFDM

    sym = slotGrid(pdschInd);    
    MRB = numel(pdsch.PRBSet);
    tp = nrTransformPrecode(sym,MRB);
    slotGrid(pdschInd) = tp;
end