SADEA Optimization of Six-Element Yagi-Uda Antenna using Custom Objective Function
This example shows how to optimize an antenna design using a custom objective function. The radiation patterns of antennas depend sensitively on the parameters that define the antenna shapes. Typically, the features of a radiation pattern have multiple local optima. The radiation pattern of the antenna is calculated using the pattern function in Antenna Toolbox. The optimization is performed using the optimize method which uses the SADEA optimizer for antennas and a custom objective function.
A Yagi-Uda antenna is a widely used radiating structure for a variety of applications in commercial and military sectors. This antenna can receive TV signals in the VHF-UHF range of frequencies [1]. The Yagi-Uda is a directional traveling-wave antenna with a single driven element, usually a folded dipole or a standard dipole, which is surrounded by several passive dipoles. The passive elements form the reflector and director. These names identify the positions relative to the driven element. The reflector dipole is behind the driven element, in the direction of the back lobe of the antenna radiation. The director dipole is in front of the driven element, in the direction where a main beam forms.
Design Parameters
Specify the initial design parameters for the Yagi-Uda antenna to operate at the center of the VHF band [2].
freq = 165e6;
wirediameter = 19e-3;
c = physconst("lightspeed");
lambda = c/freq;
Z0 = 300;
BW = 0.05*freq;
fmin = freq - 2*(BW);
fmax = freq + 2*(BW);
Nf = 101;Create Yagi-Uda Antenna
The driven element for the Yagi-Uda antenna is a folded dipole, a standard exciter for this type of antenna. Adjust the length and width parameters of the folded dipole. Because cylindrical structures are modeled as equivalent metal strips, calculate the width using the cylinder2strip utility function available in the Antenna Toolbox™. The length is at the design frequency.
d = dipoleFolded; d.Length = lambda/2; d.Width = cylinder2strip(wirediameter/2); d.Spacing = d.Length/60;
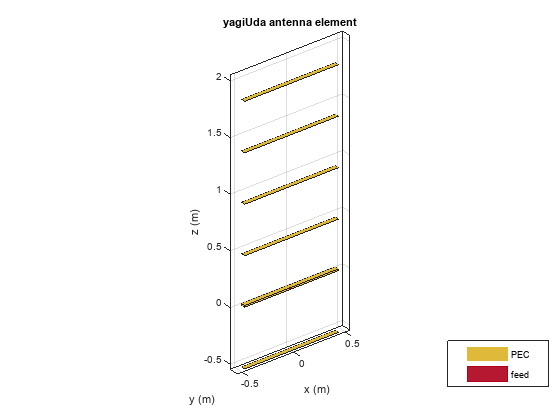
Create a Yagi-Uda antenna with the exciter as the folded dipole. Set the lengths of the reflector and director elements to be . Set the number of directors to four. Specify the reflector and director spacing as and , respectively. These settings provide an initial guess and serve as a starting point for the optimization procedure. View the initial design.
Numdirs = 4; refLength = 0.5; dirLength = 0.5*ones(1,Numdirs); refSpacing = 0.3; dirSpacing = 0.25*ones(1,Numdirs); initialdesign = [refLength dirLength refSpacing dirSpacing].*lambda; yagidesign = yagiUda; yagidesign.Exciter = d; yagidesign.NumDirectors = Numdirs; yagidesign.ReflectorLength = refLength*lambda; yagidesign.DirectorLength = dirLength.*lambda; yagidesign.ReflectorSpacing = refSpacing*lambda; yagidesign.DirectorSpacing = dirSpacing*lambda; fig = figure; show(yagidesign)
Plot Radiation Pattern at Design Frequency
Prior to executing the optimization process, plot the radiation pattern for the initial guess in 3-D.
fig1 = figure; pattern(yagidesign,freq);
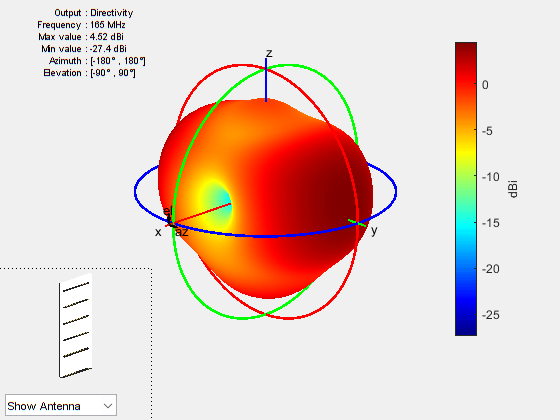
This antenna does not have a higher directivity in the preferred direction, at zenith (elevation = 90 deg). This initial Yagi-Uda antenna design is a poorly designed radiator.
Set Up Optimization
Use the following variables as control variables for the optimization:
Reflector length (1 variable)
Director lengths (1 variables)
Reflector spacing (1 variable)
Director spacings (1 variables)
The SADEA optimizer sets the values to the corresponding properties of the yagiuda and provides the antenna object as input to the custom objective function.
Create a custom objective function that takes the antenna as input and returns an objective value / penalty as output. The antenna is provided as input to the custom objective by the SADEA optimizer the parameters for the current iteration are set by the optimizer and given as input to the function. The custom objective function aims to have a large value in the 90-degree direction, a small value in the 270-degree direction, and a large value of maximum power between the elevation beamwidth angle bounds.
In addition to the directivity goal an impedance match condition is also included as a constraint. Any constraint violations will penalize the objective.
type yagi_custom_objective_function.mfunction objectivevalue = yagi_custom_objective_function(y,fc,Z0, BW, fmin, fmax, Nf, freq, ang, constraints)
% yagi_custom_objective_function returns the objective for a 6-element Yagi
% objectivevalue = yagi_custom_objective_function(y)
% it calculates the objective value for the yagiUda antenna y passed in as
% input by the SADEA optimizer
% The yagi_custom_objective_function function is used for an internal example.
% Its behavior might change in subsequent releases, so it should not be
% relied upon for programming purposes.
% Copyright 2023-2024 The MathWorks, Inc.
% Unpack constraints
Gmin = constraints.Gmin;
Gdev = constraints.Gdeviation;
FBmin = constraints.FBmin;
S11min = constraints.S11min;
K = constraints.Penalty;
% Calculate antenna port and field parameters
output = analyzeAntenna(y,fc,BW,ang,Z0);
% Form objective function
output1 = output.MaxDirectivity+output.MismatchLoss; % Directivity/Gain at zenith
% Gain constraint, e.g. G > 10
c1 = 0;
if output1<Gmin
c1 = Gmin-output1;
end
% Gain deviation constraint, abs(G-Gmin)<0.1;
c1_dev = 0;
if abs(output1-Gmin)>Gdev
c1_dev = -Gdev + abs(output1-Gmin);
end
% Front to Back Ratio constraint, e.g. F/B > 15
c2 = 0;
if output.FB < FBmin
c2 = FBmin-output.FB;
end
% Reflection Coefficient, S11 < -10
c3 = 0;
if output.S11 > S11min
c3 = -S11min + output.S11;
end
% Form the objective + constraints
objectivevalue = -output1 + max(0,(c1+c1_dev+c2+c3))*K;
end
function output = analyzeAntenna(ant,fc,BW,ang,Z0)
%ANALYZEANTENNA calculate the objective function
% OUTPUT = ANALYZEANTENNA(Y,FREQ,BW,ANG,Z0) performs analysis on the
% antenna ANT at the frequency, FC, and calculates the directivity at the
% angles specified by ANG and the front-to-back ratio. The reflection
% coefficient relative to reference impedance Z0, and impedance are
% computed over the bandwidth BW around FC.
fmin = fc - (BW/2);
fmax = fc + (BW/2);
Nf = 5;
freq = unique([fc,linspace(fmin,fmax,Nf)]);
fcIdx = freq==fc;
s = sparameters(ant,freq,Z0);
Z = impedance(ant,fc);
az = ang(1,:);
el = ang(2,:);
Dmax = pattern(ant,fc,az(1),el(1));
Dback = pattern(ant,fc,az(2),el(2));
% Calculate F/B
F_by_B = Dmax-Dback;
% Compute S11 and mismatch loss
s11 = rfparam(s,1,1);
S11 = max(20*log10(abs(s11)));
T = mean(10*log10(1 - (abs(s11)).^2));
% Form the output structure
output.MaxDirectivity= Dmax;
output.BackLobeLevel = Dback;
output.FB = F_by_B;
output.S11 = S11;
output.MismatchLoss = T;
output.Z = Z;
end
Set bounds on the control variables.
refLengthBounds = [0.4;
0.6].*lambda;
dirLengthBounds = [0.35 ; % lower bound on director length
0.5].*lambda; % upper bound on director length
refSpacingBounds = [0.05; % lower bound on reflector spacing
0.30].*lambda; % upper bound on reflector spacing
dirSpacingBounds = [0.05 ; % lower bound on director spacing
0.23].*lambda; % upper bound on director spacing
LBUB = {refLengthBounds(1) dirLengthBounds(1) refSpacingBounds(1) dirSpacingBounds(1);
refLengthBounds(2) dirLengthBounds(2) refSpacingBounds(2) dirSpacingBounds(2) };Define variables and constraints.
fc = 165e6; Z0 = 300; BW = 0.05*fc; fmin = fc - 2*(BW); fmax = fc + 2*(BW); Nf = 101; freq = linspace(fmin,fmax,Nf); ang = [0 0;90 -90]; constraints.S11min = -10; constraints.Gmin = 10.5; constraints.Gdeviation = 0.1; constraints.FBmin = 15; constraints.Penalty = 50;
Define function handle for custom objective.
customObjectiveFcnHandle = @(y)yagi_custom_objective_function(y, fc ,Z0, BW, fmin, fmax, Nf, freq, ang, constraints);
SADEA Optimization Using Custom Objective
Run the optimization using SADEA. Setup design variables as ReflectorLength, DirectorLength, ReflectorSpacing, DirectorSpacing. Set the number of iterations to 150. Call the optimize function on the Yagi-Uda antenna at the frequency defined by freq, with the previously specified options.
designVars = {'ReflectorLength','DirectorLength','ReflectorSpacing','DirectorSpacing'};
num_iterations = 150;
fig2 = figure;
optimdesign = optimize(yagidesign,fc,customObjectiveFcnHandle,designVars,LBUB,Iterations=num_iterations);
The optimization stopped because it completed the specified number of iterations.
Get the initial objective value.
initialObjectiveValue = customObjectiveFcnHandle(yagidesign)
initialObjectiveValue = 2.5898e+03
Get the final objective value.
finalObjectiveValue = customObjectiveFcnHandle(optimdesign)
finalObjectiveValue = 35.5791
Initial objective value of the antenna is around 2600. SADEA optimization has reduced the objective value to a much smaller value.
Plot Optimized Pattern
Plot the optimized antenna pattern at the design frequency.
yagidesign = optimdesign; fig3 = figure; pattern(yagidesign,fc)
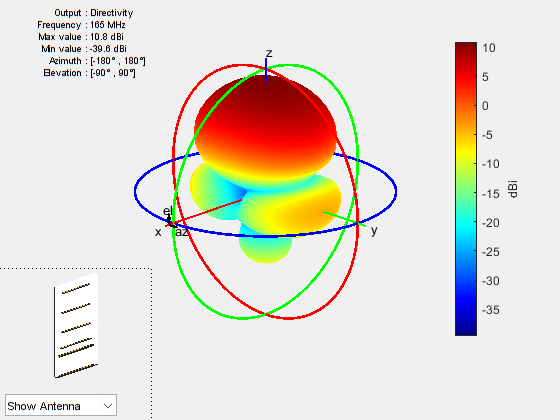
Apparently, the antenna now radiates significantly more power at zenith.
E-Plane and H-Plane Cuts of Pattern
To obtain a better insight into the behavior in two orthogonal planes, plot the normalized magnitude of the electric field in the E-plane and H-plane, that is, azimuth = 0 and 90 deg, respectively.
fig4 = figure; pattern(yagidesign,fc,0,0:1:359);
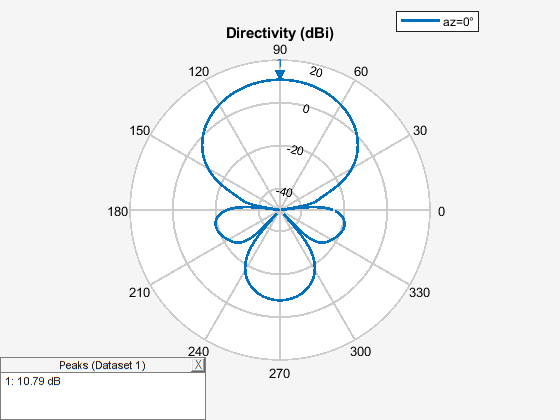
fig5 = figure; pattern(yagidesign,fc,90,0:1:359);
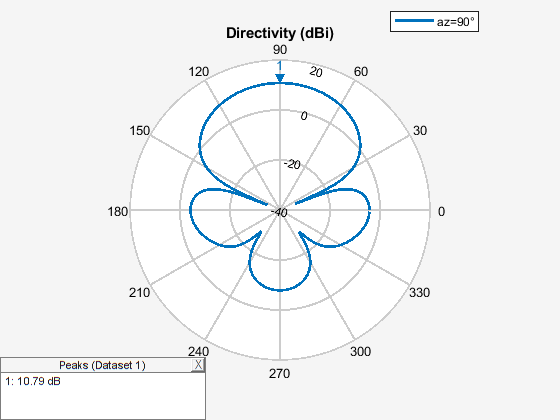
The optimized design shows a significant improvement in the radiation pattern. Higher directivity is achieved in the desired direction toward zenith. The back lobe is small, resulting in a good front-to-back ratio for this antenna. Calculate the directivity at zenith, front-to-back ratio, and beamwidth in the E-plane and H-plane.
D_max = pattern(yagidesign,fc,0,90)
D_max = 10.2407
D_back = pattern(yagidesign,fc,0,-90)
D_back = -18.1548
F_B_ratio = D_max - D_back
F_B_ratio = 28.3955
Eplane_beamwidth = beamwidth(yagidesign,fc,0,1:1:360)
Eplane_beamwidth = 52.0000
Hplane_beamwidth = beamwidth(yagidesign,fc,90,1:1:360)
Hplane_beamwidth = 64.0000
Input Reflection Coefficient of Optimized Antenna
Choose initial design parameters for the Yagi-Uda antenna to operate at the center of the VHF band [2]. The datasheet lists a 50Ω input impedance after taking a balun into the account. The model in this example does not account for the presence of the balun and therefore matches to the typical folded dipole input impedance of 300Ω.
freqRange = linspace(fmin,fmax,Nf); s = sparameters(yagidesign,freqRange,Z0); fig6 = figure; rfplot(s);
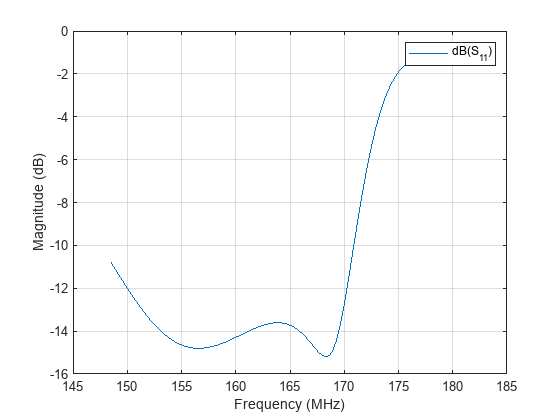
Comparison with Manufacturer Data Sheet
The optimized Yagi-Uda antenna achieves a forward directivity greater than 10 dBi, which translates to a value greater than 8 dBd (relative to a dipole). This is close to the gain value reported by the datasheet (8.5 dBd). The F/B ratio is13 dB which is slightly less than desired. The optimized Yagi-Uda antenna has a E-plane and H-plane beamwidth that compare favorably to the datasheet listed values of 52 degrees and 64 degrees respectively. The design achieves a good impedance match to , and has a -10 dB bandwidth of approximately 10%.
datasheetparam = {'Gain (dBi)';'F/B';'E-plane Beamwidth (deg.)';'H-plane Beamwidth (deg.)';'Impedance Bandwidth (%)'};
datasheetvals = [10.5,16,54,63,10]';
optimdesignvals = [D_max,F_B_ratio,Eplane_beamwidth,Hplane_beamwidth,10]';
Tdatasheet = table(datasheetvals,optimdesignvals,RowNames=datasheetparam)Tdatasheet=5×2 table
datasheetvals optimdesignvals
_____________ _______________
Gain (dBi) 10.5 10.241
F/B 16 28.395
E-plane Beamwidth (deg.) 54 52
H-plane Beamwidth (deg.) 63 64
Impedance Bandwidth (%) 10 10
Tabulate Initial and Optimized Design Parameters
Tabulate the initial design guesses and the final optimized design values.
yagiparam= {'Reflector Length';
'Director Length - 1'; 'Director Length - 2';
'Director Length - 3'; 'Director Length - 4';
'Reflector Spacing'; 'Director Spacing - 1';
'Director Spacing - 2'; 'Director Spacing - 3';
'Director Spacing - 4'};
initialdesignVal = initialdesign';
optimdesignVal = [optimdesign.ReflectorLength optimdesign.DirectorLength optimdesign.ReflectorSpacing optimdesign.DirectorSpacing]';
Tgeometry = table(initialdesignVal,optimdesignVal,RowNames=yagiparam)Tgeometry=10×2 table
initialdesignVal optimdesignVal
________________ ______________
Reflector Length 0.90846 0.94442
Director Length - 1 0.90846 0.7785
Director Length - 2 0.90846 0.69856
Director Length - 3 0.90846 0.78896
Director Length - 4 0.90846 0.77165
Reflector Spacing 0.54508 0.33471
Director Spacing - 1 0.45423 0.17612
Director Spacing - 2 0.45423 0.21252
Director Spacing - 3 0.45423 0.31208
Director Spacing - 4 0.45423 0.32787
Reference
[1] Balanis, Constantine A. Antenna Theory: Analysis and Design. Fourth edition. Hoboken, New Jersey: Wiley, 2016.
[2] “Yagi Antennas S.6Y-165.” Accessed July 3, 2024. https://amphenolprocom.com/products/base-station-antennas/2450-s-6y-165.
See Also
Objects
Functions
cylinder2strip|optimize|pattern|beamwidth|sparameters|rfplot