Main Content

permutationInvariantSISNR

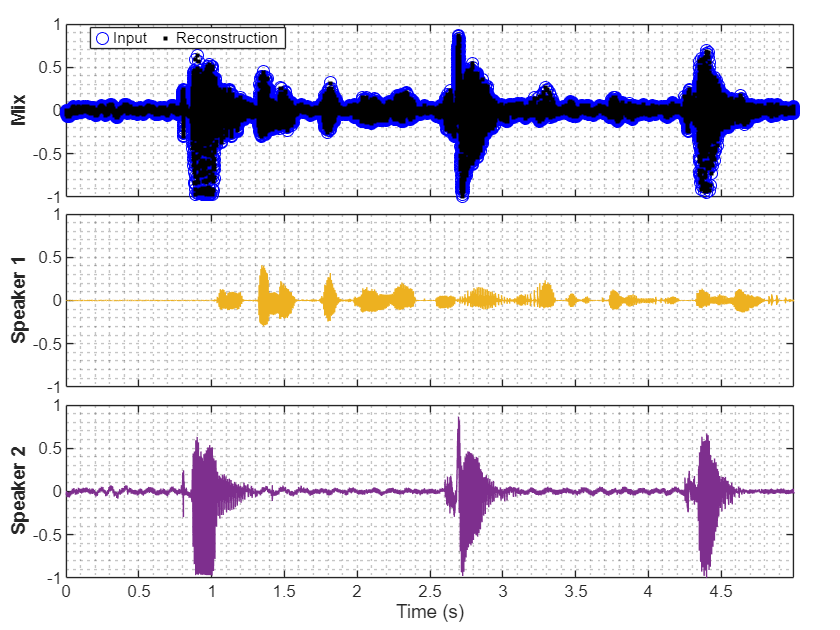
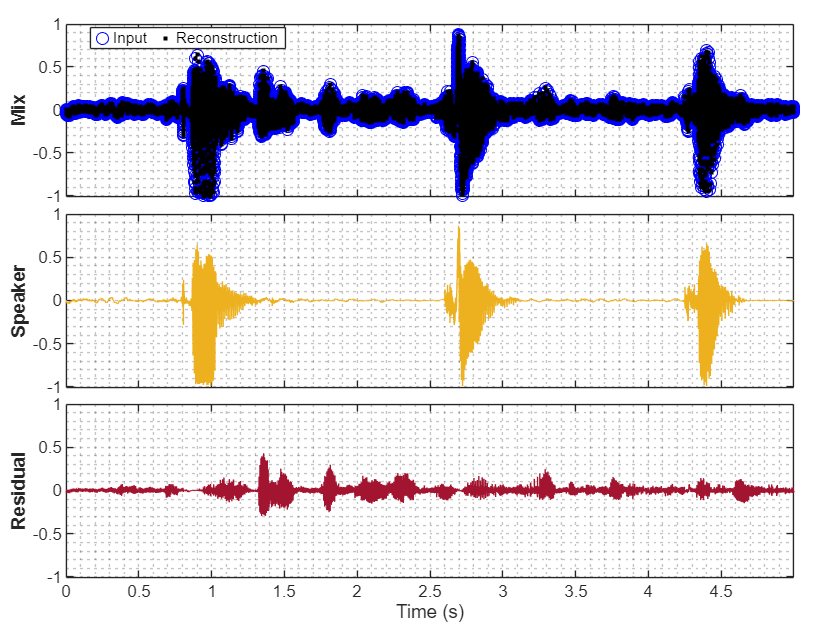
Permutation invariant SI-SNR

Since R2024b

collapse all in page

    Syntax

    metric = permutationInvariantSISNR(proc,ref)
    metric = permutationInvariantSISNR(proc,ref,Name=Value)
    [metric,refOrder] = permutationInvariantSISNR(___)

    Description

    metric = permutationInvariantSISNR(proc,ref) returns the scale-invariant signal-to-noise ratio (SI-SNR) using the ordering of reference signals that yields the optimal value for the given processed signals. This metric is invariant to the permutation of the reference signals, and you can therefore use it to evaluate a signal separation system without needing the order of the ground truth signals to align with the system output.

    example

    metric = permutationInvariantSISNR(proc,ref,Name=Value) specifies options using one or more name-value arguments. For example, permutationInvariantSISNR(proc,ref,SubtractMean=false) does not subtract the means from individual signals before computing the permutation invariant SI-SNR.

    example

    [metric,refOrder] = permutationInvariantSISNR(___) also returns the order of reference signals used to calculate the best SI-SNR.

    example

    Examples

    collapse all

    Open Live Script

    Create an audio signal that combines the speech of two speakers. Scale one of the speech signals by one half before summing them.

    [s,fs] = audioread("MultipleSpeakers-16-8-4channel-5secs.flac");
s = s(:,1:2).*[1,0.5];
x = sum(s,2);
x = x./max(abs(x));

    Use separateSpeakers to perform speaker separation on the mixed signal. Call the function again with no output arguments to plot the separated signals.

    y = separateSpeakers(x,fs,NumSpeakers=2);

separateSpeakers(x,fs,NumSpeakers=2)

    Figure contains 3 axes objects. Axes object 1 with ylabel Mix contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Input, Reconstruction. Axes object 2 with ylabel Speaker 1 contains an object of type line. Axes object 3 with xlabel Time (s), ylabel Speaker 2 contains an object of type line.

    Measure the SI-SNR to evaluate the speaker separation. Call sisnr comparing the separated signals with both possible permutations of the ground truth signals.

    snr1 = mean(sisnr(y,s))
    snr1 = single

-39.8843

    snr2 = mean(sisnr(y,fliplr(s)))
    snr2 = single

21.1212

    Use permutationInvariantSISNR to measure the SI-SNR of the best permutation aligning the separated signals with the ground truth.

    pi_snr = permutationInvariantSISNR(y,s)
    pi_snr = single

21.1212
    Open Live Script

    Create an audio signal that combines the speech of three speakers with different scaling factors.

    [s,fs] = audioread("MultipleSpeakers-16-8-4channel-5secs.flac");
s = s(:,1:3).*[1,0.5,0.1];
x = sum(s,2);
x = x./max(abs(x));

    Use separateSpeakers with NumSpeakers set to 1 to perform one-and-rest speaker separation on the mixed signal. Call the function again with no output arguments to plot the separated signals.

    [y,r] = separateSpeakers(x,fs,NumSpeakers=1);

separateSpeakers(x,fs,NumSpeakers=1)

    Figure contains 3 axes objects. Axes object 1 with ylabel Mix contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Input, Reconstruction. Axes object 2 with ylabel Speaker contains an object of type line. Axes object 3 with xlabel Time (s), ylabel Residual contains an object of type line.

    Measure the permutation invariant SI-SNR of the separated signal and residual with PermutationType set to "OR-PIT".

    proc = [y r];
pi_snr = permutationInvariantSISNR(proc,s,PermutationType="OR-PIT")
    pi_snr = single

18.1792

    Call permutationInvariantSISNR again with an additional output argument to get the index of the reference signal used as the "one" signal to calculate the SI-SNR. Use this index to listen to the signal.

    [~,refOrder] = permutationInvariantSISNR(proc,s,PermutationType="OR-PIT")
    refOrder = 
1

    groundTruthSeparatedSpeaker = s(:,refOrder);
sound(groundTruthSeparatedSpeaker,fs)

    Input Arguments

    collapse all

    Processed signal, specified as a column vector of length T, a T-by-N matrix, or a T-by-N-by-M array, where T corresponds to time, N is the number of signals in an example, and M is the number of examples to evaluate.

    You can specify proc as a dlarray (Deep Learning Toolbox). If the dlarrary is unformatted, it must have the same shape as previously described for regular numeric arrays. If the dlarrary is formatted, its dimensions must be 'SCBT', 'SBT', 'CBT', 'BT', 'SCT', 'ST', 'CT', or 'TU'. The 'T' dimension corresponds to T, and 'B' corresponds to M. If the format has both 'S' and 'C', one must be singleton and the other corresponds to N. The 'U' dimension must be singleton, so 'TU' corresponds to a column array.

    The size of the time dimension T must be equal to the time dimension of ref. If they are not equal, the function throws a warning and trims the longer signals so that they are equal before computing the SI-SNR.

    The number of examples M must be equal to the number of examples in ref.

    If PermutationType is "OR-PIT", N must equal 2, where the first signal is the "one" signal and the second signal is the "rest". If PermutationType is "uPIT", N must be equal to the number of signals in ref.

    Data Types: single | double

    Reference signal, specified as a column vector of length T, a T-by-N matrix, or a T-by-N-by-M array, where T corresponds to time, N is the number of signals in an example, and M is the number of examples to evaluate.

    You can specify ref as a dlarray (Deep Learning Toolbox). If the dlarrary is unformatted, it must have the same shape as previously described for regular numeric arrays. If the dlarrary is formatted, its dimensions must be 'SCBT', 'SBT', 'CBT', 'BT', 'SCT', 'ST', 'CT', or 'TU'. The 'T' dimension corresponds to T, and 'B' corresponds to M. If the format has both 'S' and 'C', one must be singleton and the other corresponds to N. The 'U' dimension must be singleton, so 'TU' corresponds to a column array.

    The size of the time dimension T must be equal to the time dimension of proc. If they are not equal, the function throws a warning and trims the longer signals so that they are equal before computing the SI-SNR.

    The number of examples M must be equal to the number of examples in proc.

    If PermutationType is "uPIT", N must be equal to the number of signals in proc.

    Data Types: single | double

    Name-Value Arguments

    Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

    Example: permutationInvariantSISNR(proc,ref,SubtractMean=false)

    Type of permutation invariance, specified as "uPIT" or "OR-PIT".

    • "uPIT" — Calculate the permutation invariant SI-SNR for utterance-level permutation invariant training (uPIT). The number of signals N in proc and ref must be equal.

    • "OR-PIT" — Calculate the permutation invariant SI-SNR for one-and-rest permutation invariant training (OR-PIT). The number of signals N in proc must be equal to 2, but ref can have more than 2 signals.

    For more information about uPIT and OR-PIT, see Permutation Invariant Training.

    Data Types: char | string

    Center all individual signals by subtracting the signal means before computing the SI-SNR.

    Data Types: logical

    Output Arguments

    collapse all

    Permutation invariant SI-SNR in dB, returned as a scalar with the same data type as the inputs. The metric is averaged across the M different examples in the inputs. For more information about the permutation invariant SI-SNR metric, see Algorithms.

    Indices of the optimal order of reference signals used to calculate the metric.

    If PermutationType is "uPIT", permutationInvariantSISNR returns refOrder as a 1-by-N-by-M array, where N is the number of signals and M is the number of examples in the inputs proc and ref. For each example m, ref(:,refOrder(:,:,m),m) returns the reference signals in the ordering that results in the optimal SI-SNR with proc(:,:,m).

    If PermutationType is "OR-PIT", permutationInvariantSISNR returns refOrder as a 1-by-1-by-M array, where M is the number of examples in the inputs proc and ref. For each example m, ref(:,refOrder(m),m) returns the "one" signal that results in the optimal SI-SNR for one-and-rest training with proc(:,:,m). All of the other reference signals summed together correspond to the "rest" signal.

    Algorithms

    collapse all

    SI-SNR

    The scale-invariant signal-to-noise ratio (SI-SNR) measures the level of distortion or noise in a processed signal by comparing it to a reference signal in a way that is invariant to the scaling of the signals. This metric is useful for evaluating speech enhancement and source separation systems.

    The permutationInvariantSISNR function calculates the SI-SNR according to the following formula, where s is the reference signal and ŝ is the processed signal.

    SI-SNR=10log10(‖αs‖2‖αs−s^‖2), where α=s^Ts‖s‖2

    By default, the permutationInvariantSISNR function subtracts the mean to zero-center the signal before calculating the SI-SNR. You can skip this step by setting SubtractMean to false, and the resulting metric is commonly referred to as the scale-invariant signal-to-distortion ratio (SI-SDR).

    Permutation Invariant Training

    Permutation invariant training is a method for training signal separation systems on data with examples containing a mixed signal and the ground truth separated reference signals. The training objective for these systems is to maximize the SI-SNR between the predicted separated signals and the ground truth. However, evaluating the SI-SNR requires labeling each predicted signal with a corresponding ground truth signal, and the correct correspondence is ambiguous since the system could output well-separated signals in multiple different permutations while still having good performance. Permutation invariant training solves this ambiguity by measuring the SI-SNR between the predicted signals and every possible permutation of the ground truth reference signals, then uses the best result to evaluate that training example. By maximizing this resulting permutation invariant SI-SNR metric, a system can learn to separate signals from the labeled data.

    The standard approach is to compute the permutation invariant SI-SNR on whole signals, as opposed to frame-level predictions, while training with a known number of separate signals. This approach is known as utterance-level permutation invariant training (uPIT). Alternatively, permutation invariant training can be used with one-and-rest signal separation, where a system is trained to take the mixed signal and output one separated signal along with the "rest" of the signal, which can be recursively fed back into the system to separate the other signals. This approach is known as one-and-rest permutation invariant training (OR-PIT). OR-PIT requires calculating the SI-SNR between the two predicted signals and each permutation of the ground truth references where one reference is chosen as the "one" signal and the others are summed to form the "rest" signal.

    For an example where you can train a speaker separation system using either uPIT or OR-PIT, see Train End-to-End Speaker Separation Model.

    References

    [1] Kolbaek, Morten, Dong Yu, Zheng-Hua Tan, and Jesper Jensen. “Multitalker Speech Separation With Utterance-Level Permutation Invariant Training of Deep Recurrent Neural Networks.” IEEE/ACM Transactions on Audio, Speech, and Language Processing 25, no. 10 (October 2017): 1901–13. https://doi.org/10.1109/TASLP.2017.2726762.

    [2] Takahashi, Naoya, Sudarsanam Parthasaarathy, Nabarun Goswami, and Yuki Mitsufuji. “Recursive Speech Separation for Unknown Number of Speakers.” In Interspeech 2019, 1348–52. ISCA, 2019. https://doi.org/10.21437/Interspeech.2019-1550.

    [3] Yu, Dong, Morten Kolbaek, Zheng-Hua Tan, and Jesper Jensen. “Permutation Invariant Training of Deep Models for Speaker-Independent Multi-Talker Speech Separation.” In 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 241–45. New Orleans, LA: IEEE, 2017. https://doi.org/10.1109/ICASSP.2017.7952154.

    Extended Capabilities

    GPU Arrays
    Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

    Version History

    Introduced in R2024b

    See Also

    |

    Topics